高级数据结构

树状数组

-->前置的一个知识lowbit

所谓lowbit就是一个数最低位的1所表示的数字大小

00001010

= 10

此时的lowbit是2不是第二位，而是2^1

lowbit (i)=2^i末尾0数量

lowbit可以用来判断在树状数组中一个数组元素包含原数组的个数

如7的lowbit是1，c[7]=a[7]（一个元素）;

如6的lowbit是2 ,c[6]=a[6]+a[5] (两个元素）;

单点修改，区间求和时

相对于普通数组O(1)修改，O(n)求和的时间复杂度

相对于前缀和数组O(n)修改，O(1)求区间的复杂的

它是O(logn)算法复杂度的修改，O(logn)求区间

int lowbit(i)
{

return i&-i;

}

单点更新

将下标为p的元素更新x

会更新所有包含p的树状数组

void add(long long p, long long x)
{

    while (p <= n)
    {
        c[p] += x;
        p += p & -p;
    }
}		

区间查询

区间求和

求从1-m的元素和

long long sum(long long m)
{
    long long s = 0;
    while (m > 0)
    {
        s += c[m];
        m -= m & -m;
    }
    return s;
}

区间相减

将1_{b的区间总和减去1}a-1

long long ask(long long a, long long b)

{

  return sum(b) - sum(a - 1);

}

[区间修改，单点查询]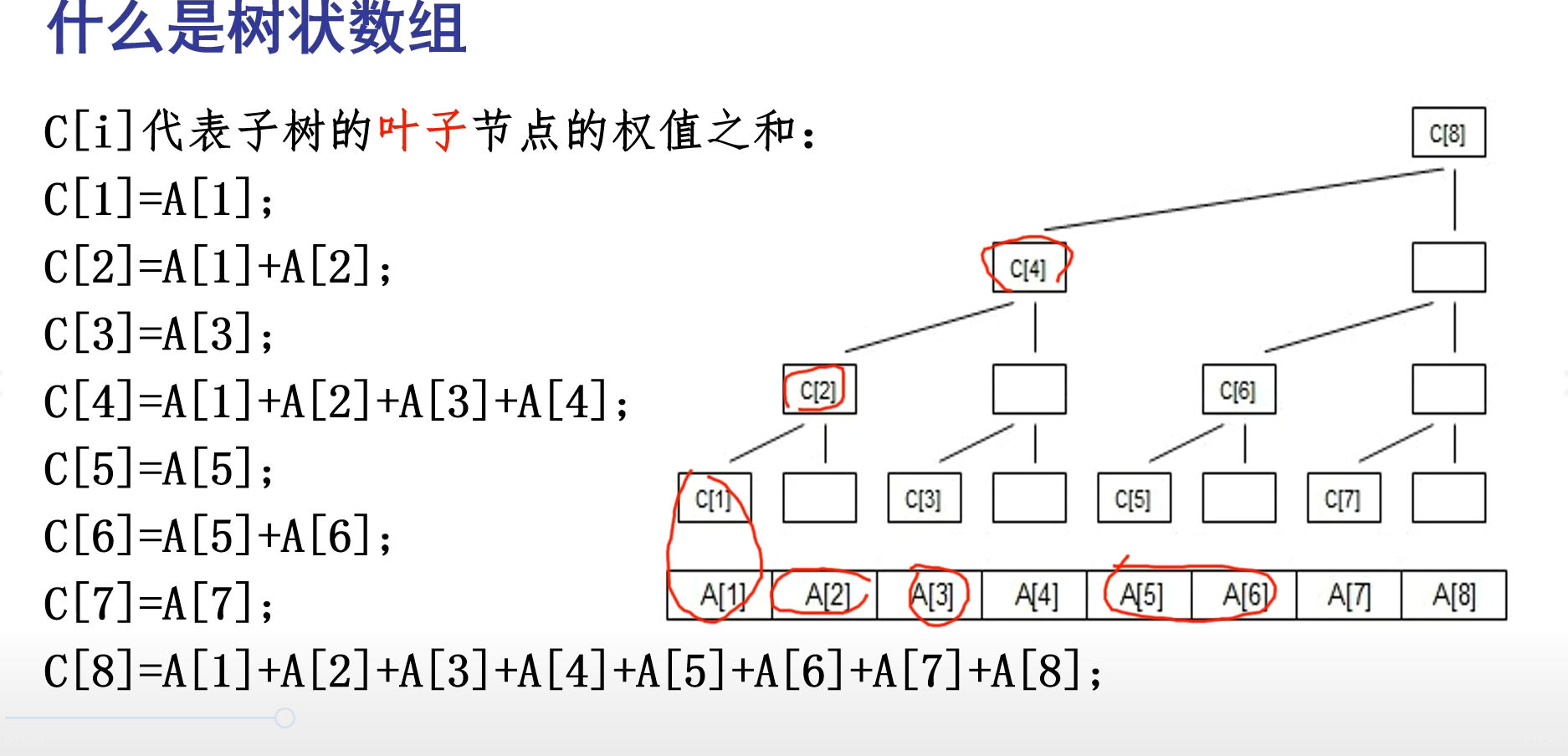

修改

使用差分数组

void update(int l, int r)
{
    d[l] += 1;
    d[r + 1] -= 1;
}

查询

设原数组为, 设数组，则，可以通过求的前缀和查询。

即d[i]的区间求和

[区间修改，区间查询](file:///E:/algorithm%20resource/%E6%9D%BF%E5%AD%90/%E6%A0%91%E7%8A%B6%E6%95%B0%E7%BB%84/Problem%20-%201006.html)

//更新下标为p的数组元素，更新x
//c1[i] c2[i] 分别是d[i] d[i]*i的树状数组
void add(int p, int x)
{
    for (int i = p; i <= n; i += i & -i)//含有C1[p]的树状数组都+x，含有c2[p]的树状数组都+x*p，因为d[p]+x后，d[p]*p会变大x*p
        c1[i] += x, c2[i] += x * p;
}
void update(int l, int r, int x)
{
    add(l, x);
    add(r + 1, -x);
}		//由于d[i]为差分数组，只要修改d[l]与，d[r+1]就行了
long long sum(int p)
{
    long long sum = 0;
    for (int i = p; i > 0; i -= i & -i)
        sum += (p + 1) * c1[i] - c2[i];

    return sum;
}
long long ask(int l, int r)
{
    return sum(r) - sum(l - 1);
}

\[\begin{equation*} S =\sum_{i=1}^p \sum_{j=1}^id[j]=\sum_{i=1}^pd[i]*(p-i+1)=(p+1)*\sum_{i=1}^pd[i]-\sum_{i=1}^pd[i]*i \end{equation*} \]

离散化

struct A
{
int index,value;
}a[maxn];

for(int i=1;i<=n;i++)
b[a[i].index]=i;//此时a已经按大小排序过了

线段树

不超过2logN条的原因是，由于区间是连续的，每次向上合并时结果也是连续的(未证明)

所以每当有3个子区间在同一层连续时，必然会有两个可以合并

此处的2logN指的是2(log(b-a+1)+1)

其中[1_{13]是该节点为原数组下标为1}13的元素值之和

![image-20210402100819946](C:\Users\10711\AppData\Roaming\Typora\typora-user-images\image-20210402100819946.png

//线段树的构造
struct segtrees
{
    int val;
}segtree[maxn<<2];
void pushup(int xb)//xb是节点下标
{
segtree[xb].val=segtree[xb<<1].val+segtree[xb<<1|1].val;
//指的是，当前下标为xb的节点值为xb*2+(xb*2+1)的值的和(见下图)
}
//从(1,n,1)开始
void build(int l,int r,int xb)
{
if(l==r)//当划分到一个区间只有一个元素时(叶子节点)
{
segtree[xb].val=a[l];
return ;
}
int m=(l+r)/2;//二分
build(l,m,xb*2)//向下传递，搜索区间二分后对应子区间的左边的区间
build(m+1,r,xb*2+1);//右子树
pushup(xb);//在执行这一句之前，xb的所有子节点都有了自己的值，即下标xb*2与xb*2+1值已求得
}

//线段树的更新a[L]+=C
//单点更新
//搜索O(logN),回溯更新O(logN)
//从(L,C,1,n,1)开始
int L,C;
void update(int l,int r,int xb)
{
if(l==r)
{
segtree[xb].val+=c;
return ;
}
int m=(l+r)>>1;
if(L<=m) update(l,m,xb<<1);
else update(m+1,r,xb<<1|1);
pushup(xb);
}

//区间查询
//值得一提的是，以下和以上的int可以酌情改为long long并最好是这个。
//[L,R]表示查询区间，[l,r]表示当前区间，xb表示当前区间下标
//l,r,xb与之构造的segtree对应，所以才能return segtree[xb].val;
int L,R;
int query(int l,int r,int xb)
{
   if(L<=l&&r<=R)
       return segtree[xb].val;//当前区间在要查询的范围内
    if(L>r||R<l)		//考虑了与所查询区间无关的可能性
    return 0;
    int m=(l+r)>>1；
    int ans=0;//以下是剪过枝的
    if(L<=m) ans+=query(l,m,xb<<1)；
    if(R>m) ans+=query(m+1,r,xb<<1|1);
	return ans;//以下好写
    //return query(l,m,xb<<1)+query(m+1,r,xb<<1|1);
}   

思考问题：线段树和树状数组的查询和修改不能统一的原因在于？

//区间更新
int L,R
void update(int l,int r,int rt)
{
    if(L<=l&&r<=R)	//判断当前区间是否在L,R里，若是则更新值并打下lazy符号
    {
        segtree[rt].val+=C*(r-l+1);
        segtree[rt].lazy+=C;
        return;
    }
	int m=(l+r)>>1;
    pushdown(rt,m-l+1,r-m);	//下推后更新子节点
    if(L<=m) update(l,m,rt<<1);
    if(R>m) update(m+1,r,rt<<1|1);
    pushup(rt);	//当子节点更新完后才更新当前节点
    
}

//区间更新下推
void pushdown(int rt,int ln ,int rn)
{
if(segtree[rt].lazy)
{
segtree[rt<<1].lazy+=segtree[rt].lazy;
segtree[rt<<1|1].lazy+=segtree[rt].lazy;
segtree[rt<<1].val+=segtree[rt].lazy*ln;
segtree[rt<<1|1].val+=segtree[rt].lazy*rn;
segtree[rt].lazy=0;
}
}

//区间更新的查询
int query(int l,int r, int rt)
{
if(L<=l&&r<=R)
return segtree[rt].val;

if(L>r||R<l)
return 0;
int m=(l+r)>>1;
pushdown(rt,m-l+1,r-m);
return query(l,m,rt<<1)+query(m+1,r,rt<<1|1);
}