暑期集训个人预备赛（1）G题 爆头 （hdu 1174）

空间中点到直线的距离推荐使用向量叉乘来计算

这个题解了半天结果我把空间中的平面公式当成直线公式来解了，枯惹；
留下了不学无术的眼泪，高数期末考试警告。
get:计算距离的新方法。

向量的叉乘公式
向量的叉乘公式

而使用正弦定理计算三角形面积公式
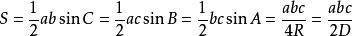
在这里插入图片描述
所以
向量的叉乘的模在几何上可以认为是求平行四边形的面积；
所以根据所求面积相等可知
设距离为d
d * | b | = |a x b|
好了，这个题解出来了。
下附此题代码

#include <bits/stdc++.h>

using namespace std;
double f(double x1,double y1,double z1,double x2,double y2,double z2)
{
    double x=(y1*z2-z1*y2);
    double y=(z1*x2-x1*z2);
    double z=(x1*y2-y1*x2);
    return sqrt(x*x+y*y+z*z)/sqrt(x2*x2+y2*y2+z2*z2);
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        double h1,r1,x1,y1,z1;
        double h2,r2,x2,y2,z2,x3,y3,z3;
        cin>>h1>>r1>>x1>>y1>>z1;
        cin>>h2>>r2>>x2>>y2>>z2>>x3>>y3>>z3;
        z2=h2*0.9-r2+z2;
        z1=h1-r1+z1;
        double x=x1-x2;
        double y=y1-y2;
        double z=z1-z2;
        double d=f(x,y,z,x3,y3,z3);
        if(d<=r1)
        {
            cout << "YES" <<endl;
        }
        else
        {
            cout << "NO" <<endl;
        }
    }
    return 0;
}

posted @ 2019-06-25 15:10  Voca  阅读(39)  评论(0)    收藏  举报