线段相交

预备

两个向量  和  的叉积写作 

由  和  

可得：

       当  时， 在  的逆方向。

       当  时， 在  的顺方向。

       当  时， 和  共线。

分析

快速排斥

两条线段分别为对角线构造矩形。

若这两个矩形不相交，则这两条线段肯定不相交。

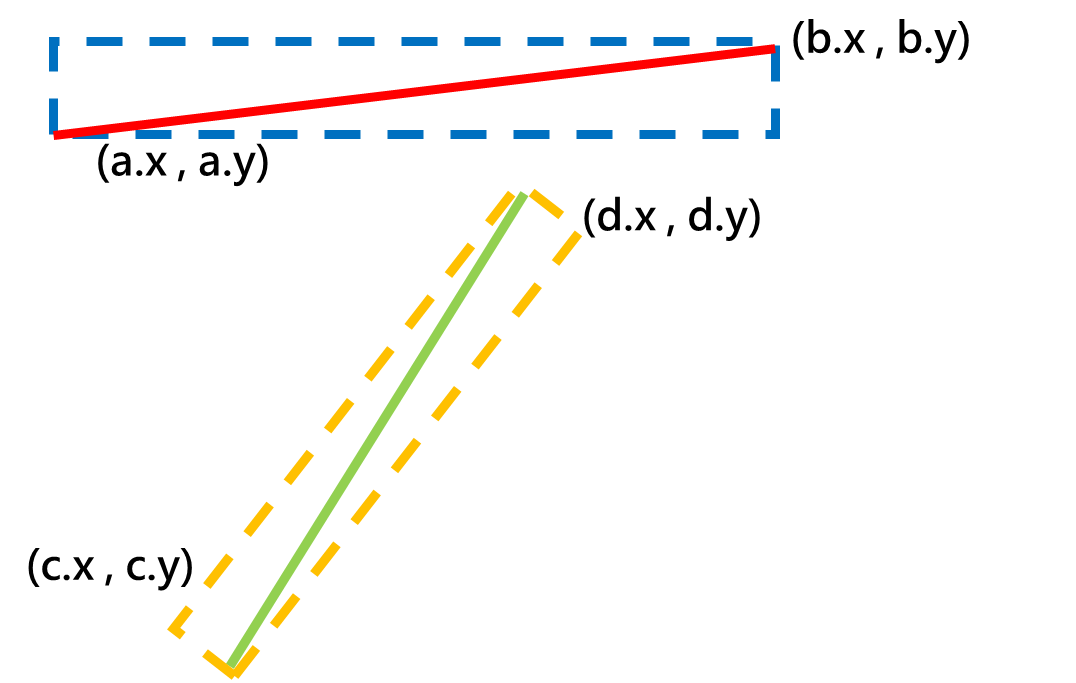
若这两个矩形相交，则需要跨立实验进一步判断。

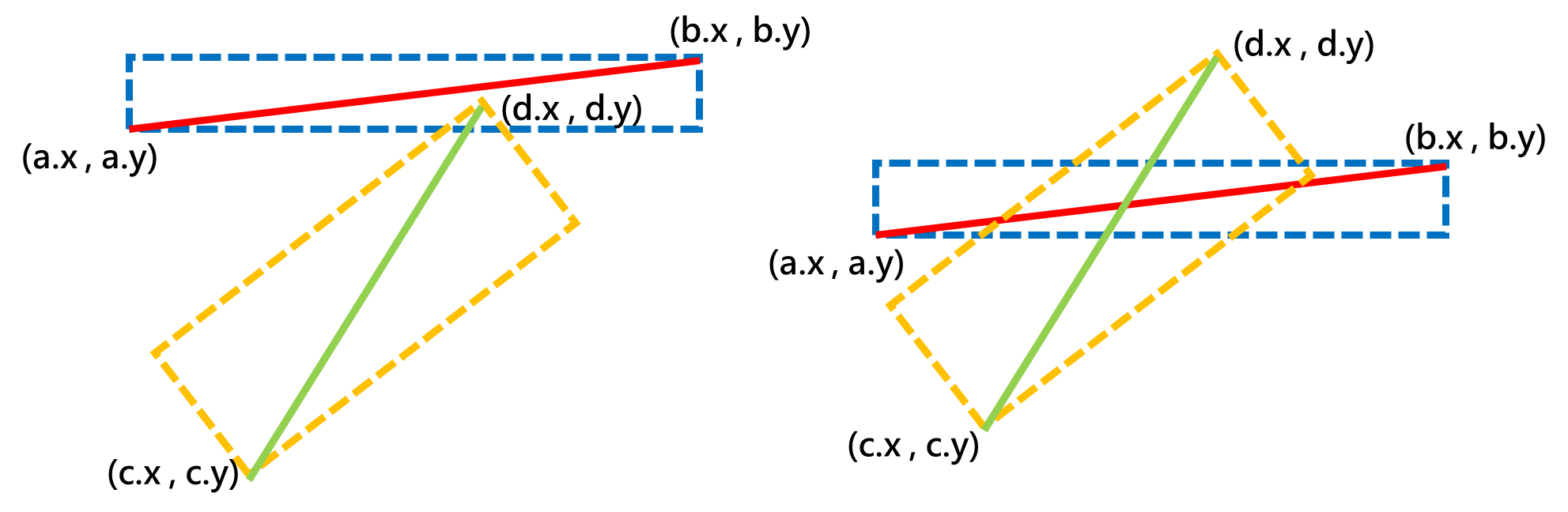
代码

if(max(a.x,b.x)<min(c.x,d.x)) return false;
if(max(a.y,b.y)<min(c.y,d.y)) return false;
if(max(c.x,d.x)<min(a.x,b.x)) return false;
if(max(c.y,d.y)<min(a.y,b.y)) return false;

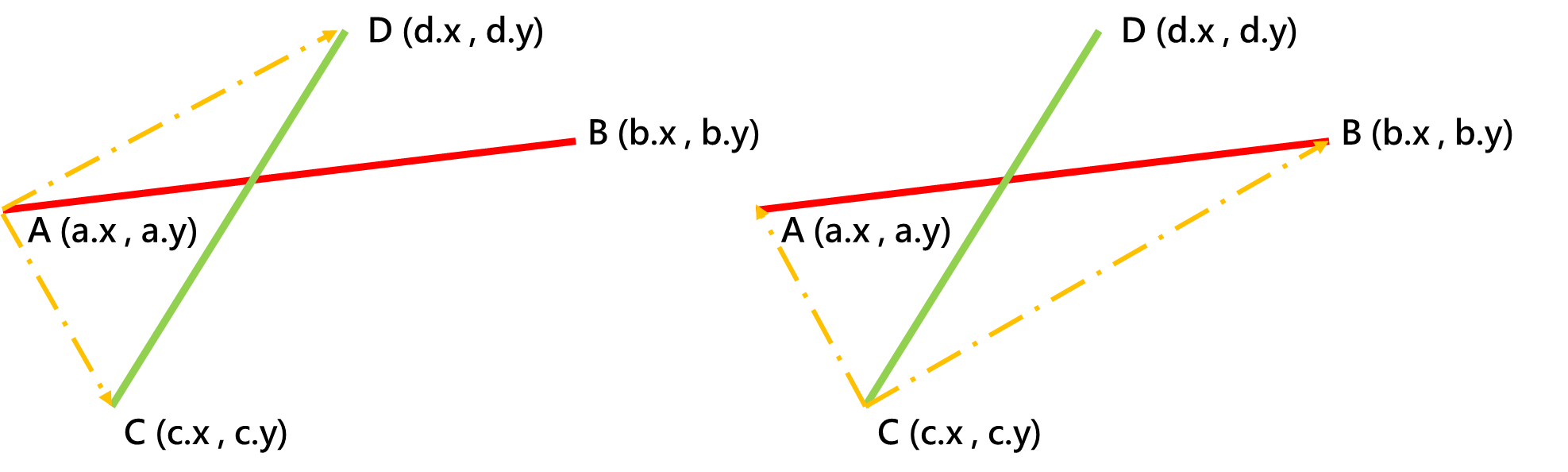
跨立实验

如果两条线段相交，那么 A 点，B 点肯定在线段 CD 两侧；同样，C 点，D 点肯定在线段 AB 两侧。

反之，若A 点，B 点在线段 CD 两侧；C 点，D 点在线段 AB 两侧，那么两条线段相交。

那么这时候可以利用叉积求解。

①  若 ，则可以得出在  两侧，即C 点，D 点在线段AB两侧。

②  若 ，则可以得出在  两侧，即A 点，B 点在线段CD两侧。

 

 

你会发现在条件① ②中，存在等于0的情况。这是为了处理两条线段只有一个点相交的情况。

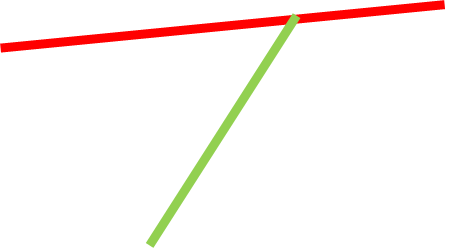
综上，当同时满足条件① ②时，两条线段相交。

特殊情况

 当 时，说明线段AB与CD平行。

随意取两条线段各一点，与任意一条线段做叉积：

    ① 若 ，则两线段共线。

    ② 若，则两线段平行。

代码

struct Point
{
  int x,y;
};
double mult(Point p0,Point p1,Point p2) 
{return (p1.x-p0.x)*(p2.y-p0.y)-(p1.y-p0.y)*(p2.x-p0.x);}
bool Judge(Point a,Point b,Point c,Point d)    
{
    if(max(a.x,b.x)<min(c.x,d.x)) return false;     
    if(max(a.y,b.y)<min(c.y,d.y)) return false;
    if(max(c.x,d.x)<min(a.x,b.x)) return false;
    if(max(c.y,d.y)<min(a.y,b.y)) return false;
    if(mult(a,c,b)*mult(a,b,d)<0) return false;  
    if(mult(c,a,d)*mult(c,d,b)<0) return false;
    return true;
}