机器学习速通入门

提要：

本文拟通过白话语言来粗浅介绍和讨论机器学习相关理念和算法，通过简单介绍概念、建立感性认知、利用现有学习库来实现初步机器学习对数据的处理和相应实践操作。

一.机器学习的基本认知

1.1机器学习的本质与分类

机器学习本质上是让模型从数据中自动学习规律。

以下是机器学习的分类和核心目标：

监督学习

对一个带标签的数据集进行分析，核心目标在于回归和预测。

比如垃圾邮件识别、车流预测、房价预估。

无监督学习

对一个无标签的数据集学习内在规律，核心目标在于聚类和降维。

比如用户分群，高维数据压缩等等。

其他类别

强化学习、半监督学习、集成学习等等，本文暂不讨论。

1.2机器学习的流程

机器学习有三大核心重点：数据，模型，算法。在完成一套机器学习流程时需要围绕这三个核心来进行。

1.2.1数据收集与处理

对于机器学习所用的数据，本文仅讨论格式化数据，如excel、csv等。

在获取数据后，需要对数据进行初步处理，否则难以用于模型。数据处理包含以下内容：

1.数据清洗：对缺失值、重复值、异常值的处理等等。

2.数据转换：格式统一、类型转换。

3.拆分数据集：分出训练集和测试集。按业务目标指定y。

4.特征工程：对数据的标准化和归一化、编码等。还包括对X的处理，比如去除无关特征。

1.2.2模型设置和建立

在上述针对数据的工作进行完毕之后，需要选择特定的模型对数据进行学习。

本文涉及的模型及算法如下：

监督学习：线性回归，岭回归，Lasso回归，多项式回归，逻辑回归，决策树，随机森林，SVM（支持向量机），KNN（K近邻），朴素贝叶斯

进阶优化：XGBoost、LightGBM、CatBoost

无监督学习：K-Means，PCA（主成分分析）

1.2.3模型评估

分类任务：准确率，精确率，召回率，F1-Score。

辅助：混淆矩阵，ROC-AUC

回归任务：MAE（平均绝对误差）、MSE（均方误差）、\(R^2\)(决定系数）

还包括交叉验证、消融实验、泛化能力检验等等。

二、机器学习的核心工作

2.1数据处理

2.1.1数据概览

# 打印数据集的形状（行数, 列数），方便我们了解有多少条样本和多少个特征
print(f"Dataset Shape: {train_df.shape}")

# 打印数据的基本信息，包括每一列的名称、数据类型、非空值数量等
# 可以帮助我们发现是否存在缺失值，以及每列的数据类型是否合理（如数字、字符串等）
print("\nData Info:")
train_df.info()

# 打印数值类型特征的汇总统计信息，如平均值、标准差、最大最小值、四分位数等
# 有助于快速了解数据的分布情况和是否存在异常值
print("\nNumerical Features Summary:")
display(train_df.describe())

# 显示数据集的前10行内容，便于我们快速了解每一列的数据长什么样
# 通常用于检查数据加载是否成功，以及观察数据格式是否正确
print("\nFirst 10 Rows of the Dataset:")
display(train_df.head(10))

2.1.2数据处理

对于有缺失值、重复值的数据可以用以下类似方法处理：

# 删除重复行
df = df.drop_duplicates()   

# 用众数填充所有列的缺失值
df = df.fillna(df.mode().iloc[0])          #iloc[0]代表出现多个众数时选择第一个众数

2.1.3绘图

绘图常常用来了解异常值情况、数据分布的大概模样以及观测特征重要性。以以下热力图为例：

# 计算数值特征之间的相关系数矩阵，反映特征之间的线性相关程度
correlation_matrix = train_df[numerical_features].corr()
# 创建新的图表，大小为 10x8 英寸
plt.figure(figsize=(10, 8))
# 使用 seaborn 的 heatmap 函数绘制相关系数热力图：
# - annot=True 显示每个单元格的数值
# - cmap="coolwarm" 使用蓝红色调表示相关性强弱（蓝色负相关，红色正相关）
# - fmt=".2f" 控制显示数值的小数点精度为两位
sns.heatmap(correlation_matrix, annot=True, cmap="coolwarm", fmt=".2f")
# 设置热力图标题
plt.title("Correlation Matrix of Numerical Features")
# 显示热力图
plt.show()

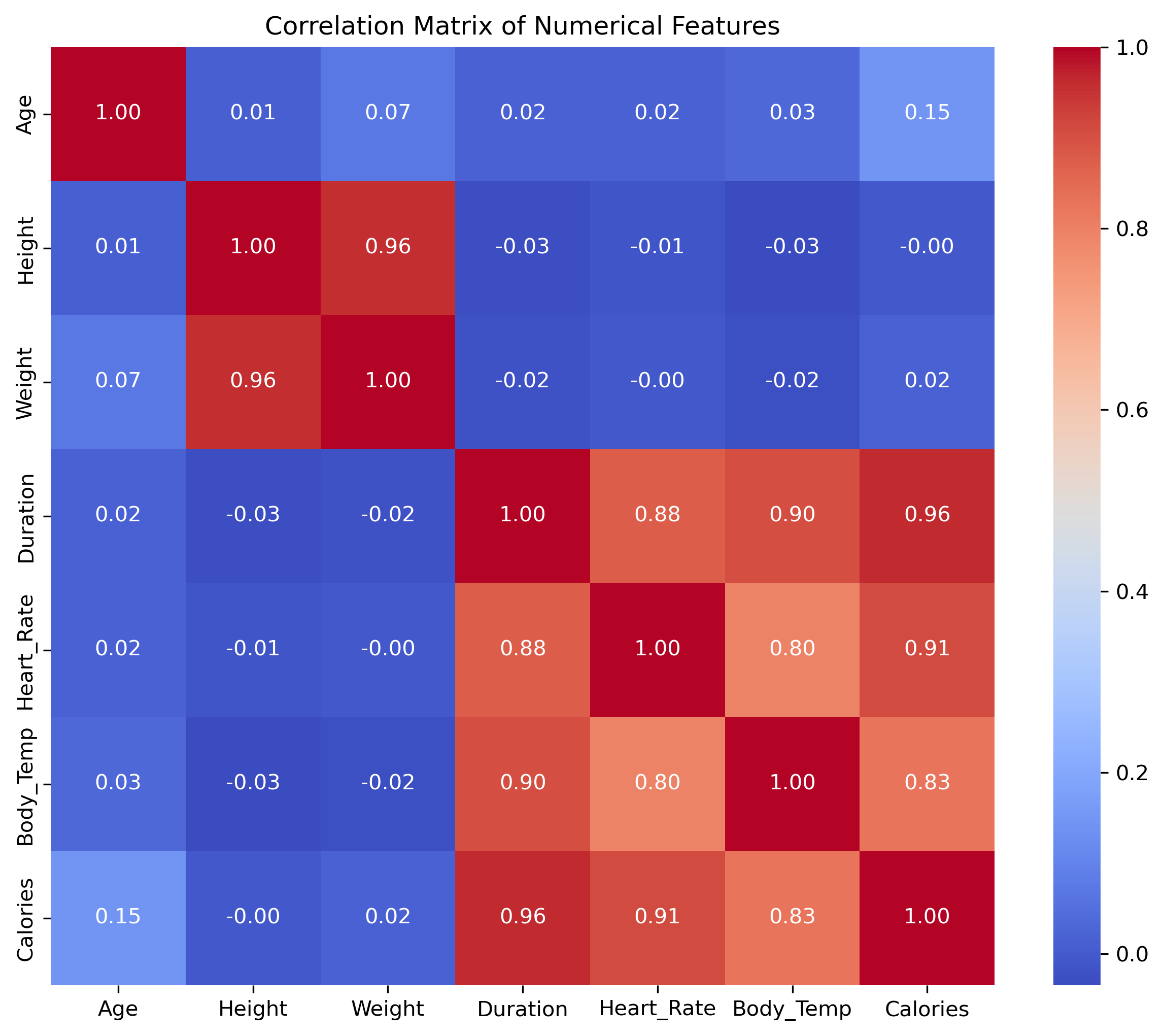
可以发现，该图极大的便捷特征工程工作，可以直观、快速挑选出核心变量。

2.2模型与算法

模型与算法为机器学习核心内容，本模块用白话阐述，旨在快速理解模型。

线性回归/岭回归/Lasso回归

用线性函数 \(y=wx+b\) 拟合已知数据，找到均方误差$ MSE = \frac{1}{m} \sum_{i=1}^{m} (y_i - \hat{y}_i)^2 $最小的线。

迭代过程主要在于通过学习率和梯度更新参数：$ w=w-αΔ $

岭回归和Lasso回归是在线性回归基础上添加正则项，旨在提升泛化性，避免过拟合。

正则化：给复杂模型惩罚，避免模型过于复杂。

逻辑回归

分类算法。基于线性回归的线性输出通过sigmoid函数（激活函数的一种）映射到[0,1]区间，变为事件发生的概率，再按阈值（通常为0.5）分类为正/反类。

决策树

本质是：基于问题做选择的树状流程图。逐步按照特征进行判断，最后落到结果。

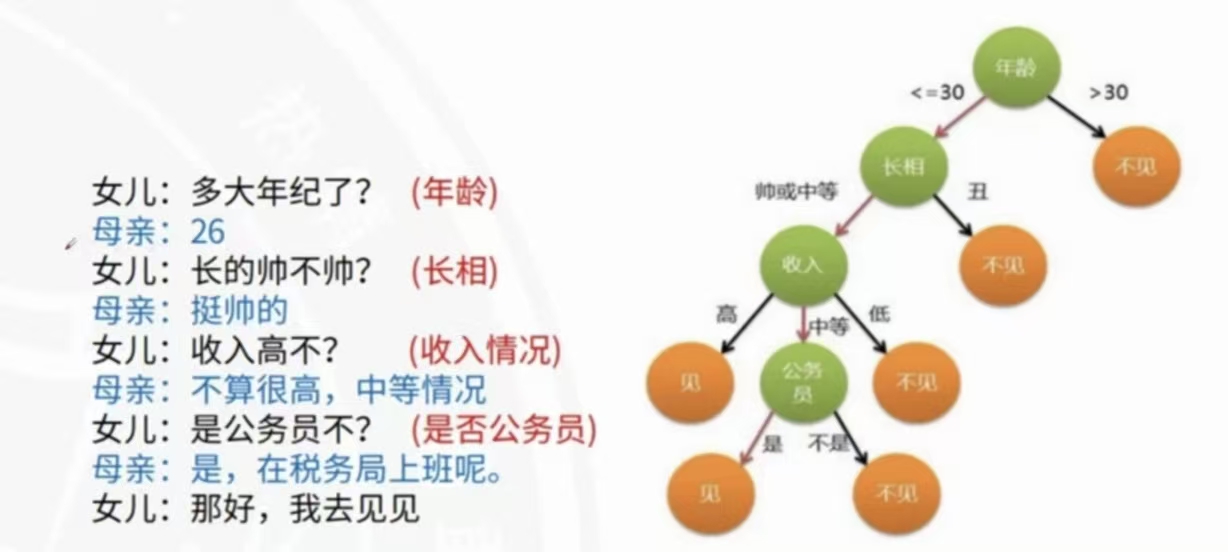
其中，常用CART算法，计算Gini（基尼系数）判断分类时的纯度，选择加权Gini最小的划分作为当前节点最佳划分属性。比如某个分类后，一个分支的叶子全是同一类就是最纯的，Gini为0。（杂的Gini趋近1）

随机森林

基于多棵决策树，通过：

样本随机性（有放回抽样原数据集得到样本）

特征随机性（选取特征时随机挑一小部分来用）

最终集成森林结果，比如平均或者众数来输出结果，优势较单棵决策树抗过拟合。

SVM（支持向量机）

找到最优超平面分类数据并使两个类别之间间隔最大化。

支持向量：离决策面最近、决定上下边界的关键点。

软间隔：允许有些点分错或者落在边界内，但总体间隔尽量大。

硬间隔：在所有数据点都能被完全正确分类的情况下找到最大间隔。

KNN（K近邻）

新样本的类别/数值由邻居投票决定。

算出新样本与所有样本的距离（常用欧式距离），选取最近的K个，然后按规则出结果。

分类：K个邻居中，哪个类别最多就选哪个类。

回归：K个邻居的标签平均值作为预测值。

朴素贝叶斯

分类模型。用概率论中的贝叶斯公式计算概率，选取概率最大的类。

XGBoost/LightGBM/CatBoost

基于梯度提升树（GBDT)，核心在于训练时串行训练，用下行的树通过预测前序模型的误差来弥补。

K-Means

聚类算法，随机选K个中心，然后样本归最近的中心成簇，然后算本次迭代后的中心更新中心坐标，如此重复。

PCA（主成分分析）

降维算法，找数据方差最大的方向（主成分），然后通过获取该方向上的投影，投影后维度变少，也保证保留一些信息。注意，降维后其他维度的信息可能值都会有变化。

2.3模型训练与调参

2.3.1基本训练过程

简易机器学习中，在数据处理完毕后的具体训练过程大多通过现有学习库来实现。步骤如下：

1.拆分数据集

# 先分出X和y列
y = data_np[:, 0]
X = data_np[:, 1:]
# 拆分数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=42)
# X_train为训练集特征
# y_train为训练集标签
# X_test为测试集特征
# y_test为测试集标签
# test_size=0.2   训练集:测试集==8:2
# random_state=42    随机种子，42为玩梗。

2.其他数据处理

对于类别型数据，可以用以下两种常见编码方式：

# 标签编码
label_encoded = le.fit_transform(['苹果','香蕉','苹果','橙子'])  
# 依照顺序赋值0，1，2.....
# 如本例，苹果为0，香蕉为1，橙子为2.

# 独热（one-hot）编码
dummies_Embarked = pd.get_dummies(data_train['Embarked'], prefix='Embarked', dtype=int)
# 将单列特征化为多列特征，属于某类的则在该类列下赋值为1，否则为0
# 需要合并到原数据中并删除原列

根据模型需要，做标准化和归一化。

# 标准化
from sklearn.preprocessing import StandardScaler
X_train_std = StandardScaler().fit_transform(X_train)
X_test_std = StandardScaler().transform(X_test)
# 归一化
from sklearn.preprocessing import MinMaxScaler
X_train_mm = MinMaxScaler().fit_transform(X_train)
X_test_mm = MinMaxScaler().transform(X_test)

注意，一定要先拆数据集再进行这类操作，否则会有数据泄露。

这些操作应对训练集进行，然后用该编码规则对测试集处理。

3.训练模型（逻辑回归为例）

# 导入逻辑回归模型
from sklearn.linear_model import LogisticRegression

# 初始化逻辑回归模型，设置随机种子和最大迭代次数
log_reg = LogisticRegression(random_state=0, max_iter=1000)

# 在训练数据上训练模型
log_reg.fit(X_train, y_train)

# 在测试数据上评估模型准确率
log_reg_score = log_reg.score(X_test, y_test)

# 打印逻辑回归模型的准确率
print("逻辑回归模型的准确率为 {:.2f}%".format(log_reg_score * 100))

4.评估模型

from sklearn.metrics import precision_score, recall_score, f1_score, roc_auc_score

# 预测测试集的标签
y_pred = log_reg.predict(X_test)

# 预测测试集的概率（用于计算ROC AUC）
y_prob = log_reg.predict_proba(X_test)[:, 1]

# 计算各项指标
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
roc_auc = roc_auc_score(y_test, y_prob)

print(f"Precision: {precision:.2f}")
print(f"Recall: {recall:.2f}")
print(f"F1 Score: {f1:.2f}")
print(f"ROC AUC: {roc_auc:.2f}")

2.3.2模型调参

比如KNN的邻居数、决策树的最大深度等等都称为超参数，超参数不被模型学习，而是提前被人为赋予，所以，挑选合理、高效的超参数是必要的。超参数的选取也有如下方法：

1.网格搜索（Grid Search）

# 定义待调优的参数网格
param_grid = {
    'penalty': ['l1', 'l2', 'elasticnet', None],  # 正则化类型：L1、L2、弹性网和无正则化
    'C': [0.01, 0.1, 1, 10, 100],                  # 正则化强度的倒数，值越小正则化越强
    'solver': ['lbfgs', 'liblinear', 'saga'],      # 求解器，不同的算法用来训练模型
    'max_iter': [500, 1000, 2000]                   # 最大迭代次数，避免训练时不收敛
}
# 初始化逻辑回归模型，这里不传参数，交给GridSearchCV去调参
log_reg = LogisticRegression(random_state=0)  # 设置随机种子保证结果可复现
# 创建GridSearchCV对象，进行参数搜索和交叉验证
grid_search = GridSearchCV(
    estimator=log_reg,           # 需要调参的模型
    param_grid=param_grid,       # 参数网格
    scoring='f1',                # 以F1分数作为评估指标，平衡准确率和召回率
    cv=5,                       # 5折交叉验证，保证模型稳定性
    #五折交叉验证是将训练集拆成五份，轮流用4份训练，1份测试，最终取5次得分均值。
    verbose=2,                  # 输出详细的训练进度信息
    n_jobs=-1                   # 使用所有CPU核加速计算
)

网格搜索将所有可能出现的超参数组合暴力枚举，用所有组合依次训练。如本例：

4 × 5 × 3 × 3 = 180 种

2.随机搜索（Randomized Search）

随机搜索会从给定的参数分布中，随机抽取指定次数（n_iter）的参数组合进行模型训练和评估，对每个组合训练模型并验证性能，最后选出最佳参数。

3.贝叶斯优化调参

# 定义参数搜索空间（注意参数类型和范围）
pbounds = {
    'n_estimators': (50, 300),    # 决策树数量
    'max_depth': (3, 20),         # 树的最大深度
    'min_samples_split': (2, 10)  # 拆分内部节点的最小样本数
}

# 初始化贝叶斯优化器并开始优化
optimizer = BayesianOptimization(
    f=rf_cv,          # 目标函数
    pbounds=pbounds,  # 参数空间
    random_state=42,
    verbose=2         # 打印优化过程（1=基本信息，2=详细信息）
)

# 开始迭代优化（n_iter=迭代次数，init_points=初始随机探索次数）
optimizer.maximize(init_points=5, n_iter=15)

# 输出最优参数和对应的得分
print("\n最优参数组合：", optimizer.max['params'])
print("五折交叉验证的最优平均得分：", optimizer.max['target'])

只需要给超参数的范围，该方法通过迭代优化选取超参数。

4.Optuna调参

# 创建一个研究对象，目标是最大化accuracy
study = optuna.create_study(direction='maximize')
# 运行超参数搜索，n_trials表示试验次数
study.optimize(objective, n_trials=50) # objective是目标函数

# 输出最优参数和对应的准确率
print("最佳参数:", study.best_params)
print(f"测试集最佳准确率: {study.best_value:.4f}")

同贝叶斯优化，给出超参数范围迭代优化。

2.3.3可解释性分析

SHAP可解释性分析方法如下：

# SHAP解释性分析
# 创建一个SHAP解释器，用于计算特征对模型输出的影响值（SHAP值）
explainer = shap.Explainer(model)

# 计算测试集X_test中每个样本的SHAP值
# shap_values是一个数组，表示每个特征对该样本预测结果的贡献
shap_values = explainer.shap_values(X_test)

# 绘制全局特征重要性图
shap.summary_plot(shap_values, X_test)

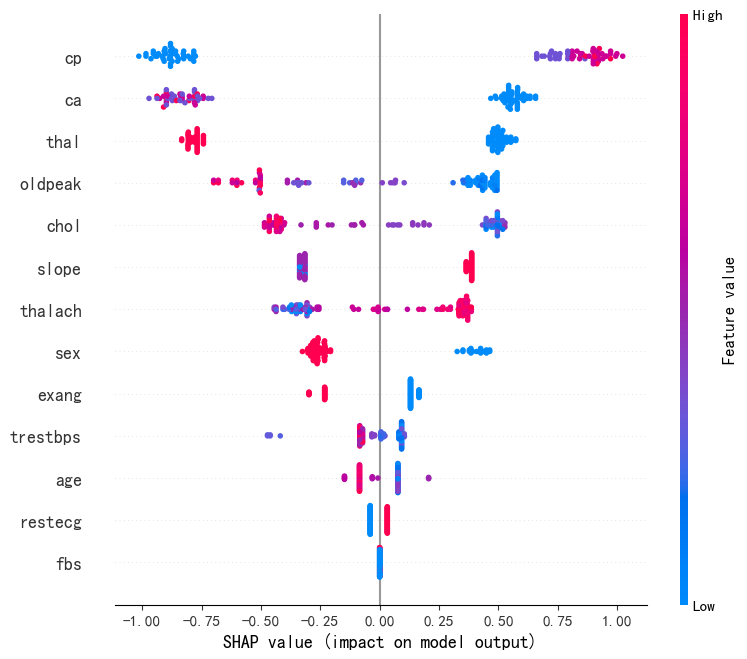
从图可读出每个特征对预测结果的贡献程度，红色代表该特征推高模型输出，蓝色代表该特征拉低模型输出。