主席树

主席树

主席树全称是可持久化权值线段树，即对权值开线段树，参见 知乎讨论。

引入

先引入一道题目：给定 \(n\) 个整数构成的序列 \(a\)，将对于指定的闭区间 \([l, r]\) 查询其区间内的第 \(k\) 小值。

你该如何解决？

一种可行的方案是：使用主席树。
主席树的主要思想就是：保存每次插入操作时的历史版本，以便查询区间第 \(k\) 小。

怎么保存呢？简单暴力一点，每次开一棵线段树呗。
那空间还不爆掉？

例如我们上面开了两个线段树，现在我们要在4的位置加上1：

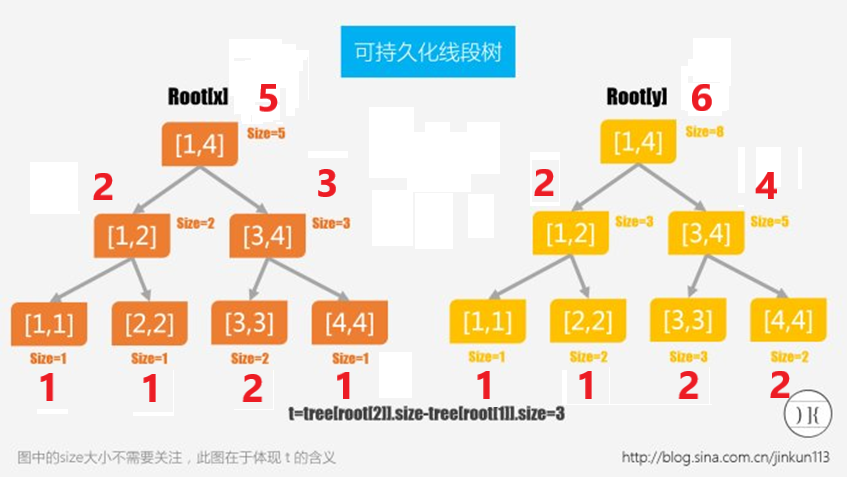
发现，我们每次只修改了一条链上的值，

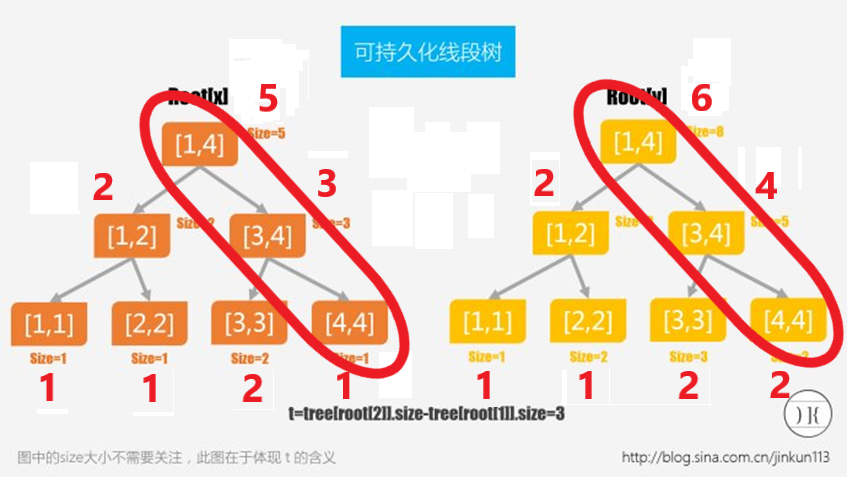
所以我们只需要多记录一条链就能代表历史的版本了：

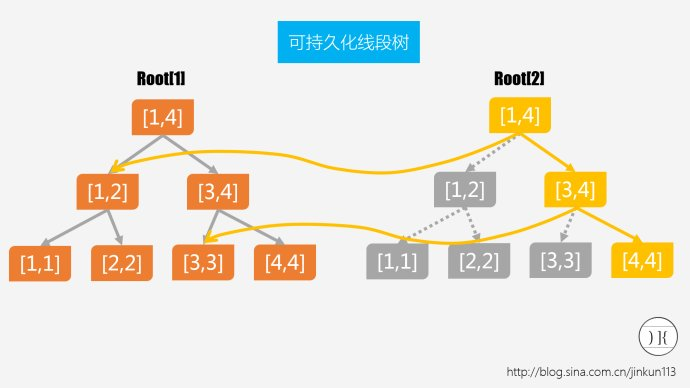
解释

我们分析一下，发现每次修改操作修改的点的个数是一样的。
（例如下图，修改了 \([1,8]\) 中对应权值为 1 的结点，红色的点即为更改的点）

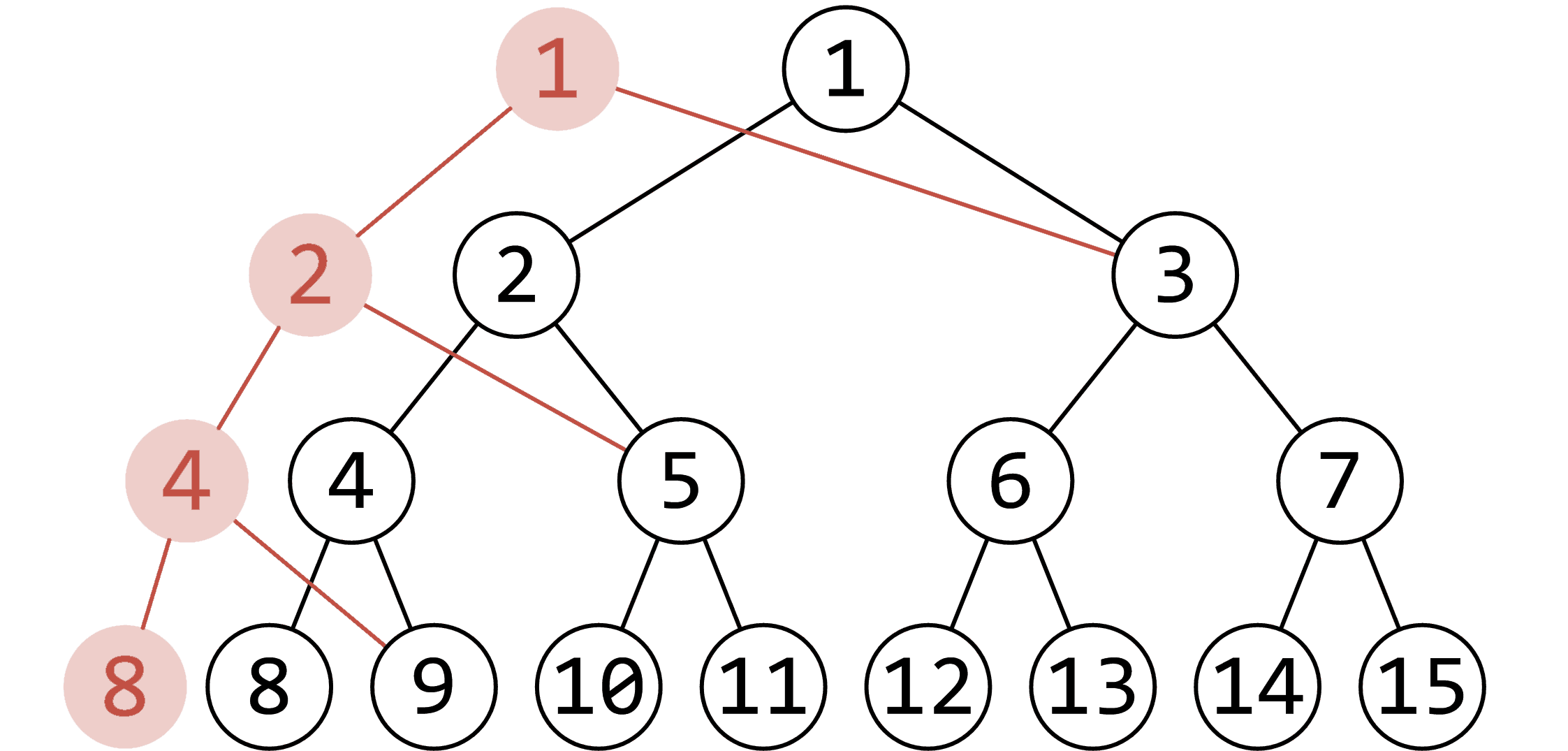
只更改了 \(O(\log{n})\) 个结点，形成一条链，也就是说每次更改的结点数 = 树的高度。
注意主席树不能使用堆式存储法，就是说不能用 \(x\times 2\)，\(x\times 2+1\) 来表示左右儿子，而是应该动态开点，并保存每个节点的左右儿子编号。
所以我们只要在记录左右儿子的基础上，保存插入每个数的时候的根节点就可以实现持久化了。

我们把问题简化一下：每次求 \([1,r]\) 区间内的 \(k\) 小值。
怎么做呢？只需要找到插入 r 时的根节点版本，然后用普通权值线段树（有的叫键值线段树/值域线段树）做就行了。

这个相信大家都能理解，回到原问题——求 \([l,r]\) 区间 \(k\) 小值。
这里我们再联系另外一个知识：前缀和。
这个小东西巧妙运用了区间减法的性质，通过预处理从而达到 \(O(1)\) 回答每个询问。

我们可以发现，主席树统计的信息也满足这个性质。
所以……如果需要得到 \([l,r]\) 的统计信息，只需要用 \([1,r]\) 的信息减去 \([1,l - 1]\) 的信息就行了。

至此，该问题解决！

关于空间问题，我们分析一下：由于我们是动态开点的，所以一棵线段树只会出现 \(2n-1\) 个结点。
然后，有 \(n\) 次修改，每次至多增加 \(\lceil\log_2{n}\rceil+1\) 个结点。因此，最坏情况下 \(n\) 次修改后的结点总数会达到 \(2n-1+n(\lceil\log_2{n}\rceil+1)\)。
此题的 \(n \leq 10^5\)，单次修改至多增加 \(\lceil\log_2{10^5}\rceil+1 = 18\) 个结点，故 \(n\) 次修改后的结点总数为 \(2\times 10^5-1+18\times 10^5\)，忽略掉 \(-1\)，大概就是 \(20\times 10^5\)。

最后给一个忠告：千万不要吝啬空间（大多数题目中空间限制都较为宽松，因此一般不用担心空间超限的问题）！大胆一点，直接上个 \(2^5\times 10^5\)，接近原空间的两倍（即 n << 5）。

实现

#include<bits/stdc++.h>
#define int long long
#define endl "\n"
using namespace std;

const int N=2e5+3;
using i64 = long long;

int n,m,q;
struct node
{
	int val,ls,rs,sum;
}tr[2*N+N*18];
int a[N];
vector<int> vy;
int rt[N],tot;
int getid(int x)  // 离散化
{
	return lower_bound(vy.begin(),vy.end(),x)-vy.begin()+1;
}
int build(int l,int r)  //建树，最初只有2*n-1个节点
{
	int p=++tot;
	if(l==r) return p;
	int mid=(l+r)/2;
	tr[p].ls = build(l,mid);
	tr[p].rs = build(mid+1,r);
	return p;
}
// pos为要插入的位置，[l,r]为操作的范围，f为该节点的历史节点
int update(int pos,int l,int r,int f)  
{
	int p=++tot;
	tr[p].ls=tr[f].ls,tr[p].rs=tr[f].rs,tr[p].sum=tr[f].sum+1;
	if(l==r) return p;
	int mid=(l+r)/2;
	if(pos<=mid) tr[p].ls=update(pos,l,mid,tr[p].ls);
	else tr[p].rs=update(pos,mid+1,r,tr[p].rs);
	return p;
}
//查询区间[l,r]的第k小数，u为前一次版本的根节点，v为当前版本的根节点
int query(int u,int v,int l,int r,int k)  
{
	int mid=(l+r)/2;
	int x=tr[tr[v].ls].sum-tr[tr[u].ls].sum; //左子树的新增个数
	if(l==r) return l;
	if(k<=x) return query(tr[u].ls,tr[v].ls,l,mid,k);  //说明左子树新增个数大于k，一定在左子树
	else return query(tr[u].rs,tr[v].rs,mid+1,r,k-x);
}
signed main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		vy.push_back(a[i]);
	}
	sort(vy.begin(),vy.end());
	vy.erase(unique(vy.begin(),vy.end()),vy.end());
	int len=vy.size();
	rt[0]=build(1,len);
	for(int i=1;i<=n;i++)
	{
		int id=getid(a[i]);
		rt[i]=update(id,1,len,rt[i-1]);  //记录每个历史版本的根节点
	}
	for(int i=1;i<=m;i++)
	{
		int l,r,k;
		cin>>l>>r>>k;
		int id=query(rt[l-1],rt[r],1,len,k); //前缀和思想
		//cout<<id<<endl;
		cout<<vy[id-1]<<endl;
	}
}

参考

主席树详解——让你躺着学会主席树

可持久化线段树