CamoTeacher:玩转半监督伪装物体检测,双一致性动态调整样本权重 | ECCV 2024
论文提出了第一个端到端的半监督伪装目标检测模型
CamoTeacher。为了解决半监督伪装目标检测中伪标签中存在的大量噪声问题,包括局部噪声和全局噪声,引入了一种名为双旋转一致性学习(DRCL)的新方法,包括像素级一致性学习(PCL)和实例级一致性学习(ICL)。DRCL帮助模型缓解噪音问题,有效利用伪标签信息,使模型在避免确认偏差的同时可以获得充分监督。广泛的实验验证了CamoTeacher的优越性能,同时显著降低了标注要求。来源:晓飞的算法工程笔记 公众号
论文: CamoTeacher: Dual-Rotation Consistency Learning for Semi-Supervised Camouflaged Object Detection

Introduction
伪装物体检测(COD)旨在识别在其环境中完全融入的物体,包括动物或具有保护色彩并具有融入周围环境能力的人造实体,这一任务由于低对比度、相似纹理和模糊边界而变得复杂。与一般物体检测不同,COD受到这些因素的挑战,使得检测变得格外困难。现有的COD方法严重依赖于大规模的像素级注释数据集,其创建需要大量的人力和成本,从而限制了COD的进展。
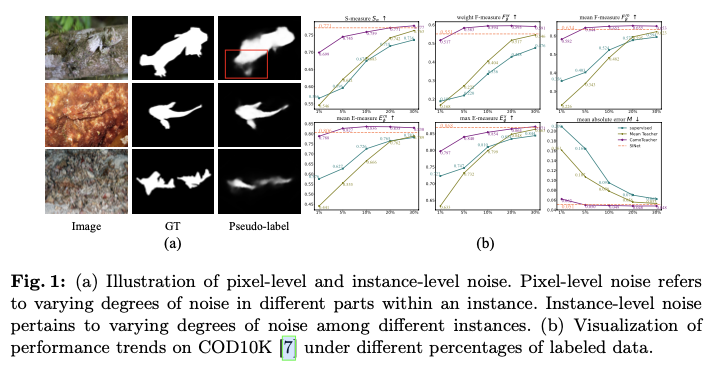
为了缓解这一问题,半监督学习作为一种有希望的方法出现,利用标记和未标记数据。然而,由于复杂的背景和微妙的物体边界,其在COD中的应用并不直接。半监督学习在COD中的有效性受到伪标签中存在的大量噪声的严重影响,伪标签的噪声有两种主要类型:像素级噪声,表明在单个伪标签内的变化,以及实例级噪声,显示不同伪标签之间的变化。这种区分是至关重要的,因为它指导了如何改进伪标签质量以提高模型训练的方法。(1)像素级噪声的特点是在伪标签的各个部分内部的标注不一致。如图1a中所示,在第一行中,壁虎的尾部在视觉上比头部更难以识别。由SINet生成的伪标签在其尾部区域中的准确性较低(由红色框标出)。这一观察结果强调了对伪标签内的所有部分统一处理的不当性。(2)实例级噪声指的是不同伪标签之间噪声水平的变化。如图1a所示,第三行的伪标签与第二行相比不太准确,因为第三行中的伪装对象更难以检测。这些差异表明每个伪标签对模型训练的贡献是不同的,强调了需要对整合伪标签信息采取细致差异的方法。
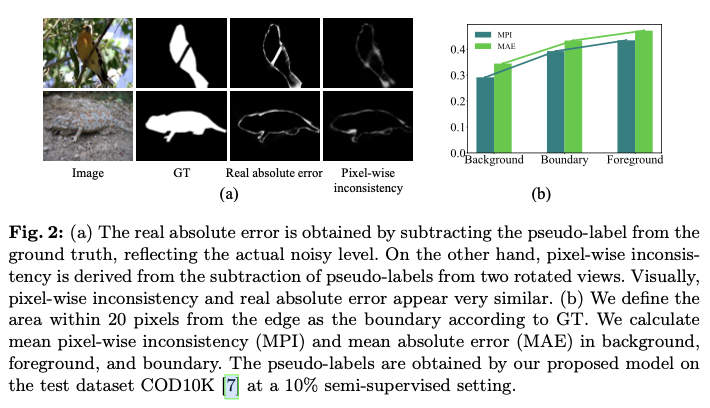
为了解决在没有未标记GT的数据的情况下评估伪标签噪声的挑战,论文提出了基于两个旋转视图的像素级不一致性和实例级一致性的两种新策略。具体来说,对于像素级噪声,论文观察到通过比较两个旋转视图的伪标签计算出的像素级不一致性,可以反映相对于GT的实际误差,如图2a所示。这种关系显示了不同部分之间平均像素级不一致性与平均绝对误差(MAE)之间的正相关性,如图2b的折线所示。因此,具有较高像素级不一致性的区域更容易出现不准确性,表明在训练过程中需要减弱这些区域的重要性。
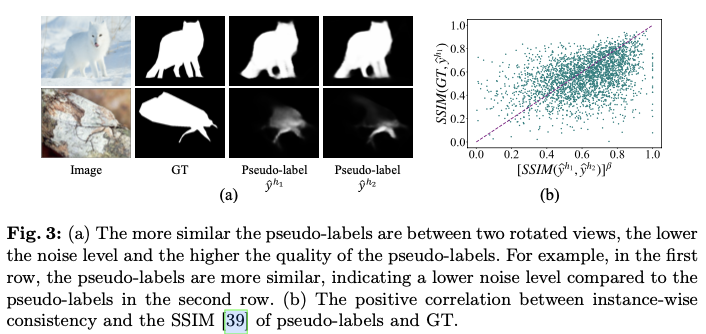
对于实例级噪声,跨旋转视图具有更大相似性的伪标签展示了更低的噪声水平,如图3a所示。伪标签和GT计算的SSIM之间的实例级一致性与正相关性进一步支持了这一观察结果,如图3b所示。因此,表现出更高实例级一致性的伪标签可能具有更高质量,并应在学习过程中优先考虑。
通过这些观察结果,论文提出了一种名为CamoTeacher的半监督伪装物体检测框架,该框架结合了一种名为Dual-Rotation Consistency Learning(DRCL)的新方法。具体而言,DRCL通过两个核心组件来实现其策略:像素级一致性学习(PCL)和实例级一致性学习(ICL)。PCL通过考虑不同旋转视图之间的像素级不一致性,创新地为伪标签中的不同部分分配可变权重。同时,ICL根据实例级一致性调整各个伪标签的重要性,实现细致、噪声感知的训练过程。
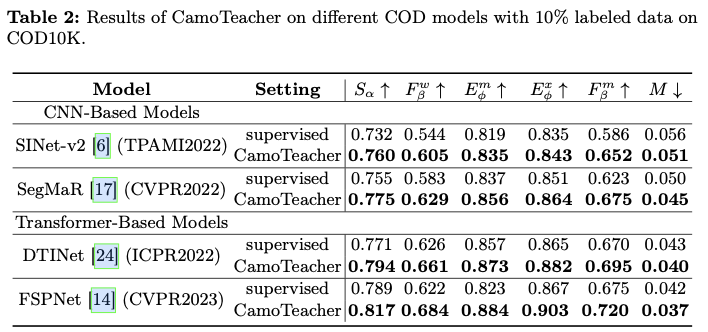
论文采用SINet作为基础模型来实现CamoTeacher,并将其应用于更经典的伪装物体检测(COD)模型,即基于CNN的SINet-v2和SegMaR,以及基于Transforme的DTINet和FSPNet。在四个COD基准数据集(即CAMO,CHAMELEON,COD10K和NC4K)上进行了大量实验,结果显示CamoTeacher不仅在与半监督学习方法相比方面达到了最先进的水平,而且与已建立的全监督学习方法相媲美。具体来说,如图1b所示,仅使用了20%的标记数据,它几乎达到了在COD10K上全监督模型的性能水平。
论文的贡献可以总结如下:
-
引入了第一个端到端的半监督伪装物体检测框架
CamoTeacher,为未来半监督伪装物体检测的研究提供了一个简单而有效的基准。 -
为解决半监督伪装物体检测中伪标签中大量噪声的问题,提出了
Dual-Rotation Consistency Learning(DRCL),其中包括Pixel-wise Consistency Learning(PCL)和Instance-wise Consistency Learning(ICL),允许自适应调整不同质量伪标签的贡献,从而有效利用伪标签信息。 -
在
COD基准数据集上进行了大量实验,相较于完全监督设置,取得了显著的改进。
Methodology
Task Formulation
半监督伪装物体检测旨在利用有限的标记数据训练一个能够识别与周围环境无缝融合的物体的检测器。由于物体与背景之间的对比度较低,这个任务本身具有挑战性。给定一个用于训练的伪装物体检测数据集 \(D\) ,含 \(M\) 个标记样本的标记子集表示为 \(D_L=\{x_i^{l}, y_i\}_{i=1}^{M}\) ,含 \(N\) 个未标记样本的未标记子集表示为 \(D_U=\{x_i^{u}\}_{i=1}^{N}\) ,其中 \(x_i^{l}\) 和 \(x_i^{u}\) 表示输入图像, \(y_i\) 表示标记数据的相应注释掩码。通常, \(D_L\) 只占整个数据集 \(D\) 的很小一部分,这突出了 \(M \ll N\) 的半监督学习场景。对于 \(M \ll N\) 的强调,强调了半监督学习中的挑战和机遇:通过利用未标记数据 \(D_U\) 尚未发掘的潜力来提升检测能力,而这远远超过了标记子集 \(D_L\) 。
Overall Framework
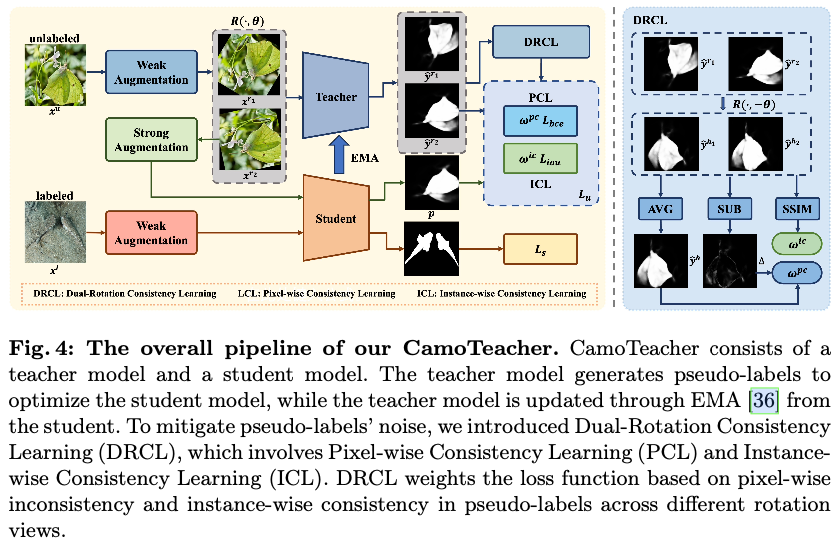
如图4所示,采用Mean Teacher作为初步方案,以实现端到端的半监督伪装物体检测框架。该框架包含两个具有相同结构的COD模型,即教师模型和学生模型,分别由参数 \(\Theta_t\) 和 \(\Theta_s\) 参数化。教师模型生成伪标签,然后用于优化学生模型。整体损失函数 \(L\) 可以定义为:
其中, \(L_s\) 和 \(L_u\) 分别表示有监督损失和无监督损失, \(\lambda_u\) 是平衡损失项的无监督损失权重。按照经典的COD方法,使用二元交叉熵损失 \(L_{bce}\) 用于训练。
在训练过程中,采用弱数据增强 \(\mathcal{A}^w(\cdot)\) 和强数据增强 \(\mathcal{A}^s(\cdot)\) 策略的组合。弱数据增强应用于有标记数据以减轻过拟合,而无标记数据在强数据增强下经历各种数据扰动,以创造同一图像的不同视角。有监督损失 \(L_s\) 的定义如下:
其中, \(F(\mathcal{A}(x_i);\Theta)\) 表示模型 \(\Theta\) 对第 \(i\) 张图像在增强 \(\mathcal{A}(\cdot)\) 下的检测结果。对于无标记的图像,首先应用弱数据增强 \(\mathcal{A}^w(\cdot)\) ,然后将其传递给教师模型。这一初始步骤对于在不显著改变图像核心特征的变化下生成可靠的伪标签 \(\widehat{y_i}\) 至关重要。这些伪标签作为学生模型的一种软监督形式。接下来,相同的图像经过强数据增强 \(\mathcal{A}^s(\cdot)\) 后传递给学生模型。这个过程引入了更高层次的变异性和复杂性,模拟更具挑战性的条件,以适应学生模型。学生模型基于这些经过强增强的图像生成预测 \(p_i\) ,利用伪标签 \(\widehat{y_i}\) 作为无标记数据学习的指导。可以将其形式化为:
因此,无监督损失 \(L_u\) 可以表示为:
最后,学生模型通过总损失 \(L\) 进行密集训练,该损失包含了半监督框架中有监督和无监督学习的两个方面。这种方法确保学生模型从有标记和伪标记数据中受益,提高其检测能力。同时,教师模型通过指数移动平均(EMA)机制进行系统更新,有效地提取学生知识并防止噪音干扰,具体表述为:
其中, \(\eta\) 是一个超参数,表示保留的比例。
Dual-Rotation Consistency Learning
由于物体的伪装性质,伪标签中包含大量噪音,直接使用它们来优化学生模型可能会损害模型的性能。为解决这个问题,最直观的一个可能方法是设置一个固定的高阈值来过滤高质量的伪标签,但这会导致召回率较低,并使得难以充分利用伪标签的监督信息。为此,论文提出了双旋转一致性学习(DRCL),以动态调整伪标签的权重,减少噪音的影响。
对图像 \(x_i\) 进行两个独立的随机旋转,其中 \(x_i\) 在之前已进行了翻转和随机调整大小,得到两个不同的旋转视图 \(x_i^{r_1}\) 和 \(x_i^{r_2}\) 。
其中, \(x_i^{r} = R(x_i, \theta)\) 表示将输入图像 \(x_i\) 旋转 \(\theta\) 度。将获得的旋转视图输入到教师模型中,得到相应的预测值,即 \(\widehat y_i^{r} = F(x_i^{r}; \Theta_t)\) 。随后,对预测值进行 \(-\theta\) 的相反旋转,使其返回到原始的水平方向,得到 \(\widehat y_i^{h_1}\) 和 \(\widehat y_i^{h_2}\) ,以便在不同的旋转视图下计算预测不一致性。
请注意,旋转会引入黑色的边界区域,这些区域不参与DRCL的计算过程。
由于伪标签的不同区域和不同伪标签之间的噪声水平不同,引入PCL和ICL动态调整不同像素在伪标签内部和各个伪标签之间的贡献。
-
Pixel-wise Consistency Learning
在像素级别上对水平预测 \(\widehat y_i^{h_1}\) 和 \(\widehat y_i^{h_2}\) 进行减法运算,得到像素级别的不一致性 \(\Delta_i\) 。
不同视图之间的像素级不一致性 \(\Delta_i\) 反映了伪标签的可靠性。然而,在两个旋转视图的预测值都接近0.5的情况下, \(\Delta_i\) 无法有效区分它们。这些预测表现出高度的不确定性,意味着不能明确将它们分类为前景或背景,并且很可能代表嘈杂的标签。因此,有必要通过降低它们的权重来减弱它们的影响。因此,计算水平预测值 \(\widehat y_i^{h}\) 的平均值,
其中, \(avg(\cdot, \cdot)\) 表示计算两个像素级别输入的平均值,并使用其与0.5的L2距离作为调整权重的一个组成部分。
因此,根据不同旋转视图之间的像素级别不一致性,推导出像素级别一致性权重 \(\omega_i^{pc}\) ,如下所示:
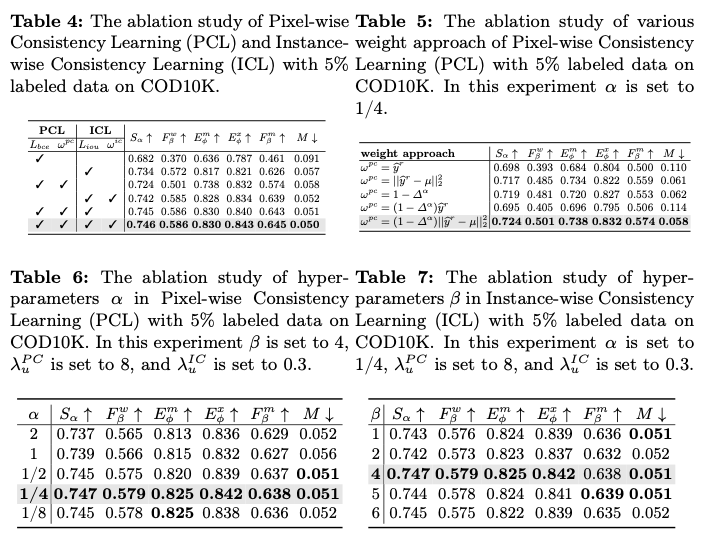
其中, \(\alpha\) 是一个超参数, \(\mu=0.5\) 。这个动态的像素级一致性权重 \(\omega_i^{pc}\) 会给与不同旋转视图间预测一致的区域分配更高的权重,而对于预测不一致的区域则分配较小的权重。
总而言之,将PCL损失函数 \(L_u^{PC}\) 表述为:
自适应地调整每个像素的权重,以确保对学生模型进行全面监督,同时避免带来偏见。
-
Instance-wise Consistency Learning
不同图像之间的伪装程度会有所不同,导致伪标签质量在图像之间存在显著变化。平等地对待所有伪标签是不合理的。不幸的是,对于未标记的图像,评估伪标签质量是具有挑战性的,因为没有可用的GT标签。论文呢观察到两个旋转视图的实例一致性和伪标签质量之间存在正相关,由SSIM量化。基于此,引入ICL来调整具有不同质量的伪标签的贡献。将实例级一致性权重 \(\omega_i^{ic}\) 表示如下:
其中, \(\beta\) 是一个超参数,用于调整实例级一致性和伪标签质量之间的分布关系。
使用交并比(IoU)损失作为实例级限制,因此,ICL损失可以表示为:
因此,最终的总损失 \(L\) 由三个部分组成:有监督损失 \(L_s\) ,PCL损失 \(L_u^{LC}\) 和ICL损失 \(L_u^{GC}\) ,可以表示为:
其中, \(\lambda_u^{pc}\) , \(\lambda_{u}^{ic}\) 是超参数。
Experiment
Experiment Settings
-
Dataset
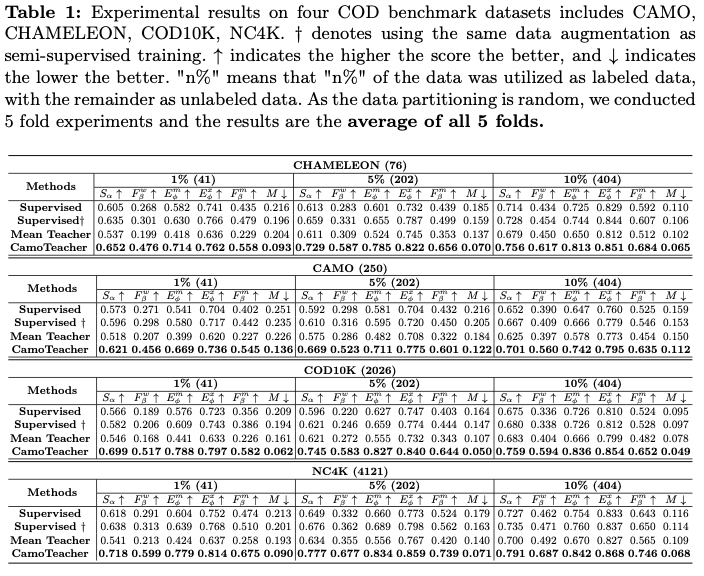
在四个基准数据集CAMO、CHAMELEON、COD10K和NC4K上评估了CamoTeacher模型。在CAMO数据集中,共有2500张图像,包括1250张伪装图像和1250张非伪装图像。CHAMELEON数据集包含76张手动注释图像。COD10K数据集由5066张伪装图像、3000张背景图像和1934张非伪装图像组成。NC4K是另一个包含4121张图像的大规模COD测试数据集。根据先前的工作中的数据划分,使用COD10K的3040张图像和CAMO的1000张图像作为实验的训练集。剩余的图像来自这两个数据集,被用作测试集。在训练过程中,采用了半监督分割的数据划分方法。我们从训练集中随机采样了1%、5%、10%、20%和30%的图像作为有标签的数据,剩余的部分作为无标签的数据。
-
Evaluation Metrics
参考先前的工作,在COD中使用了6个常见的评估指标来评估我们的CamoTeacher模型,包括S-measure( \(S_{\alpha}\) )、加权F-measure( \(F_{\beta}^w\) )、平均E-measure( \(E_{\phi}^m\) )、最大E-measure( \(E_{\phi}^x\) )、平均F-measure( \(F_{\beta}^m\) )和平均绝对误差( \(M\) )。
-
Implementation Details
提出的CamoTeacher模型使用PyTorch进行实现。采用SINet作为COD模型的基线。使用带有动量0.9的SGD优化器和多项式学习率衰减,初始学习率为0.01,来训练学生模型。训练周期设置为40个周期,其中前10个周期为burn-in阶段。批量大小为20,有标签数据和无标签数据的比例为1:1,即每个批次包含10个有标签和10个无标签的图像。在训练和推断过程中,每个图像被调整为 \(352 \times 352\) 的大小。通过EMA方法更新教师模型,动量 \(\eta\) 为0.996。弱数据增强包括随机翻转和随机缩放,而强数据增强涉及颜色空间转换,包括Identity、Autocontrast、Equalize、Gaussian blur、Contrast、Sharpness、Color、Brightness、Hue、Posterize、Solarize,从这个列表中随机选择最多3个。
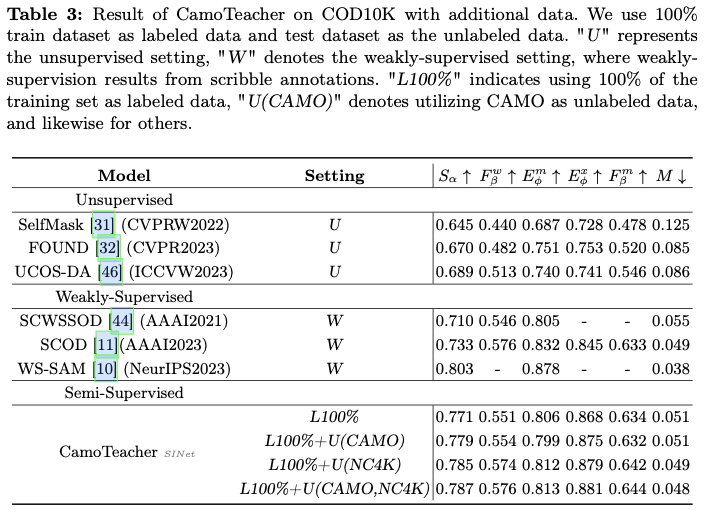
Results

如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】





 浙公网安备 33010602011771号
浙公网安备 33010602011771号