浅谈线段树
线段树
在一类问题中,我们需要经常处理可以映射在一个坐标轴上的一些固定线段,例如说映射在OX轴上的线段。由于线段是可以互相覆盖的,有时需要动态地取线段的并,例如取得并区间的总长度,或者并区间的个数等等。一个线段是对应于一个区间的,因此线段树也可以叫做区间树。
线段树的构造思想
线段树是一棵二叉树,树中的每一个结点表示了一个区间[a,b]。每一个叶子节点表示了一个单位区间。对于每一个非叶结点所表示的结点[a,b],其左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2,b]。
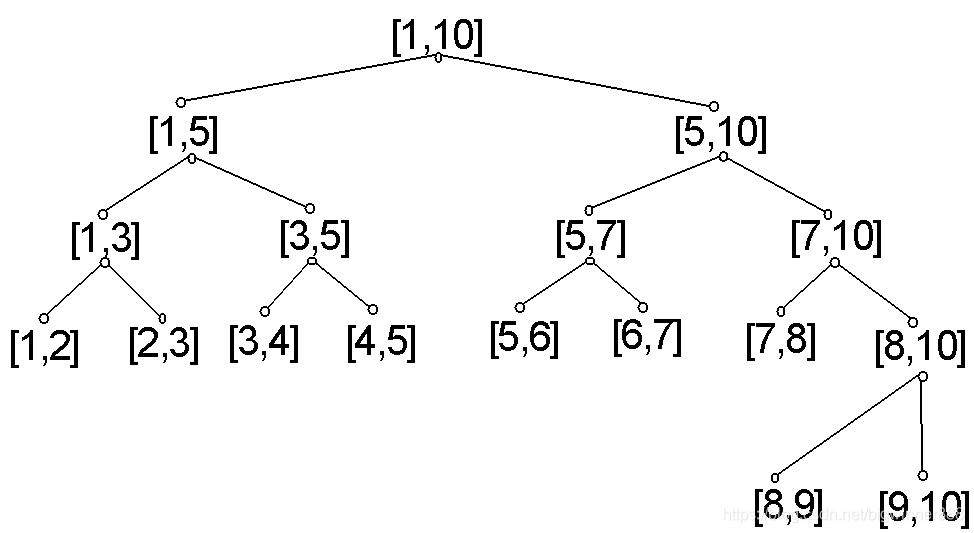
线段树的运用
线段树的每个节点上往往都增加了一些其他的域。在这些域中保存了某种动态维护的信息,视不同情况而定。这些域使得线段树具有极大的灵活性,可以适应不同的需求。
练习一:
题目描述:
桌子上零散地放着若干个盒子,桌子的后方是一堵墙。如右图所示。现在从桌子的前方射来一束平行光, 把盒子的影子投射到了墙上。问影子的总宽度是多少?
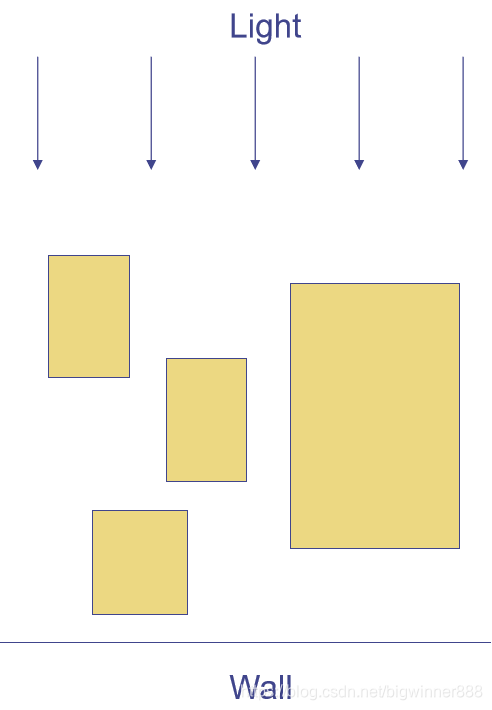
样例输入:
20 //桌面总宽度
4 //盒子数量
1 5
3 8
7 10
13 19
样例输出:
15
分析
抽象化题目:x轴上有若干条线段,求线段覆盖的总长度。
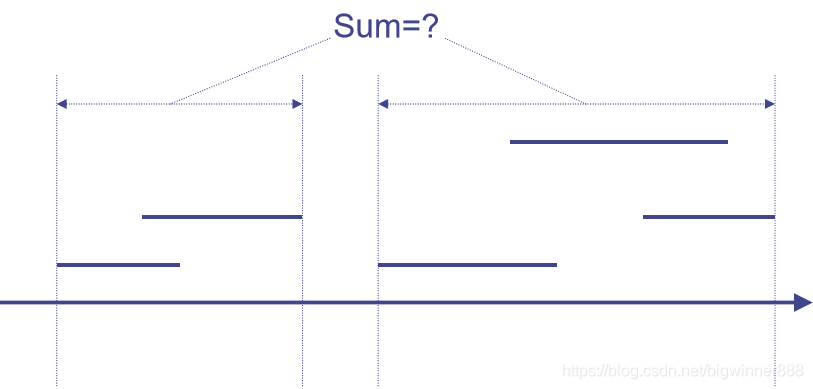
对于线段树,我们将每一个节点增加一个域,
0表示这一区间没有被完全覆盖,1表示这一区间被完全覆盖。
那我们将这个域设置好后,统计总共覆盖的长度其实就简单了,
以二叉树的遍历方式,判断每一个节点的域是否为一,如果为1我们就统计一下长度,就欧了。
如果当前节点为一,就不能再往下遍历,因为它的子节点是包括在当前节点里面的
插入算法(设置域)
void insert(int x, int l, int r, int a, int b)
{
int mid=(l + r) >> 1;
if(tree[x]) return ; //如果已设置了
if((l == a) && (r == b)) tree[x]=1; //完全被覆盖
else if(b <= mid) insert(2 * x, l, mid, a, b); //区间在左边
else if(a >= mid) insert(2 * x + 1, mid, r, a, b); //区间在右边
else //区间在左右两边都有覆盖。例:左(3,4) 右(4,6) 插入(3,5)
insert(2 * x, l, mid, a, mid), //二分
insert(2 * x + 1, mid, r, mid, b);
}
统计算法
void ccount(int x, int l, int r)
{
int mid=(l + r) >> 1;
if(tree[x]) ans+=(r - l);
else if(l+1<r) //当前节点还包括多个点,想(3,4)就不能搜下去了
ccount(2 * x, l, mid),
ccount(2 *x + 1, mid, r);
}
注意:count在c++中是关键字,所以不能将其命名为函数名
code:
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<queue>
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
#define ll long long
using namespace std;
const int MAX=2147483647;
const int N=3e5+10;
int n, num, l, r, tree[N], ans;
void insert(int x, int l, int r, int a, int b)
{
int mid=(l + r) >> 1;
if(tree[x]) return ;
if((l == a) && (r == b)) tree[x]=1;
else if(b <= mid) insert(2 * x, l, mid, a, b);
else if(a >= mid) insert(2 * x + 1, mid, r, a, b);
else
insert(2 * x, l, mid, a, mid),
insert(2 * x + 1, mid, r, mid, b);
}
void ccount(int x, int l, int r)
{
int mid=(l + r) >> 1;
if(tree[x]) ans+=(r - l);
else if(l+1<r)
ccount(2 * x, l, mid),
ccount(2 *x + 1, mid, r);
}
int main()
{
//fre();
scanf("%d%d", &n, &num);
for(int i=1; i<=num; i++)
{
scanf("%d%d", &l, &r);
insert(1, 1, n, l, r);
}
ccount(1, 1, n);
printf("%d", ans);
return 0;
}
练习二:
题目描述:
桌子上零散地放着若干个不同颜色的盒子,桌子的后方是一堵墙。如右图所示。问从桌子前方可以看到多少个盒子?假设人站得足够远(自己设计测试数据,输入时,由底向上,从左到右)。
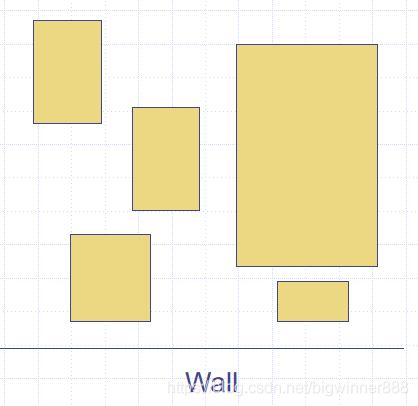
样例输入:
16 //桌子长度
5 // 盒子数量
4 7
12 14
1 5
6 10
11 16
样例输出:
4
分析:
可以这样来看这道题:x轴上有若干条不同线段,将它们依次染上不同的颜色,问最后能看到多少种不同的颜色?(后染的颜色会覆盖原先的颜色)
我们定义一开始x轴的颜色初始为0,第一条线段的颜色为1,第二条线段的颜色为2,第三条线段的颜色为3,以此类推。
原先构造线段树的方法不再适用,但是我们可以通过修改线段树的cover域的定义,使得这道题也能用线段树来解。
定义cover如下:cover=-1表示该区间由多种颜色组成。cover>0表示该区间只有一种单一的颜色cover(不包括初始颜色)。
使用一个数组F,初始化为0。遍历线段树,对于每种颜色c对F[c]赋值1。最后统计F中1的个数即可。(注意颜色0应该排除在外)
插入算法:
void insert(int x, int l, int r, int a, int b, int color)
{
int mid=(l + r) >> 1;
if(tree[x] == color) return ; //如果已设置了
if((l == a) && (r == b)) {tree[x]=color; return ;} //完全覆盖
if(tree[x] > 0) //有多个颜色
{
tree[2 * x]=tree[2 * x + 1]=tree[x];
tree[x]=-1; //多种颜色为-1
}
if(b <= mid) insert(2 * x, l, mid, a, b, color); //区间在左边
else if(a >= mid) insert(2 * x + 1, mid, r, a, b, color);//区间在右边
else ////区间在左右两边
{
insert(2 * x, l, mid, a, mid, color), //二分
insert(2 * x + 1, mid, r, mid, b, color);
}
}
统计算法:
void ccount(int x, int l, int r)
{
int mid=(l + r) >> 1;
if(tree[x] > 0)
{
f[tree[x]]=1;
printf("%d %d\n", l, r);
}
else if((l + 1) < r)
ccount(2 * x, l, mid),
ccount(2 * x + 1, mid, r);
}
code:
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<queue>
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
#define ll long long
using namespace std;
const int MAX=2147483647;
const int N=3e5+10;
int n, num, l, r, tree[N], ans, f[N];
void insert(int x, int l, int r, int a, int b, int color)
{
int mid=(l + r) >> 1;
if(tree[x] == color) return ;
if((l == a) && (r == b)) {tree[x]=color; return ;}
if(tree[x] > 0)
{
tree[2 * x]=tree[2 * x + 1]=tree[x];
tree[x]=-1;
}
if(b <= mid) insert(2 * x, l, mid, a, b, color);
else if(a >= mid) insert(2 * x + 1, mid, r, a, b, color);
else
{
insert(2 * x, l, mid, a, mid, color),
insert(2 * x + 1, mid, r, mid, b, color);
}
}
void ccount(int x, int l, int r)
{
int mid=(l + r) >> 1;
if(tree[x] > 0)
{
f[tree[x]]=1;
printf("%d %d\n", l, r);
}
else if((l + 1) < r)
ccount(2 * x, l, mid),
ccount(2 * x + 1, mid, r);
}
int main()
{
//fre();
scanf("%d%d", &n, &num);
for(int i=1; i<=num; i++)
{
scanf("%d%d", &l, &r);
insert(1,1,n,l,r,i);
}
ccount(1, 1, n);
for(int i=1; i<=num; i++) if(f[i]) ans++;
printf("%d", ans);
return 0;
}
练习三:
题目描述:
给定一条长度为m的线段,有n个操作,每个操作有3个数字x,y,z表示把区间[x,y]染成颜色z,询问染完色之后,这条长度为m的线段一共有几种颜色。规定:线段的颜色可以相同。连续的相同颜色被视作一段。问x轴被分成多少段。

样例输入
4 20 //四条,总长度为2020
10 19 1
2 9 2
5 13 3
15 17 4
样例输出
7
分析:
其实这题只是练习二稍作改动的扩展。
至于插入算法,我们还是同上(注意:这里必须包括0这一种颜色)
那统计算法怎么去做呢?
其实我们只要判断当前这一个区间是一个单独的color&&
当前的颜色与上一个区间的颜色不同,
那是不是又被分成了一个新段(ans++)。
插入算法:
void insert(int x, int l, int r, int a, int b, int color)
{
if((l == a) && (r == b)) {tree[x]=color; return ;} //更新颜色
if(tree[x] >= 0) //多种颜色(包括0哦,0也是也是可能被分成一个新段的)
{
tree[2 * x]=tree[2 * x + 1]=tree[x];
tree[x]=-1; //往下传递
}
int mid=(l + r) >> 1;
if(b <= mid) insert(2 * x, l, mid, a, b, color);
else if(a >= mid) insert(2 * x + 1, mid, r, a, b, color);
else
{
insert(2 * x, l, mid, a, mid, color);
insert(2 * x + 1, mid, r, mid, b, color);
}
}
统计算法:
int ccount(int x, int l, int r)
{
int mid=(l + r) >> 1;
if(tree[x] >= 0)
{
int s=1; //默认不同
if(temp == tree[x]) s=0;
//如果与上一段的颜色相同,那是不是就是同一段,不贡献答案
temp=tree[x]; //更新
return s;
}
return ccount(2 * x, l, mid)+ccount(2 * x + 1, mid, r);
}
练习四:
题目描述:
在平面内有一条长度为n的线段(不计入答案),可以对进行以下2种操作:
- 把从x到y的再加一条线段
- 查询从x到x+1有多少条线段
样例输入
7 2
2 5
3 6
4 5
样例输出
2
提前声明,前面的三道例题中的code(用了类似动态开点的方法),并没有那么的专业,于是在后面的两题中,我会规范模板,勿喷!!!
分析:
为线段树每个节点增加一个Count域。表示所对应区间上重叠的线段数。
思考线段树的构造方法:当某线段能够完整覆盖某个结点所对应的区间时,则不再二分。因此要统计某个单位区间上重叠的线段总数,必须把从叶结点到根结点路径上所有结点的count域累加。
建树算法:
void build(int x, int l, int r)
{
if((tree[x].l + 1) < tree[x].r)
{
int mid=(tree[x].l + tree[x].r) >> 1;
tree[2 * x].l=tree[x].l, tree[2 * x].r=mid;
tree[2 * x + 1].l=mid, tree[2 * x + 1].r=tree[x].r;
build(2 * x, l, mid), build(2 * x + 1, mid, r);
}
}
插入算法:
void insert(int x, int l, int r)
{
int mid=(tree[x].l + tree[x].r) >> 1;
if((tree[x].l == l) && (tree[x].r == r)) {tree[x].val++;return ;}
if(r <= mid) insert(2 * x, l, r);
else if(l >= mid) insert(2 * x + 1, l, r);
else
insert(2 * x, l, mid),insert(2 * x + 1, mid, r);
}
统计算法:
int ccount(int x, int l, int r)
{
int ans=tree[x].val;
while((tree[x].l + 1) < tree[x].r)
{
int mid=(tree[x].l + tree[x].r) >> 1;
if((tree[x].l == l) && (tree[x].r == r)) break;
else if(r <= mid) ans+=tree[2 * x].val, x*=2;
else if(l >= mid) ans+=tree[2 * x + 1].val, x=x * 2 + 1;
//累加路径上的覆盖值
}
return ans;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号