数论基础
质数
质数这东西让我联想到了原子,一样不可拆分,所以我们说质数具有原子性。
我们设\(\pi(x)\)为不大于x的质数个数,可得\(\pi(x)=O(\frac x{\ln(x)})\)
唯一分解定理
任何一个\(N(N>1)\)能被质数分解,且只有一种分解方式,即
\(N=p_1^{c_1}\times p_2^{c_2}\times……\times p_m^{c_m}(N>1)\)
其中\(p_i\) 为素数,\(c_i\) 为正整数,
满足\(p_1<p_2<……<p_m\)
筛质数
可得:对于\(n\),最多只有一个质因子大于\(\sqrt n\) 。
证明:若两个质因子\(a>\sqrt n,b>\sqrt n\)
\(~~~~~~~~~~\) 则\(a\times b>n\)(不成立),即原命题正确。
暴力试除法
根据上述结论我们对于一个数,只需要枚举1~\(\sqrt n\) 即可,
这里就不给代码了,时间复杂度O(\(n\sqrt n\))
埃式筛法
枚举到一个质数,我们只需要将它的倍数全部标记即可,没被标记的就是质数,这里给出核心代码。
int prime[100005],flag[100005],tot;
void find(int n)
{
for(int i=2;i<=n;i++)
if(!flag[i])
{
flag[i]=1;
prime[++tot]=i;
for(int j=2;j<=n/i;j++)
flag[i*j]=1;
}
for(int i=1;i<=tot;i++)
printf("%d ",prime[i]);
}
欧拉筛法(线性筛法)
埃式筛法已经接近\(O(n)\)的复杂度了,但是优化的余地。
对于一个数,可能被多次标记,我们可以减少它们的次数,来达到优化的目的。
例如:30,它可以被分解成:
\(30=2\times15=3\times10=5\times6\)
根据上述的唯一分解定理,我们只需要用最小的质因子来分解。
例如:30分解成\(30=2\times15\)。
int prime[100005],flag[100005],tot;
void find(int n)
{
for(int i=2;i<=n;i++)
{
if(!flag[i]) prime[++tot]=i;
for(int j=1;j<=tot&&prime[j]*i<=n;j++)
{
flag[i*prime[j]]=1;
if(i%prime[j]==0) break;
}
}
for(int i=1;i<=tot;i++)
printf("%d ",prime[i]);
}
整除
令\(a∣b\)表示\(a\)整除\(b\),其中\(b\)是\(a\)的倍数,\(a\)是\(b\)的约数。
一些性质:
1、若\(d∣a\),有\(d∣ka\)。
2、对称性:若\(a∣b,b∣a\),有\(a = b\)。
3、传递性:若\(c∣b,b∣a\),则\(c∣a\)。
4、若\(c∣a,d∣b\),则\(cd∣ab\)。
5、若\(c∣a,c∣b\),则\(c∣(ma+nb)\)
约数:
若\(N=p_1^{c_1}\times p_2^{c_2}\times……\times p_m^{c_m}(N>1)\)
其中\(p_i\)为素数,\(c_i\)为正整数,
满足\(p_1<p_2<……<p_m\) ,
则N 的正约数集合\(\{p_1^{b_1},p_2^{b_2},……,p_m^{b_m}\}\),
其中\(0\le b_i\le c_i\)
由此可推出如下两条公式:
- N的约数个数:\(\prod^m_{i=1}c_i+1\)
- N的约数的和:\(\prod_{i=1}^m(\sum^{c_j}_{j=0}(p_i)^j)\)
最大公约数和最小公倍数
我们设\(gcd(a,b)\)为\(a、b\)的最大公约数。
\(~~~~~~~~~~lcm(a,b)\)为\(a、b\)的最下公倍数。
求\(lcm(a,b)\)和\(gcd(a,b)\;\;interesting\)的方法:
将a,b分解质因数,得:
\(a=p_1^{a_1}\times p_2^{a_2}\times……\times p_m^{a_m}\)
\(b=p_1^{b_1}\times p_2^{b_2}\times……\times p_m^{b_m}\)
那么\(gcd(a,b)=p_1^{min(a_1,b_1)}\times p_2^{min(a_2,b_2)}\times……\times p_m^{min(a_m,b_m)}\)
\(~~~~~~lcm(a,b)=p_1^{max(a_1,b_1)}\times p_2^{max(a_2,b_2)}\times……\times p_m^{max(a_m,b_m)}\)
欧几里得算法
\(gcd(a,b)=gcd(b,a\bmod b)\)
我们可以根据这个求出\(gcd(a,b)\)。
更相减损法
\(gcd(a,b)=gcd(b,a-b)=gcd(a,a-b)\)
\(gcd(2a,2b)=2gcd(a,b)\)
根据上述可得\(gcd(a,b)\)。
互质
\(gcd(a,b)=1:a,b\)互质。
\(gcd(a,b,c)=1:a,b,c\)互质。
\(gcd(a,b)=gcd(b,c)=gcd(a,c)=1\):三者两两互质。
欧拉函数
欧拉函数\(\varphi(n)\),表示\(1~n\)中与\(n\)互质的个数。
若\(N=p_1^{c_1}\times p_2^{c_2}\times……\times p_m^{c_m}\) ,
其中\(p_i\)为素数,\(c_i\) 为正整数,
满足\(p_1<p_2<……<p_m\) ,
\(\varphi(n)=N\times \frac{p_1-1}{p_1} \times \frac{p_2-1}{p_2}\times……\times\frac{p_m-1}{p_m}=N\times \prod(1-\frac1p)\)
一些性质
-
\(\varphi(1)=1\)
-
p是质数,\(\varphi(p)=p-1\)。
-
p是质数,n = \(p^k\) , \(\varphi(n)=p^k-p^{k-1}=(p-1)p^{k-1}\)
-
\(gcd(a,b)=1,\varphi(ab)=\varphi(a)\times\varphi(b)\)(积性函数)。
-
对于质数p,有
\(~~~~~n\%p=0,\varphi(np)=\varphi(n)\times p\)
\(~~~~~n\%p\neq0,\varphi(np)=\varphi(n)\times(p-1)=\varphi(n)\times\varphi(p)\) -
对于n>1,\(1-n\)中与n互质的数的和为\(n\times\frac{\varphi(n)}2\)
-
\(\sum_{d|n}\varphi(d)=n\)
欧拉筛求欧拉函数
根据上述性质:
每次枚举出一个质数i,\(phi_i=i-1\)。
根据第5个性质,即可推出。
int prime[100005],flag[100005],phi[100005],tot;
void find(int n)
{
phi[1]=1;
for(int i=2;i<=n;i++)
{
if(!flag[i]) prime[++tot]=i,phi[i]=i-1;
for(int j=1;j<=tot&&prime[j]*i<=n;j++)
{
flag[i*prime[j]]=1;
if(i%prime[j]==0)
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else phi[i*prime[j]]=phi[i]*phi[prime[j]];
}
}
for(int i=1;i<=n;i++)
printf("%d ",phi[i]);
}
同余
用m除整数a,b余数相同,称a和b对模m同余,记作\(a\equiv b\pmod m\)
两个概念:
- 标准剩余系,每个同余系的任意两个整数模m同余。
- 既约剩余系,每个同余系的任意整数与m互质。
一些性质1:
- \(a\equiv b\pmod m\),当且仅当\(m|(a-b)\)。
- \(a\equiv b\pmod m\),当且仅当最在整数k,使得\(a=b+km\)
一些性质2:
有整数a,b,c,自然数m,n
- 自反性:\(a\equiv a\pmod m\)。
- 对称性:若\(a\equiv b\pmod m\),则\(b\equiv a\pmod m\)。
- 传递性:\(a\equiv b\pmod m,b\equiv c\pmod m,a\equiv c\pmod m\)
- 同加性:\(a\equiv b\pmod m,a+c\equiv b+c\pmod m\)
- 同乘性:\(a\equiv b\pmod m,ac\equiv bc\pmod m\)
- 同幂性:\(a\equiv b\pmod m,a^n\equiv b^n\pmod m\)
- 若\(a \bmod p=x,a\bmod q=x,a\bmod (pq)=x\)。\(p,q\)互质。
欧拉定理
若\(gcd(a,n)=1\),则\(a^{\varphi(n)}\equiv1\pmod n\)
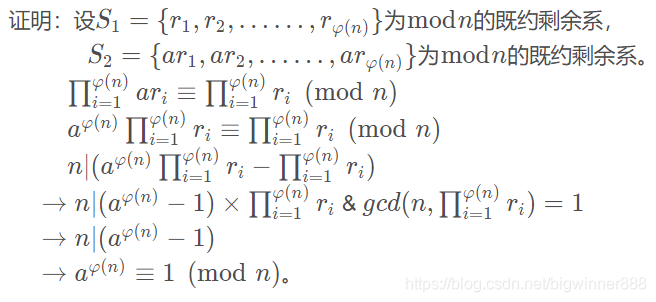
费马小定理
若p为质数,a为整数,有\(a^p\equiv a\pmod p\)
证明:
- \(gcd(a,p)=1\to a^{\varphi(p)}\equiv1\pmod p\)
\(~~\)得\(a^{p-1}\equiv1\pmod p\to a^p\equiv a\pmod p\) - \(gcd(a,p)\neq1\),即a是p的倍数。
\(a^p\%p=0,a%p=0\),即\(a^p\equiv a\pmod p\)。
裴蜀定理(贝祖定理)
对于任意整数a,b,存在一组整数x,y,满足\(ax+by=gcd(a,b)\)
证明:
设\(d=gcd(a,b)\),则\(a=da^{'},b=db^{'}\)
得\(ax+by=da^{'}x+db^{'}y=d(a^{'}x+b^{'}y)=d\),
因为 \(a^{'},b^{'},x,y\)都是整数,
所以只有\(ax+by=gcd(a,b)\)或是\(gcd(a,b)\)得倍数时有解。

扩展欧几里得的通解
对于ax+by=gcd(a,b),通过扩欧得出一组通解\(x_0,y_0\)
得通解:\(x=x_0+b÷gcd(a,b)\times t\)
\(~~~~~~~~~~~~~y=y_0-a÷gcd(a,b)\times t\)
到这里数论的知识就差不多了吧(尽管我还没写中国剩余定理呢)!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号