KMP算法

KMP

KMP算法是一种改进的字符串匹配算法，
由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，
因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）

其实KMP算法就是在BF（暴力算法）上的一个优化，
以避免文本串当前匹配指针回溯的情况来提高时间效率。

实现过程：

在学习KMP算法前，需要理解一个KMP中的避免回溯的方法，NEXT数组。

首先摆出两个概念：
前缀：指的是字符串的子串中从原串最前面开始的子串，如abcdef的前缀有：a,ab,abc,abcd,abcde
后缀：指的是字符串的子串中在原串结尾处结尾的子串，如abcdef的后缀有：f,ef,def,cdef,bcdef

那next数组存的就是一个子串的前缀和后缀的最大交集，
简单来讲就是前缀和后缀的最长相同部分。

"A"的前缀和后缀都为空集，共有元素的长度为0；

"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

---

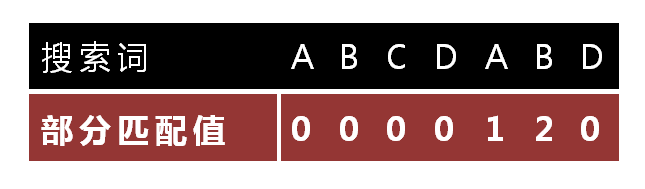
接着讲讲在KMP匹配中NEXT的用法以便加深的它的理解。

当你求出了 next 数组之后，KMP 算法就很轻易搞定了，
下面我用三张图，让你明白 KMP 算法完成匹配的整个过程。
以目标串：s，指针为 i ；模式串：t 指针为 j ; 为例:

上图表示：\(“s_{i-j}\) ~ \(s_{i-1}” == “t_0\) ~ \(t_{j-1}”，s_i != t_j（前面都相等，但比较到 t_j 时发现不相等了）且next[j] == k。\)

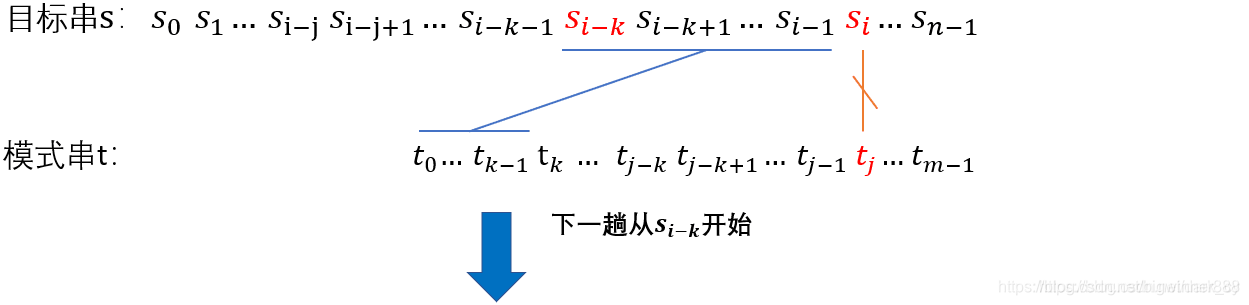
根据 next 数组的定义得知 “\(t_k\) ~ \(t_{ j-1}” == “t_0\)~ \(t_{k-1}”，所以 “t_0 ~ t_{k-1}” == “s_{i-k}\) ~ \(s_{i-1}”\)

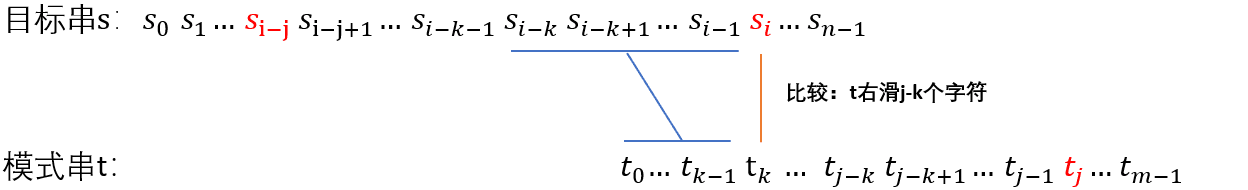
将模式串右移，得到上图，这样就避免了目标穿的指针回溯。

---

现在讲讲Next数组的求法。

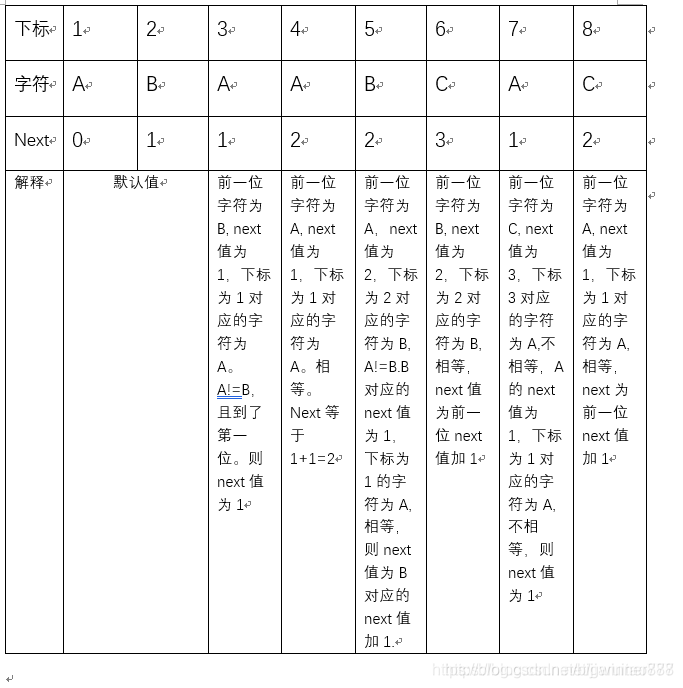
手工求法：

1. 第一二位对应的next值分别为0和1
2. 后面每一位的next值求解：根据前一位进行比较
   • 将前一位的字符 与前一位的next值作为下标对应的字符进行比较
   • 相等，则该位的next值就是前一位的next值加上1
   • 不等，向前继续寻找next值对应的内容来与前一位进行比较，直到找到某个位上内容的next值对应的内容与前一位相等为止，则这个位对应的值加上1即为需求的next值
   • 若找到第一位都不匹配，则改为的next值为1。
     

#include <cstdio>
#include <iostream>
using namespace std;

const int N = 1e6 + 10;
string a, b;
int ans, next[N], l1, l2;

void makeNext()
{
	int len = b.size();
	next[0] = 0;
	for(int i = 1, k = 0; i < len; i++)
	{
		while(k > 0 && b[i] != b[k]) k = next[k - 1];
		if(b[i] == b[k]) k++;
		next[i] = k;
	}
}

int main()
{
	cin >> a >> b;
	makeNext();
	l1 = a.size(), l2 = b.size();
	for(int i = 0, j = 0; i < l1; i++)
	{
		while(j && b[j] != a[i]) j = next[j - 1];
		if(b[j] == a[i]) j++;
		if(j == l2) ans++;
	} 
	printf("%d\n", ans);
	return 0;	
} 

关于KMP的例题
KMP例题题解