利用内外参进行视觉测量
一、 实验任务
1.学习利用摄像机内参数对标定图像正畸
2.学习摄像机外参数标定
3.学习利用单应性矩阵对平面内目标进行测量
二、 实验过程
实验平台:MATLAB R2016a Toolbox_calib工具箱
拍摄靶标图像后,进入目录下打开标定工具箱主界面:
进入目录后,Load之前标定的内参:

经查阅资料了解:fc中两个元素,分别为fx、fy:其中fx = f/dx,f为焦距,单位mm;dx表示x方向像素宽度,单位毫米,1/dx 表示x方向1mm内有多少个像素。因此fx表示使用像素来描述x轴方向焦距的长度;fy同理。
在《机器视觉测量与控制》中标定部分这样描述内参:fc中的两个数据分别是kx,ky,即焦距归一化成像平面上的成像点坐标 到 图像坐标的放大系数。 cc为光轴中心点的图像坐标(u0,v0),又称主点坐标,单位为像素。alpha_c为对应于图像坐标v的摄像机的实际Y轴与理想Y轴之间的夹角,单位为弧度。kc为畸变系数1~5。err为将网格角点反投影到图像空间的误差的标准差,单位为像素。
之后进入测量图片的目录,点击标定外参数:

点击角点后:

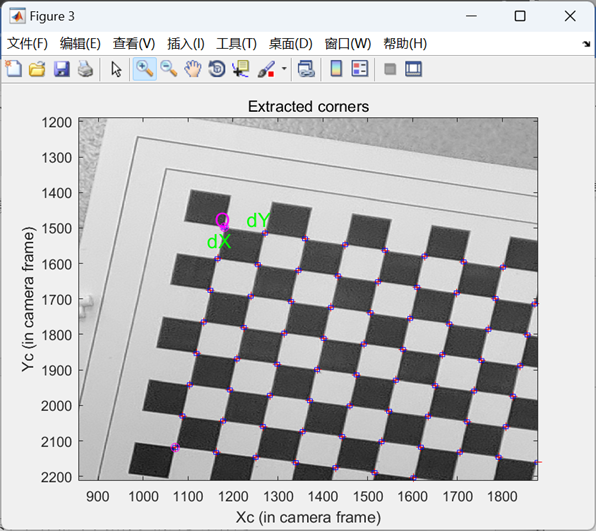
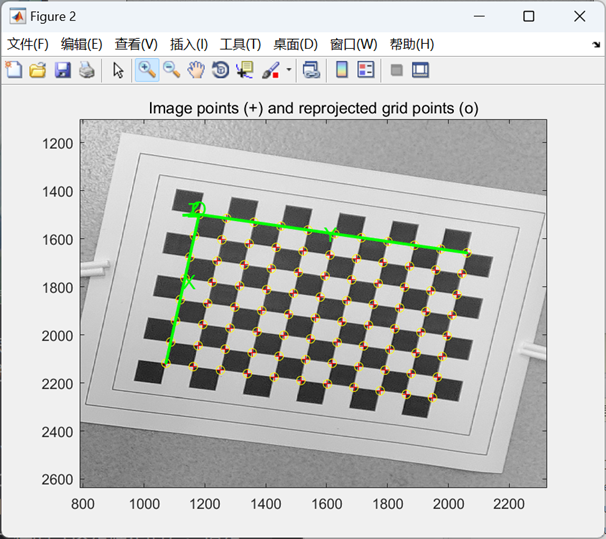
《机器视觉测量与控制》:在外参数标定结果中: Tc_ext 为靶标坐标系原点在摄像机坐标系中的位移向量,单位为 mm; omc_ext 为对应于姿态矩阵的 rodrigues 旋转向量; Rc_ext 为旋转矩阵; err 为将网格角点反投影到图像空间的误差的标准方差,单位为像素。
使用游标观察得到测量的8个点的坐标:

三、 测试过程
计算程序如下:
点击展开Matlab代码
%% import image
% i = imread('IMG8.jpg');
% imshow(i);
%% H matrix
Min = [fc(1),0,cc(1),0; 0,fc(2),cc(2),0; 0,0,1,0];
Mw = [Rc_ext,Tc_ext; 0,0,0,1];
H = Min * Mw;
%% compute the coordinate of A\B\C\D\E\F\G\H
point = [988, 2317, 2125, 808, 1052, 2232, 2068, 897;...
1243, 1494, 2500, 2288, 1334, 1553, 2418, 2228];
m = H/H(3,4);
m1 = [m(1,1)-point(1,1)*m(3,1), m(1,2)-point(1,1)*m(3,2); m(2,1)-point(2,1)*m(3,1), m(2,2)-point(2,1)*m(3,2)];
m2 = [m(1,1)-point(1,2)*m(3,1), m(1,2)-point(1,2)*m(3,2); m(2,1)-point(2,2)*m(3,1), m(2,2)-point(2,2)*m(3,2)];
m3 = [m(1,1)-point(1,3)*m(3,1), m(1,2)-point(1,3)*m(3,2); m(2,1)-point(2,3)*m(3,1), m(2,2)-point(2,3)*m(3,2)];
m4 = [m(1,1)-point(1,4)*m(3,1), m(1,2)-point(1,4)*m(3,2); m(2,1)-point(2,4)*m(3,1), m(2,2)-point(2,4)*m(3,2)];
m5 = [m(1,1)-point(1,5)*m(3,1), m(1,2)-point(1,5)*m(3,2); m(2,1)-point(2,5)*m(3,1), m(2,2)-point(2,5)*m(3,2)];
m6 = [m(1,1)-point(1,6)*m(3,1), m(1,2)-point(1,6)*m(3,2); m(2,1)-point(2,6)*m(3,1), m(2,2)-point(2,6)*m(3,2)];
m7 = [m(1,1)-point(1,7)*m(3,1), m(1,2)-point(1,7)*m(3,2); m(2,1)-point(2,7)*m(3,1), m(2,2)-point(2,7)*m(3,2)];
m8 = [m(1,1)-point(1,8)*m(3,1), m(1,2)-point(1,8)*m(3,2); m(2,1)-point(2,8)*m(3,1), m(2,2)-point(2,8)*m(3,2)];
result = zeros(2,8);
result(:,1) = inv(m1)*(point(:,1) - [m(1,4);m(2,4)]);
result(:,2) = inv(m2)*(point(:,2) - [m(1,4);m(2,4)]);
result(:,3) = inv(m3)*(point(:,3) - [m(1,4);m(2,4)]);
result(:,4) = inv(m4)*(point(:,4) - [m(1,4);m(2,4)]);
result(:,5) = inv(m5)*(point(:,5) - [m(1,4);m(2,4)]);
result(:,6) = inv(m6)*(point(:,6) - [m(1,4);m(2,4)]);
result(:,7) = inv(m7)*(point(:,7) - [m(1,4);m(2,4)]);
result(:,8) = inv(m8)*(point(:,8) - [m(1,4);m(2,4)]);
%% compute the length of AB......
len_AB = ((result(1,1)-result(1,2))^2 +...
(result(2,1)-result(2,2))^2)^0.5
len_CD = ((result(1,3)-result(1,4))^2 +...
(result(2,3)-result(2,4))^2)^0.5
len_BC = ((result(1,2)-result(1,3))^2 +...
(result(2,2)-result(2,3))^2)^0.5
len_DA = ((result(1,4)-result(1,1))^2 +...
(result(2,4)-result(2,1))^2)^0.5
len_EF = ((result(1,5)-result(1,6))^2 +...
(result(2,5)-result(2,6))^2)^0.5
len_GH = ((result(1,7)-result(1,8))^2 +...
(result(2,7)-result(2,8))^2)^0.5
len_FG = ((result(1,6)-result(1,7))^2 +...
(result(2,6)-result(2,7))^2)^0.5
len_HE = ((result(1,8)-result(1,5))^2 +...
(result(2,8)-result(2,5))^2)^0.5
经过测量得到如下表格:
| 角点 | 图像坐标/像素 | 位置/mm | 边 | 测量长度/mm | 相对误差 |
|---|---|---|---|---|---|
| A | 988;1243 | (-71.87,-76.80) | AB | 453.14 | 0.7% |
| B | 2317;1494 | (-68.17,365.46) | CD | 453.51 | 0.78% |
| C | 808;2288 | (-271.81,-360.85) | BC | 352.99 | 0.85% |
| D | 2125;2500 | (-280.15,-75.33) | DA | 353.21 | 0.92% |
| E | 1052;1334 | (-280.15,-75.34) | EF | 402.57 | 0.64% |
| F | 2232;1553 | (-280.15,-75.35) | GH | 402.95 | 0.74% |
| G | 2068;2418 | (-280.15,-75.36) | FG | 302.89 | 0.96% |
| H | 897;2228 | (-280.15,-75.37) | HE | 302.83 | 0.94% |
四、 总结部分
首先已知小孔成像的相似三角形关系。
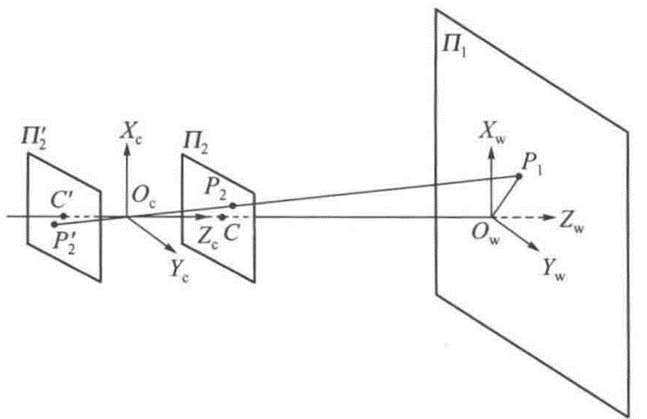
物点P1,成像点P2:x1/z1 = x2/f; y1/z1 = y2/f;
光轴中心点的图像坐标(u0, v0);(畸变是指此处有系数变化)
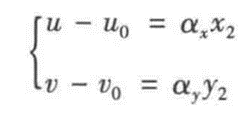
α表示成像点到图像点的放大系数,即一个像素代表mm分之一;
带入上面的x2,y2:
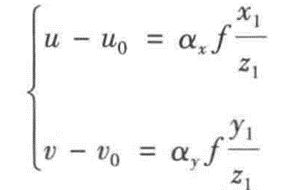
得到内参公式:
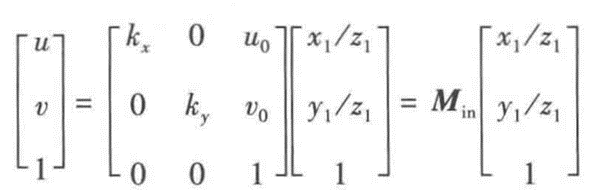
其中kx = αxf,表示焦距有多少个像素点;
(x1, y1, z1)是物点在摄像机坐标系下的坐标(一般用zc表示);
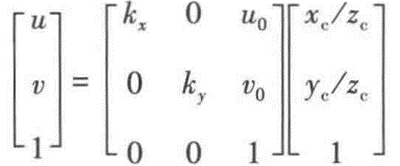
外参公式比较容易:R为从世界坐标旋转到相机坐标的旋转矩阵,p为世界坐标原点在摄像机坐标中的位置。
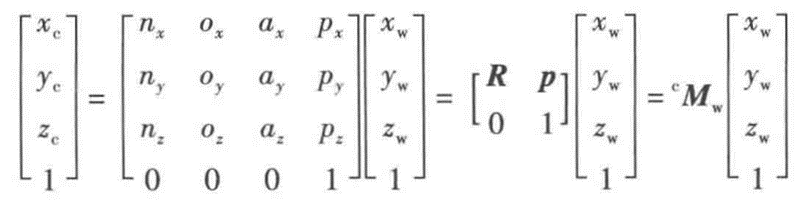
综上:将物点像素u,v, 1乘zc得到内外参矩阵 × 物点在世界坐标系的坐标:
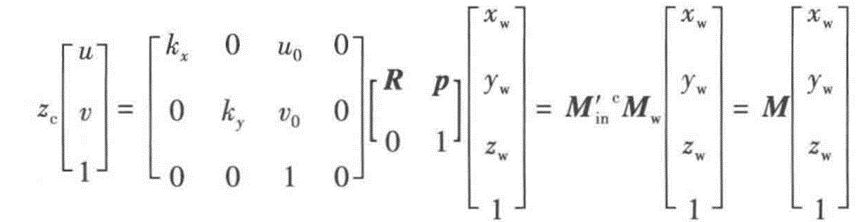
注意:zc不是一个固定的值,而是每个点有其自己的系数!!
得知了以上图像与世界坐标关系,就可以计算了:
首先将内外参矩阵写为一个矩阵M:
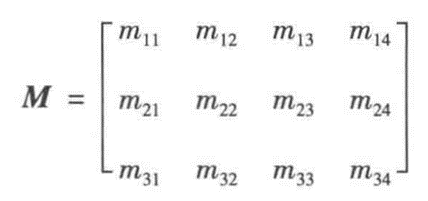
带入图像与世界坐标关系方程:
Zcu = m11xw + m12yw + m13zw +m14
Zcv = m21xw + m22yw + m23zw +m24
Zc = m31xw + m32yw + m33zw +m34
可以把zc带入其他两个式子:
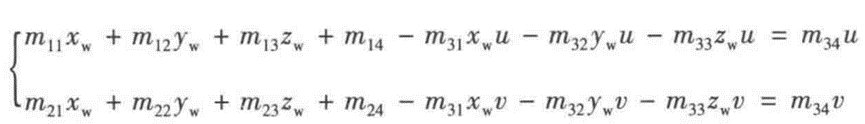
考虑到实验中,物点与世界坐标xy平面共面,所以zw = 0:
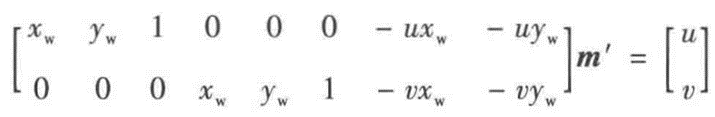
其中上式中的m‘ = [m11; m12; m14; m21; m22; m24; m31; m32] / m34
于是将上式拆开,将世界坐标拿出来,好计算平面内的二维坐标:
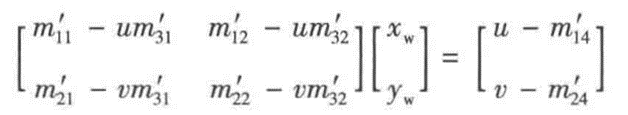
对每个像素点分别解方程,得到其世界坐标即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号