第六章学习小结

1.图的相关定义和术语

　　关于这部分，在离散数学里面有重点学，所以只强调几个特殊的点：

　　如果一个图有 n 个顶点和小于 n-1 条边，则是非连通图。

　　无向完全图和有向完全图：对千无向图，若具有 n(n- 1)/2 条边，则称为无向完全图。 对于有向图，若具有n(n- l)条弧，则称为有向完全图。

　　连通图的生成树： 一个极小连通子图，它含有图中全部 顶点，但只有足以构成一棵树的 n-1条边，这样的连通子图称为 连通图的生成树。

　　有向树和生成森林：有一个顶点的入度为 0, 其余顶点的入度均为 l 的有向图称为有向 树。 一个有向图的生成森林是由若干棵有向树组成，含有图中全部顶点，但只有足以构成若干棵 不相交的有向树的弧。

2.图的存储

　　（1）邻接矩阵表示法（以边集合方式表示）：数据结构包含三个成员：存储顶点信息的一位数组顶点表vexs[ ]、存储边的信息的邻接矩阵(二维数组)arcs[ ][ ]、图的点数vexnum和边数arcnum。

　　　　关于邻接矩阵：尺寸：n*n的方阵，n为图的顶点个数。其中元素A[i][j]的值为0或1，当值为0时，表示<i,j>没有边连接，如果是有向图<i,j>表示从i指向j的边，<i,j>与<j,i>不相同。当值为1时，则表明<i,j>

　　　　<i,j>有边。

　　　　如果表示的是网，对应的值存储的则是边的权值，此时，如果值是无穷，则表明没有边相连。所以在初始化网的时候要先将所有边初始化为INT_MAX。

　　　　优点：方便判断两个顶点间有无边、便于计算某个顶点的度。

　　　　缺点：不方便用以增加和删除点、难统计边的数目、空间复杂度高。

　　（2）邻接表表示法（以链接方式表示）：数据结构成员：①边结点：指向顶点的位置、指向下一条边的指针、和边相关的信息（例：权值）。②顶点结点：顶点编号、指向第一条依附该顶点的边的指针。

　　　　③邻接表：顶点结点数组、图的边数和顶点数。

　　　　优点：便于增加或删除顶点、便于统计边的数目、空间效率高。

　　　　缺点：不便于判断某两个顶点间是否有边、不便于计算顶点的度。

　　　　十字链表、邻接多重表不常用。

　　引用书上一张很详细的表

　　

 

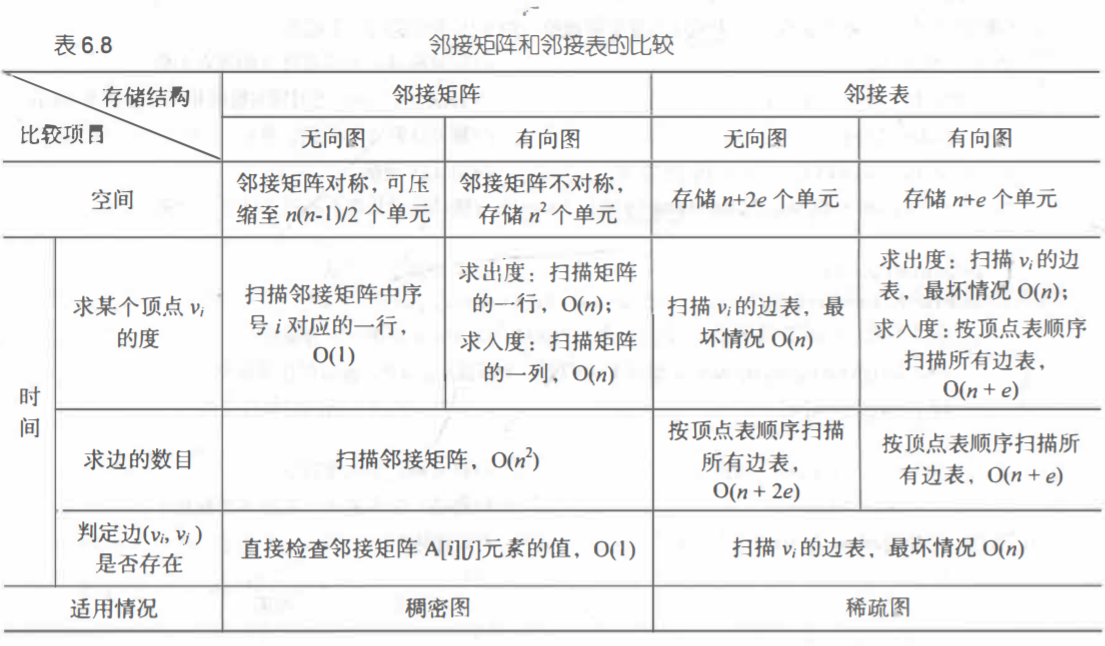
3.图的遍历

　　（1）深度优先搜索（DFS）：类似树的先序遍历过程。

　　　　过程：①从某个顶点v1开始出发。②找出刚访问过的顶点的第一个未被访问的邻接点， 访问该顶点。 以该顶点为新顶点，重 复此步骤， 直至刚访问过的顶点没有未被访问的邻接点为止。

　　　　　　　③返回前一个访问过的且仍有未被访问的邻接点的顶点，找出该顶点的下一个未被访问的 邻接点， 访问该顶点。④重复步骤 (2) 和(3), 直至图中所有顶点都被访问过，搜索结束。

　　　　伪代码：

　　　　void DFS(起始节点 V)

　　　　{

　　　　　　　将起始节点V标记拜访过

　　　　　　　for(V节点的所有邻接节点W)

　　　　　　　{

　　　　　　　　if(邻接节点W没有拜访过)

　　　　　　　　　递归调用DFS(邻接节点W)

　　　　　　　}

　　　　}

　　　　　示例代码：

void DFSTraverse(Graph G)
{//对非连通图G做深度优先遍历
    for(v=O;v<G.vexnum;++v) visited[v]=false;//访问标志数组初始化
    for(v=O;v<G.vexnum;++v)/
        if(!visited[v]) DFS(G,v); ／／对尚未访问的顶点调用DFS
}

 

 　　（2）广度优先搜索（BFS）：

　　　　过程：①从图中某个顶点v出发，访问v。②依次访问v的各个未曾访问过的邻接点。③分别从这些邻接点出发依次访问它们的邻接点， 并使 “先被访问的顶点的邻接点“ 先于 ”后被访问的顶点的邻接点”

　　　　被访问。重复步骤(3), 直至图中所有已被访问的顶点的邻接点都被访问到。

　　　　伪代码：

　　　　void BFS(起始节点 V)
　　　　{
　　　　　将起始节点V标记拜访过
　　　　　将起始节点V压入队列Q
　　　　　while（队列Q不空）
　　　　　{
　　　　　　队列Q弹出一个元素W
　　　　　　for(元素W的所有邻接节点T)
　　　　　　{
　　　　　　　　if(节点T没有被拜访过)
　　　　　　　　{
　　　　　　　　　　将节点T标记拜访过
　　　　　　　　　　将节点T压入队列Q
　　　　　　　　}
　　　　　　}
　　　　　}
　　　　}

　　　　示例代码：

void BFS{Graph G,int v)
{//按广度优先非递归遍历连通图G
    cout<<v;visited[v]=true;//访问第v个顶点，并置访问标志数组相应分址值为true
    InitQueue{Q); //辅助队列Q初始化， 置空
    EnQueue(Q,v); //v进队
    while {! QueueEmpty (Q)}//队列非空
    {
        DeQueue (Q, u); //队头元素出队并置为u
        for(w=FirstAdjVex(G,u);w>=0;w=NextAdjVex(G,u,w)) 
        {//依次检查u的所有邻接点w, FirstAdjVex(G,u)表示u的第一个邻接点
         //NextAdjVex(G,u,w)表示u相对于w的下一个邻接点，w>=0表示存在邻接点
             if (!visited [w])//w为u的尚未访问的邻接顶点
            {
                cout<<w; visited[w]=true;//访问 w, 并置访问标志数组相应分扯值为true
                EnQueue (Q, w) ;//w进队
            }
          }
    }
}

4.图的相关算法

　　（1）构造最小生成树：①Prim算法：归并点，时间复杂度O(n^2)，适用于稠密网。②Kruskal算法：归并边，时间复杂度O(e*log2(e))适用于稀疏网。

　　（2）最短路径：Dijkstra算法：时间复杂度O(n^2)。