第五章学习小结

第五章讲的是树和二叉树。

1.二叉树是最常用的树结构，二叉树中又包含了满二叉树和完全二叉树。

　　满二叉树：每一层上的结点数都是最大结点数，即每一层l的结点数都具有最大值2^(i-1)

　　完全二叉树：深度为K的， 有n个结点的二叉树， 当且仅当其每一个结点都与深度为K的满 二叉树中编号从1至n的结点一一对应时， 称之为完全二叉树。

2.关于二叉树的存储、性质。

　　二叉树同样也有两种存储形式，链式存储和顺序存储。但是顺序存储的限制性较大，只能适用于完全二叉树，而且当完全二叉树空元素比较多的时候会浪费比较多的空间。

　　相对来说，二叉树更常用的是链式存储结构。而根据不同的二叉树的特点，又可以构建出很多二叉树链式结构。比如：包含指向双亲和孩子的指针的结点构成的链表、只包含指向孩子指针的结点，

　　分别叫做三叉链表和二叉链表。

　　主要性质：

　　1.在二叉树的 第l层上至多有2^(i-1)个结点

　　2.深度为K的 二叉树至多有 2^k-1个结点 (k>=1)

　　3.对任何一棵二叉树T, 如果其终端结点数为n0，度为2的结点数为n2,则n0 = n2+1。

3.二叉树的遍历

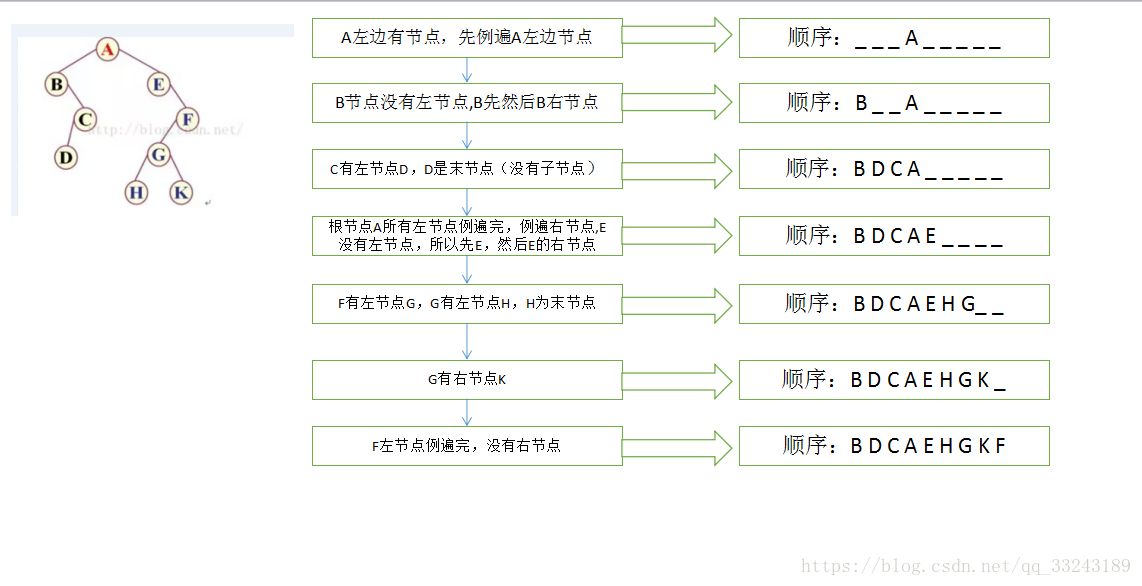
　　有一说一，这部分当时听课是真的没搞懂，后面看到网上的解释才完全了解了。下面引用一张网上解释很清晰的图来类比前序、后序遍历。

　　

4.哈夫曼树

 

　　哈夫曼树也称为最优树，主要应用在通信部分，在通信的时候，构建哈夫曼树来传输信息是最快的。

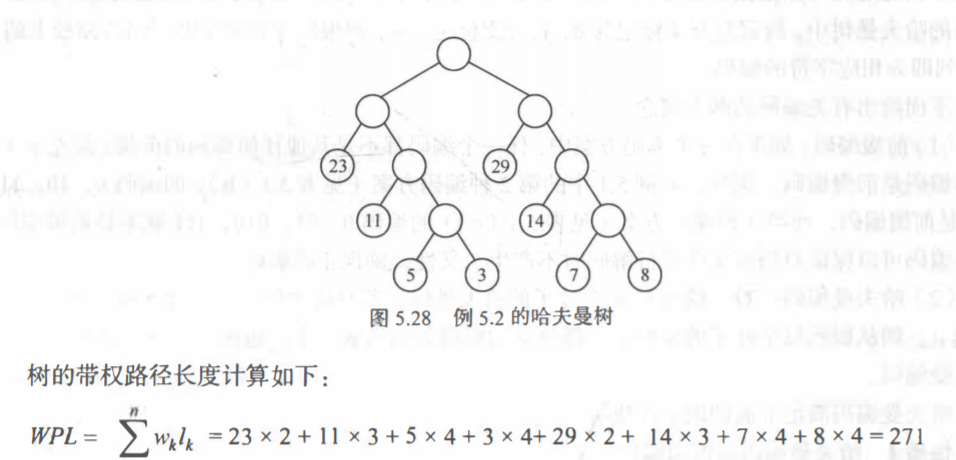
　　哈夫曼树每个结点包括这个结点的权重、双亲、左右孩子的下标。然后存储在一个动态数组中。重点要掌握的是WPL值的算法：根据路径长度乘以结点的权重。

 

 

5.数和森林

　　普通数一般有两种表示方式：双亲表示法和孩子兄弟表示法。若干棵树可以组成一个森林，将每一棵树用孩子兄弟表示法表示之后，再用同样的方法相连即是森林。

6.关于二叉数的算法

　　许多关于二叉树的算法都是用递归实现的，例如：

　　1.求二叉树的叶子结点

int leaf(bitTree T)
{
    if(T == NULL) return 0;
    else if(T->lchild == NULL && T->rchild == NULL) return 1;
    else
    {
        return leaf(T->lchild) + leaf(T->rchild);
    }
}

　　2.中序遍历

void inorder(bitTree T)
{
    if(T!=NULL)
    {
        inorder(T->lchild);
        cout << T->data;
        inorder(T->rchild);
    }
}

　　3.创建二叉树

void creat(bitTree &T)
{
    char ch;
    cin >> ch;
    if(ch == '#') T = NULL;
    else
    {
        T = new bitNode;
        T->data = ch;
        creat(T->lchild);
        creat(T->rchild);
    }
}