COMP3357 tutorial: 中国剩余定理 (Chinese Remainder Theorem) 与整数模 p 乘法群

中国剩余定理 Chinese Remainder Theorem (CRT)

Definition

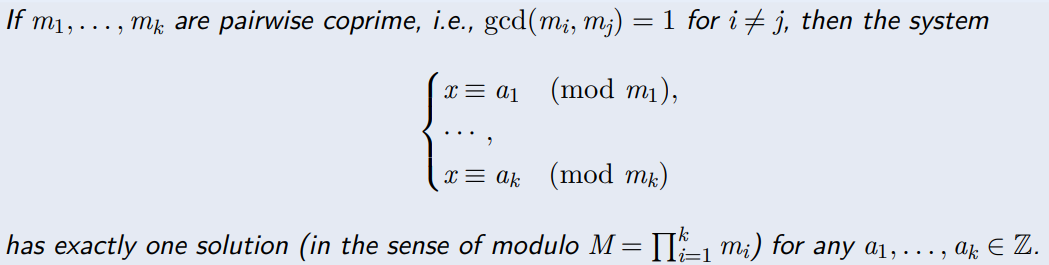
Points to Note:

• 方程组的模数 \(m_1,m_2,...,m_k\) 是两两互质 (pairwise coprime) 的
• 该方程组的解 \(x\) 在模 \(M=\prod m_i\) 意义下是唯一的 (也就是说，所有的解 \(x\) 模 \(N\) 等价)
• 该方程组的解是 \(x=\sum_{i=1}^k a_iM_it_i\mod{M}\)，其中 \(M_i=M/m_i\), \(t_i=M_i^{-1}\pmod{m_i}\)

Proof

CRT 是正确的，我们需要证明

• 解的存在性 (existence)
  对于方程组:
  
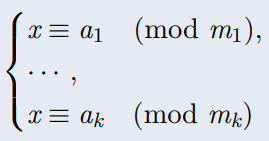
  \(M=\prod_{i=1}^k m_k\)，我们令 \(M_i=M/m_i\) (\(M_i\) 为除 \(m_i\) 外所有模数的积)
  令 \(t_i\) 为 \(M_i\) 模 \(m_i\) 下的逆元，即 \(M_it_i\equiv 1\pmod{m_i}\)
  我们能够构造解 \(x=\sum_{i=1}^k a_iM_it_i\): 因此，任意解 \(x_0\equiv x\pmod{M}\)

  • 解的正确性
    对于方程组中的第 \(j\) 个方程 \(x\equiv a_j\pmod{m_j}\)
    \(x=a_1M_1t_1+a_2M_2t_2+...+a_jM_jt_j+...a_kM_kt_k\)
    对于所有 \(i\neq j\) 的项 \(a_iM_it_i\)，\(M_i=M/m_i\)，所以 \(M_i\) 一定包含 \(m_j\) (即 \(m_j|M\))，因此 \(a_iM_it_i\equiv 0\pmod{m_j}\)
    而 \(a_jM_jt_j\equiv a_j \pmod{m_j}\) since \(M_jt_j\equiv 0\pmod{m_j}\)

• 解的唯一性 (uniqueness)
  若 \(x,x'\) 均为方程组的解，那么 \(\forall i\in[1,k]\)，都有 \(x\equiv a_i\pmod{m_i}\), \(x'\equiv a_i\mod{m_i}\)
  因此 \(x\equiv x'\pmod{m_i}\), 或是说 \(m_i|x-x'\)
  因为 \(m_1,m_2,...,m_k\) are pairwise coprime, \(M|x-x'\), i.e., \(x\equiv x'\pmod{M}\)
  所以 \(x,x'\) 模 \(M\) 同余，方程在模 \(M\) 意义下有唯一解

Application

• 简化 \(a^e\mod{M}\) 的计算
  对于 prime \(M\), \(a^e\mod{M}\) 能够用 Fermat's little Theorem 或者 Euler's Theorem 来化简
  对于 composite \(M\)，但 \(\gcd(M, a)=1\) 的情况，Euler's Theorem 仍然适用
  而对于 composite \(M\) 但 \(\gcd(M,a)\neq 1\) 的情况，就需要借助 CRT 进行简化
  

• Accelerate RSA Decryption
  

关于整数模 \(p\) 乘法群 \(\Z_p^*\) 的研究

循环群的定义

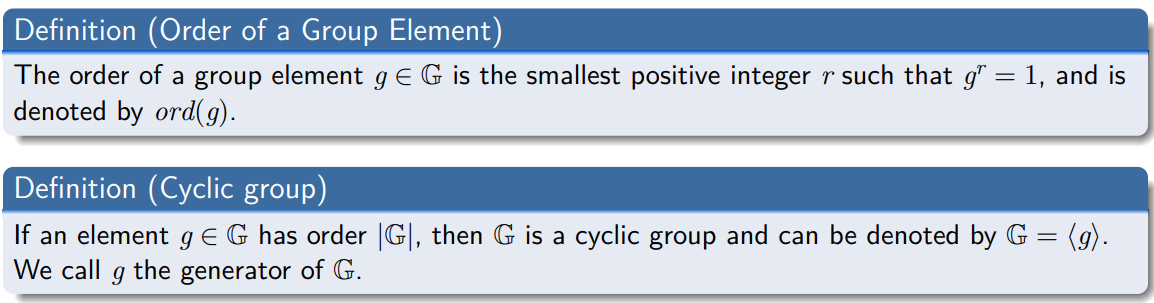
有生成元 generator 的群就是循环群

\(\Z^*_p\) 是一个循环群

\(\Z^*_p\) for some prime \(p\) 是一个经典的循环群，下面我们将对其进行证明

• \(ord(g)|\varphi(p)\)
  我们先证明，对于任何 \(g\in Z^*_p\)，都有 \(ord(g)|\varphi(p)\)
  \(g^{ord(g)}\equiv 1\pmod{p}\)
  \(g^{\varphi(p)}\equiv 1\pmod{p}\)
  且 \(ord(g)\) 是 smallest positive integer \(r\) s.t. \(g^r\equiv 1\mod{p}\)，所以一定有 \(ord(g)\leq \phi(p)\)
  所以 \(ord(g)|\varphi(p)\)

• 欧拉函数性质 \(\sum_{d|n} \varphi(d)=n\)
  这个结论好熟悉！就是之前学过的迪利克雷卷积 \(\varphi * \mathtt{1}= \mathtt{Id}\) 的展开形式
  证明有点靠直觉: 我们将所有以 \(n\) 为分母的分式写出来 \(\frac{1}{n}, \frac{2}{n}, ..., \frac{n}{n}\) 并化简成最简形式 (Simplified forms)
  写成化简形式后，这些分式的分母 \(\in \{d \ \mathtt{s.t.} d|n\}\) (即所有的分母一定都是 \(n\) 的 divisor)
  对于一个分母为 \(d\) 的分式，其分子有 \(\varphi(d)\) 种 (分子与分母必须互质，否则还可以继续化简)
  所以，\(\forall d \ \mathtt{s.t.} d|n\)，其都占有 \(\{\frac{1}{n}, \frac{2}{n}, ..., \frac{n}{n}\}\) 中的 \(\varphi(d)\) 个分式
  那么 \(\sum_{d|n} \varphi(d)=n\)

• Proof (incomplete)
  我们定义函数 \(F(r)\) 为 \(\Z^*_p\) 中，阶为 \(r\) 的元素的个数
  由 \(ord(g)|\varphi(p)\) 我们知道，所有元素的阶一定是 \(\varphi(p)\) 的 divisor
  所以有: \(\sum_{d|\varphi(p)} F(d)=|\Z^*_p|=\varphi(p)\)
  又根据 \(\varphi * \mathtt{1}= \mathtt{Id}\) 有 \(\sum_{d|\varphi(p)} \varphi(d)=\varphi(p)\)
  因此 \(\sum_{d|\varphi(p)} F(d)=\varphi(p)=\sum_{d|\varphi(p)} \varphi(d)\)
  我们得到当 \(p\) 为质数时, \(F(d)=\varphi(d)\)
  (这里的结论得出是不完整的，我们还需要通过 Lagrange's Theorem 证明 \(F(d)\leq \varphi(d)\) 后得出 \(F(d)=\varphi(d)\)，但该证明比较复杂，故直接取这个符合直觉的结论)

• 生成元的个数
  有了 \(F(d)=\varphi(d)\) 这一关系后，我们可以求出 \(\Z^*_p\) 中阶为 \(r\) 的元素个数 \(\varphi(r)\)
  那么根据生成元的定义 (阶为 \(\varphi(p)\) 的元素)，我们可以得到 \(\Z^*_p\) 有 \(\varphi(\varphi(p))=\varphi(p-1)\) 个生成元
  从而证明若 \(\varphi(p-1)\neq 0\)，\(\Z^*_p\) 是一个循环群

原根与整数模 \(n\) 乘法群

• 原根 (primitive root)
  对于整数模 \(p\) 乘法群 (\(p\) is prime) \(\Z^*_p\)，我们已经证明其一定是循环群
  那么，对于这一类群，我们将其的生成元 (generator) 又称作原根 (primitive root): 质数 \(p\) 的原根，即群 \(\Z^*_p\) 的生成元
  目前没有求原根的一般方法 (general methods)，但是在所有 \(\varphi(p)\) 个元素中有 \(\varphi(\varphi(p))\) 个原根，使用随机化算法也能够 efficiently 得到原根

• 其他整数模 \(n\) 乘法群 \(\Z^*_n\)
  当 \(n\) 不是质数时，需要满足什么条件能够使得 \(\Z^*_n\) 是循环群？
  答案: (\(2\)), \(4\), \(p^k\), \(2p^k\) (\(p\) 是一个奇质数，\(k\) 是一个正整数)

二次剩余 Quadratic Residue

这里简单的对二次剩余做一点总结，虽然在这堂课里着墨不多，但是在数论领域还是一个很经典的问题

二次剩余问题

一个数 \(a\)，如果不是 \(p\) 的倍数且模 \(p\) 同余于某个数的平方，则称 \(a\) 为模 \(p\) 的 二次剩余 (quadratic residue)。
而一个数 \(b\)，如果不是 \(p\) 的倍数且模 \(p\) 不同于任何数的平方，则称 \(b\) 为模 \(p\) 的 二次非剩余 (quadratic nonresidue)

对二次剩余求解，即对常数 \(a\) 解方程: \(x^2\equiv a \pmod{p}\)
通俗来讲，即是进行 模意义下的开平方运算 (find e-th root modulo \(p\) 的特殊情况: \(e=2\))
在研究二次剩余问题时，模数 \(p\) 一般是奇质数

Legendre 符号

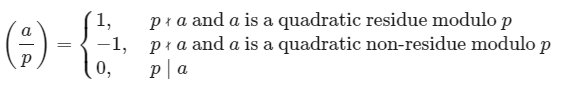
引入勒让德符号 \((\frac{a}{p})\)，标记 \(a\) 是否是模 \(p\) 的二次剩余

Euler 判别准则

对于奇素数 \(p\) 与 \(p\not| a\) 有

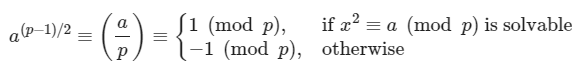
欧拉判别准则指出，我们可以直接通过计算 \(a^{(p-1)/2}\) 计算 \(a\) 模 \(p\) 的勒让德符号
这里是证明 (from OI wiki)，很简明易懂

Tutorial questions

Hastad 广播攻击 (Håstad's broadcast attack)

首先看到三个方程，不同模数就联想到 CRT: 列出方程组

但是，CRT 的应用条件是模数两两互质。讨论

• \(\gcd(N_i, N_j)\neq 1\) for some \(1\leq i\leq j\leq 3\):
  这种情况下，我们能够成功的找到 \(N_i\) 与 \(N_j\) 的 factorization
  若 \(\gcd(N_i, N_j)=p\), 则 \(d_i=e^{-1}\mod{\varphi(N_i)}=d^{-1}\mod{(p-1)(N_i/p-1)}\)
  得到 \(d_i\) 后，解密 \(m\) 就十分简单了
• \(\gcd(N_i, N_j)=1\) for all \(1\leq i\leq j\leq 3\):
  这种情况下，我们直接进行 CRT 求解
  \(m^3\equiv \sum_{i=1}^3 a_iM_it_i \pmod{N_1N_2N_3}\)
  由于在 Plain RSA 中，\(m< N_i\) for all \(i\)，所以 \(m^3<N_1N_2N_3\)
  我们只需要进行整数开根 \(\sqrt[3]{\sum_{i=1}^3 a_iM_it_i}\) 即可 recover \(m\)

DDH Assumption fails when using \(\Z^*_p\)

若 \(g\) 是 \(\Z^*_p\) 的生成元，\(h\in \Z^*_p\)，则一定存在 \(x\) 使 \(g^x=h\)
\(x\) 的奇偶性 (parity) 可以通过计算 \(h\) 是否是模 \(p\) 的二次剩余来确定、

• \(x\) is even, 则 \(x=2t\), \((\frac{h}{p})\equiv g^{2t\cdot(p-1)/2}\equiv(g^{p-1})^t\equiv1\pmod{p}\)，因此 \(h\) 是模 \(p\) 的二次剩余
• \(x\) is odd, 则 \(x=2s+1\), \((\frac{h}{p})\equiv g^{2s\cdot (p-1)/2}g^{(p-1)/2}\equiv 1\cdot (-1)\equiv -1\pmod{p}\), 因此 \(h\) 是模 \(p\) 的二次非剩余

这一结论可以用于攻破使用 \(\Z^*_p\) 的 DDH 问题
给出 \(g, g^x, g^y, h=g^z\), 当 \(h\) 是模 \(p\) 的二次剩余时，敌手 \(\mathscr{A}\) 输出 \(1\)，否则输出 \(0\)

• \(h=g^z=g^{xy}\)，由于 \(x,y\) 都是随机的，因此 \(xy\) 的奇偶可能性为 \(\mathtt{odd}:\mathtt{even}=1:3\)
  于是有 \(\Pr[(\frac{h}{p})=1]=\Pr[z \ \mathtt{is} \ \mathtt{even}]=3/4\)
• \(h=g^z\) for some uniform \(z\)，因此 \(z\) 的奇偶可能性为 \(mathtt{odd}:\mathtt{even}=1:1\)
  于是有 \(\Pr[(\frac{h}{p})=1]=\Pr[z \ \mathtt{is} \ \mathtt{even}]=1/2\)

这样 \(|\Pr[\mathscr{A}(Z_p^*, q, g, g^x, g^y, g^z)=1]-\Pr[\mathscr{A}(Z_p^*, q, g, g^x, g^y, g^{xy})=1]|=1/4\)，而这个概率是 non-negligible 的
所以 DDH Assumption fails when using \(\Z^*_p\)，自然，使用 \(Z^*_p\) 的任何 Diffie-Hellman 密钥交换协议与 El Gamel 加密都是不安全的

一些常用的能保证 DDH Assumption 的群:

本文中所有引用来自 OI wiki 与 TA Zhang Chengru 的 PPT Slide