1.9寒假集训-进阶训练赛（五）A-M题解

前五题网上都有不写了

需要注意的是第四题是给定密钥和密文要把它加密算是一个逆过程看了半天都没读懂样例

第六题应该也有但是我写一下因为学校oj这边空间给的是128mb 蓝桥杯正常应该是给256 直接设f[i][j]表示前i个可以组成j的话空间不太够

所以我们用一个滚动数组即可算是一个小技巧吧

#include<bits/stdc++.h>
using namespace std ;
#define maxn 110100
#define int long long
int read(){
    int ans = 0 , f = 1 ; char ch = getchar() ;
    while ( !isdigit(ch) ){ if( ch == '-' ) f = -1 ; ch = getchar() ; }
    while ( isdigit(ch) ) ans = (ans * 10) + (ch ^ '0') , ch = getchar() ;
    return ans * f ;
}
int f[5][maxn] ;
int n , w[maxn] ;  
signed main(){
//    freopen("test.in" , "r" , stdin) ;
//    freopen("test.out" , "w" , stdout) ;
    n = read() ; 
    f[0][0] = 1; int now = 1 ; 
    for(int i = 1 ; i <= n ; i++){
        w[i] = read() ; 
        f[now][0] = 1 ; 
        for(int j = w[i] ; j <= 100000 ; j++){
            f[now][j] |= f[now ^ 1][j]; 
            f[now][j] |= f[now ^ 1][j - w[i]] ;
            f[now][j] |= f[now ^ 1][j + w[i]] ; 
        }
        for(int j = 1 ; j < w[i] ; j++){
            f[now][j] |= f[now ^ 1][w[i] - j] ; f[now][j] |= f[now ^ 1][j] ; 
            f[now][j] |= f[now ^1][j + w[i]] ; 
        }
        now ^= 1 ; 
    }
    now ^= 1 ; 
    int ans = 0 ; 
    for(int i = 1 ; i <= 100000 ; i++)
        ans += f[now][i] ; 
    printf("%lld" , ans) ; 
    return 0 ;
}

G 最小值

两个数的差大于2019的话肯定可以让一个是2019的倍数不大于2019直接枚举最差情况下是枚举2019²次

#include<bits/stdc++.h>
using namespace std ;
#define maxn 400100
#define int long long
int read(){
    int ans = 0 , f = 1 ; char ch = getchar() ;
    while ( !isdigit(ch) ){ if( ch == '-' ) f = -1 ; ch = getchar() ; }
    while ( isdigit(ch) ) ans = (ans * 10) + (ch ^ '0') , ch = getchar() ;
    return ans * f ;
}
signed main(){
//    freopen("test.in" , "r" , stdin) ;
//    freopen("test.out" , "w" , stdout) ;
    int l = read() , r = read() ; 
    int ans = 999999 ; 
    if(r - l >= 2019){
        printf("0") ; 
        return 0 ; 
    }
    for(int i = l ; i < r ; i++)
        for(int j = i + 1 ; j <= r ; j++)
            ans = min(ans , i * j % 2019) ; 
    printf("%lld" , ans) ; 
    return 0 ;
}

H题感觉有被骂道我错了今晚就开始补题呜呜

n = read() , d = read() ; 
    d = 2 * d + 1 ; 
    printf("%lld" , (n / d + (n % d != 0))) ;

I题模拟即可不需要思考

int n , mx1 , mx2;
multiset<int> s ; 
multiset<int>::iterator it ;
int a[maxn] ;  
signed main(){
//    freopen("test.in" , "r" , stdin) ;
//    freopen("test.out" , "w" , stdout) ;
    n = read() ; 
    for(int i = 1 ; i <= n ; i++)
        a[i] = read() , s.insert(a[i]) ; 
    for(int i = 1 ; i <= n ; i++){
        s.erase(s.find(a[i])) ; 
        it = s.end() ;
        it-- ; 
        printf("%lld\n" , *it) ; 
        s.insert(a[i]) ; 
    }
    return 0 ;
}

J题模拟

int calc(int x){
    int sum = 0; 
    while(x){
        sum++ ;
        x /= 10 ;
    }
    return sum ; 
}
int n ; 
signed main(){
//    freopen("test.in" , "r" , stdin) ;
//    freopen("test.out" , "w" , stdout) ;
    n =read() ; 
    int ans = 0 ; 
    for(int i = 1 ; i <= n ; i++){
        ans += calc(i) % 2 == 1 ; 
    }
    printf("%lld" , ans) ; 
    return 0 ;
}

K题

以样例来说 a[1] + a[2] = A1 * 2

a[2] + a[3] = A2 * 2 a[3] + a[1] = A3 * 2

所以用一式减二式加三式就能得出a[1] 后面递推即可

n = read() ; 
    for(int i = 1 ; i <= n ; i++){
        a[i] = read() ; 
    }
    int a1 = 0 ; 
    for(int i = 1 ; i <= n ; i++){
        if(i %2 == 1)
            a1 += a[i] ; 
        else a1 -= a[i] ; 
    }
    printf("%lld " , a1) ; 
    for(int i = 1 ; i < n ; i++){
        printf("%lld " , a1 = 2 * a[i] - a1) ; 
    }

L题不太理解怎么没什么人写L题正常的模拟一下从树顶开始涂色的过程

这个样例太差劲了我画一个

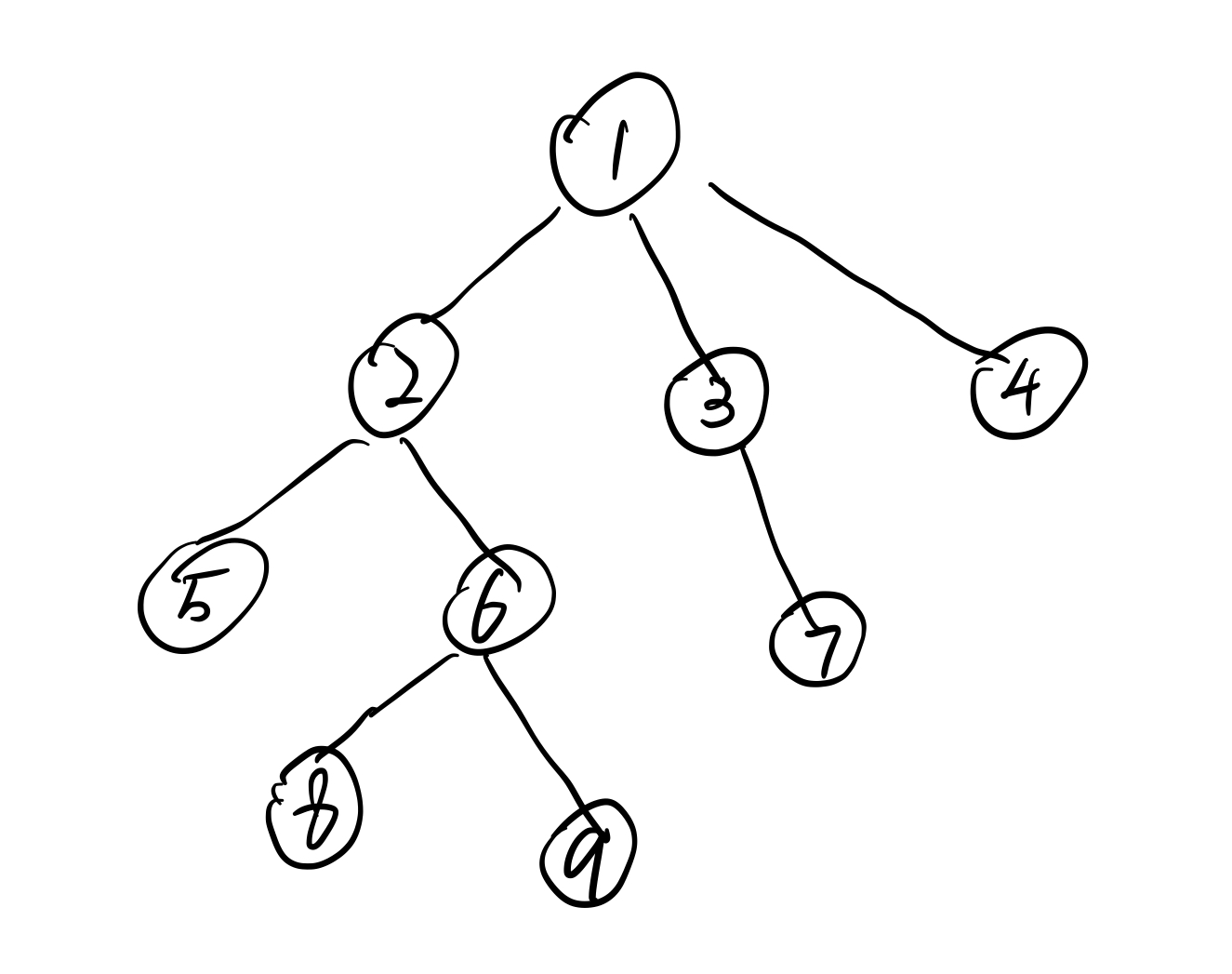
假设k是8好了

首先涂1点有八种情况

然后涂2点 7种情况 3 6种情况 4 5种情况

很明显在同一父节点的情况下考虑一下当前节点是第几个点越靠后的点情况数量越低

然后是第三层的点从第三层开始最多也只能有k-2种了因为第二层不用考虑爷爷结点第三层开始就要了

具体看看代码应该能明白

#include<bits/stdc++.h>
using namespace std ;
#define maxn 400100
#define int long long
int read(){
    int ans = 0 , f = 1 ; char ch = getchar() ;
    while ( !isdigit(ch) ){ if( ch == '-' ) f = -1 ; ch = getchar() ; }
    while ( isdigit(ch) ) ans = (ans * 10) + (ch ^ '0') , ch = getchar() ;
    return ans * f ;
}
int n , k ; 
int val[maxn] ; 
vector<int> G[maxn] ; 
void dfs(int u , int dep , int fa , int numson){
    if(dep == 1){
        val[u] = k ; 
    }
    else if(dep == 2) val[u] = k - 1 - numson ; 
    else val[u] = k - 2 - numson ; 
    int cnt = 0 ; 
    for(int i = 0 ; i < G[u].size() ; i++){
        int v = G[u][i] ; 
        if(v == fa) continue ; 
        dfs(v , dep + 1 , u , cnt) ;
        cnt++ ;  
    }
}
signed main(){
//    freopen("test.in" , "r" , stdin) ;
//    freopen("test.out" , "w" , stdout) ;
    n = read() ; k = read() ; 
    for(int i = 1 ; i < n ; i++){
        int u = read() , v = read() ; 
        G[u].push_back(v) ; G[v].push_back(u) ;   
    }
    dfs(1 , 1 , 1 , 0) ; 
    int ans = 1 ; 
    for(int i = 1 ; i <= n ; i++)
        ans = ans * val[i] % 1000000007 ; 
    printf("%lld" , ans) ; 
    return 0 ;
}

M题我写的是树刨加莫队呃呃感觉有点离谱不知道正解是啥好在一次过了

我的最根本想法就是先求两点距离然后两点间有多少个颜色为x的边同时计算这些边为x的边的和用我们求的两点距离减去和加上颜色为x的边数 * y

两点距离很好算直接统计一下到根节点的距离然后减个lca到根节点的距离都行非常简单

所以求这两点之间有多少个颜色为x的边并且还要去算这些颜色为x的边的和才是重头戏

用树刨的思想先把两点之间拆成区间然后把这些询问给离线出来最后再算回去即可

需要注意的是由于这里是边上有值而不是点上

所以我们需要转化一下把边的值下放到层数更低的点

还有一个非常重要的细节就是树链剖分最后一次查询和修改路径的时候，父亲结点是不在路径上的因为父亲结点的点权代表的是它与它的父亲之间的边权，因此，在查询和修改的时候，最后左端点为

#include<bits/stdc++.h>
using namespace std ;
#define maxn 100100
#define int long long
int read(){
    int ans = 0 , f = 1 ; char ch = getchar() ;
    while ( !isdigit(ch) ){ if( ch == '-' ) f = -1 ; ch = getchar() ; }
    while ( isdigit(ch) ) ans = (ans * 10) + (ch ^ '0') , ch = getchar() ;
    return ans * f ;
}
int n , q , len;  
int siz[maxn] , fa[maxn] , son[maxn] , dep[maxn] , top[maxn]  , w[maxn] , cloc ; 
int to[maxn << 1] , nxt[maxn << 1] , head[maxn] , cnt , dis[maxn << 1] , yanse[maxn << 1]; 
inline void addedge(int u , int v , int ddd , int c){
    to[++cnt] = v ; nxt[cnt] = head[u] ; head[u] = cnt; dis[cnt] = ddd ; yanse[cnt] = c ; return ; 
} 
int val[maxn] , valc[maxn] , color[maxn] , colorc[maxn]; 
int qsum[maxn] , cntt[maxn] , sum[maxn]; 
void dfs1(int u , int f , int deep){
    fa[u] = f ; siz[u] = 1 ; dep[u] = deep ; int maxson = 0 ; 
    for(int i = head[u] , v ; i ; i = nxt[i]){
        v = to[i] ; 
        if(v == f) continue ; 
        val[v] = dis[i] ; color[v] = yanse[i] ; 
        dfs1(v , u , deep + 1) ;
        siz[u] += siz[v] ; 
        if(siz[v] > maxson ) maxson = siz[v] , son[u] = v ; 
    } 
}
void dfs2(int u , int tp){
    w[u] = ++cloc ; valc[cloc] = val[u] ; top[u] = tp ; colorc[cloc] = color[u] ; 
    if(son[u])  dfs2(son[u] , tp) ; 
    for(int i = head[u] , v; i ; i = nxt[i]){
        v = to[i] ;
        if(v == fa[u] || v == son[u]) continue ; 
        dfs2(v , v) ; 
    }
}
int belong(int x){
    return ((int)ceil((float)x/len)) ; 
}
struct node{
    int l , r , id , c ; 
    bool operator <(const node& x) const{
        return (belong(l)^belong(x.l))?belong(l)<belong(x.l):((belong(l)&1)?r<x.r:r>x.r);
    }
}que[maxn * 20];
void add(int x){
    cntt[colorc[x]]++ ; 
    sum[colorc[x]] += valc[x] ; 
    return ; 
}
void del(int x){
    cntt[colorc[x]]-- ; 
    sum[colorc[x]] -= valc[x] ; 
    return ; 
}
int anscnt[maxn * 20] , anssum[maxn * 20] , temp ; 
int xx[maxn] , yy[maxn] , uu[maxn] , vv[maxn] ; 
void pre(int u , int v , int x){
    while(top[u] != top[v]){
        if(dep[top[u]] < dep[top[v]]) swap(u , v) ; 
//        ans = max(ans , query(1 , 1, n , w[top[u]] , w[u] )) ;
        que[++temp] = (node){w[top[u]] , w[u] , temp , x} ; 
        u = fa[top[u]] ; 
    }
    if(dep[u] < dep[v]) swap(u , v) ; 
//    ans = max(ans , query(1 , 1, n , w[son[v]] , w[u])) ;
    que[++temp] = (node){w[son[v]] , w[u] , temp , x} ; 
}
signed main(){
//    freopen("test.in" , "r" , stdin) ;
//    freopen("test.out" , "w" , stdout) ;
    n = read() ; q = read() ; len = sqrt(n) ; 
    for(int i = 1 , u , v , ddd , c ; i < n ; i++){
        u = read() , v = read() , c = read() , ddd = read() ; 
        addedge(u , v , ddd ,c ) ; addedge(v , u , ddd , c) ; 
    }
    dfs1(1  , 1 , 1) ; dfs2(1 ,1 ) ; 
    for(int i = 1 ; i <= n ; i++){
        qsum[i] = qsum[i - 1] + valc[i] ; 
    }
    for(int i = 1 ; i <= q ; i++){
        xx[i] = read() , yy[i] = read() , uu[i] = read() , vv[i] = read() ; 
        pre(uu[i] , vv[i] , xx[i]) ; 
    }
    sort(que + 1 , que + 1 + temp) ; 
    int l = 1 , r = 0 ; 
    for(int i = 1 ; i <= temp ; i++){
        int ql = que[i].l , qr = que[i].r ; 
        while(r < qr) add(++r) ; 
        while(r > qr) del(r--) ; 
        while(l < ql) del(l++) ; 
        while(l > ql) add(--l) ; 
        anscnt[que[i].id ] = cntt[que[i].c ] ; 
        anssum[que[i].id ] = sum[que[i].c ] ; 
    }
    temp = 0 ; 
    for(int i = 1 ; i <= q ; i++){
        int ans1 = 0 , ans2 = 0 ; 
        int u = uu[i] , v = vv[i] ; 
        while(top[u] != top[v]){
            if(dep[top[u]] < dep[top[v]]) swap(u , v) ; 
//            ans = max(ans , query(1 , 1, n , w[top[u]] , w[u] )) ;
            ans1 += qsum[w[u]] - qsum[w[top[u]] - 1] ; 
            ++temp ; 
            ans1 -= anssum[temp] ; 
            ans2 += anscnt[temp] ; 
            u = fa[top[u]] ; 
        }
        if(dep[u] < dep[v]) swap(u , v) ; 
//        ans = max(ans , query(1 , 1, n , w[son[v]] , w[u])) ;
        ans1 += qsum[w[u]] - qsum[w[son[v]] - 1] ; 
        ++temp ; 
        ans1 -= anssum[temp] ; 
        ans2 += anscnt[temp] ; 
        ans1 += ans2 * yy[i] ; 
        printf("%lld\n" , ans1) ; 
    }
    return 0 ;
}

posted @ 2023-01-09 22:24 Vellichor_zht 阅读(100) 评论(0) 收藏举报

刷新页面返回顶部

Vellichor

1.9寒假集训-进阶训练赛（五）A-M题解

公告