[$Solution$] [九省联考 $2018$] 一双木棋（$chess$）

[\(Solution\)] [九省联考 \(2018\)] 一双木棋（\(chess\)）

本文所有权属于：FrSmT

题意：

菲菲和牛牛在一块棋盘上下棋，菲菲执黑棋先手，牛牛执白棋后手。

棋局开始时，棋盘上没有任何棋子，两人轮流在格子上落子，直到填满棋盘时结束。

落子的规则是：一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子。

棋盘的每个格子上，都写有两个非负整数

在游戏结束后，菲菲和牛牛会分别计算自己的得分：菲菲的得分是所有有黑棋的格子上数值的和。

菲菲和牛牛都希望，自己的得分减去对方的得分得到的结果最大。现在他们想知道，在给定的棋盘上，如果双方都采用最优策略且知道对方会采用最优策略，那么，最终的结果如何？

状态设计：

由于n，m范围较小，不难想到状压dp，但是显然不可能记录整个棋盘。

有考虑到题目中说到左边和上方都要选，那么不能想到轮廓线\(DP\)。

将横着的棋盘轮廓设为\(0\)，竖着的棋盘轮廓设为\(1\)，用一个十进制整数表示从左下到右上的一条轮廓线

例如对于这张棋盘，用二进制表示则为\(00101\)

接下来以样例为例，解释具体情况：

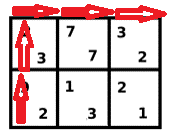
初始情况，棋盘为：\(11000\)，每一次寻找轮廓线中的所有向内凹的拐角（因为只有上左都被选过之后这个点才可以被选），例如在第一行第一列处进行dp，进入下一个状态。

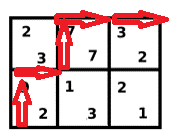
第一步：\(10100\)

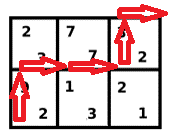
第二步：\(10010\)

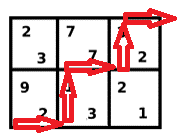
第三步：\(01010\)

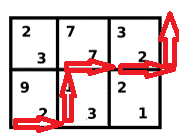
第四步：\(01001\)

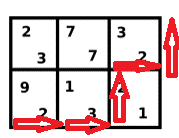
第五步：\(00101\)

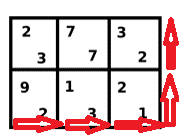
第六步：\(00011\)
\(\\\)
考虑这整个过程，就是一个将\(10\)的二进制数，变成\(01\)

所以状态设计为

\(dp[state]\)表示"当棋盘状态为\(state\)时先手得分与后手得分之差的最大值"。

这样做的好处是不用分情况讨论，不管是莉莉还是牛牛，其实本质上想得到的都是自己的得分减去对方得分的差最大。

状态转移方程：$dp[state]=max(dp[state],w[who][x][y]-dfs(next，who \(^\) 1))$

//\(next\)表示在内拐点处落子后的情况。

边界条件：

if(i==n&&j==m)return dp[state]=0;

AC CODE:

#include<bits/stdc++.h>
#define isnum(ch) ('0' <= ch && ch <= '9')
using namespace std;
int n,m,w[2][11][11];
int dp[1<<(20)];
int dfs(int i,int j,int who,int state)
{
	if(i==n&&j==m)return dp[state]=0;
	if(dp[state])return dp[state];
	int res=-1e9;
	int x=n+1,y=1,tstate;
	for(int k=0;k<n+m-1;k++)
	{
		if((1<<k)&state)x--;//得到现在的棋盘状态
		else y++;
		if(!(((1<<k)&state)>0&&((1<<k+1)&state)==0))continue;
		tstate=state^(3<<k);//得到下一步的棋盘状态
		res=max(res,w[who][x][y]-dfs(x,y,who^1,tstate));//状态转移
	}
	return dp[state]=res;
}
signed main()
{
	cin>>n>>m;
	for(int k=0;k<=1;k++)
	for(int i=1;i<=n;i++)
	for(int j=1;j<=m;j++)
	cin>>w[k][i][j];
	int s=0;
	for(int i=1;i<=n;i++)s^=1<<i-1;
	cout<<dfs(1,1,0,s)<<endl;
	return 0;
}

%%%%Orz