决策树

决策树的定义
决策树（decision tree）：是一种基本的分类与回归方法，此处主要讨论分类的决策树。在分类问题中，表示基于特征对实例进行分类的过程，可以认为是if-then的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。决策树通常有三个步骤：特征选择、决策树的生成、决策树的修剪。
决策树的构造
首先先选择一个最优特征，并根据该特征对训练数据进行分割，使得各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。首先构建根节点，将所有训练数据都放在根节点，选择一个最优特征，按着这一特征将训练数据集分割成子集，使得各个子集有一个在当前条件下最好的分类。如果这些子集已经能够被基本正确分类，那么构建叶节点，并将这些子集分到所对应的叶节点去。如果还有子集不能够被正确的分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的节点，如果递归进行，直至所有训练数据子集被基本正确的分类，或者没有合适的特征为止。每个子集都被分到叶节点上，即都有了明确的类，这样就生成了一颗决策树。
信息增益
划分数据集的大原则是：将无序数据变得更加有序，但是各种方法都有各自的优缺点，信息论是量化处理信息的分支科学，在划分数据集前后信息发生的变化称为信息增益，获得信息增益最高的特征就是最好的选择，所以必须先学习如何计算信息增益，集合信息的度量方式称为香农熵，或者简称熵。信息增益是一个统计量，用来描述一个属性区分数据样本的能力。信息增益越大，那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量。计算公式如下：

最终我们选择信息熵最大的作为根节点，子节点同样。
在现实生活中，男女的体重身高有着明显差异 我们可以通过身高体重去区别男女。
代码实例实现
1.计算香农熵
def calcShannonEnt(dataSet):

numEntries=len(dataSet)

labelCounts={}

for featVec in dataSet:
    currentLabel=featVec[-1]                   
    if currentLabel not in labelCounts.keys():   
        labelCounts[currentLabel]=0
    labelCounts[currentLabel]+=1                

shannonEnt=0.0                                  

for key in labelCounts:
    prob=float(labelCounts[key])/numEntries    
    shannonEnt-=prob*log(prob,2)                
return shannonEnt                                

2.构造数据集
def createDataSet():

dataSet=[[0, 0, 'woman'],
        [1, 0, 'woman'],
        [1, 1, 'man'],
        [1, 1, 'man'],
        [0, 0, 'woman'],
        [0, 1, 'woman'],
        [1, 0, 'woman'],
        [1, 1, 'man']]
   

labels=['身高','体重']
#身高1代表高 体重1代表重 

return dataSet,labels

3.按照给定特征划分数据集
def splitDataSet(dataSet,axis,value):
retDataSet=[]
for featVec in dataSet:
if featVec[axis]==value:
reduceFeatVec=featVec[:axis]
reduceFeatVec.extend(featVec[axis+1:])
retDataSet.append(reduceFeatVec)
return retDataSet
4.计算给定数据集的香农熵
def chooseBestFeatureToSplit(dataSet):

numFeatures = len(dataSet[0]) - 1

baseEntropy = calcShannonEnt(dataSet)

bestInfoGain = 0.0

bestFeature = -1

for i in range(numFeatures):

    featList = [example[i] for example in dataSet]
 
    uniqueVals = set(featList)
  
    newEntropy = 0.0
   
    for value in uniqueVals:
       
        subDataSet = splitDataSet(dataSet, i, value)
       
        prob = len(subDataSet) / float(len(dataSet))
       
        newEntropy += prob * calcShannonEnt((subDataSet))
   
    infoGain = baseEntropy - newEntropy
  
   
  
    if (infoGain > bestInfoGain):
       
        bestInfoGain = infoGain
       
        bestFeature = i
        
return bestFeature

5.统计classList中出现次数最多的元素
def majorityCnt(classList):
classCount={}

for vote in classList:
    if vote not in classCount.keys():
        classCount[vote]=0
        classCount[vote]+=1
   
    sortedClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

6. 创建决策树
   def createTree(dataSet,labels,featLabels):

   classList=[example[-1] for example in dataSet]

   if classList.count(classList[0])len(classList):
   return classList[0]
   if len(dataSet[0])1:
   return majorityCnt(classList)

   bestFeat=chooseBestFeatureToSplit(dataSet)

   bestFeatLabel=labels[bestFeat]
   featLabels.append(bestFeatLabel)

   myTree={bestFeatLabel:{}}

   del(labels[bestFeat])

   featValues=[example[bestFeat] for example in dataSet]

   uniqueVls=set(featValues)

   for value in uniqueVls:
   myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet,bestFeat,value),
   labels,featLabels)
   return myTree
   7.获取决策树叶子节点的数目
   def getNumLeafs(myTree):
   numLeafs=0
   firstStr=next(iter(myTree))
   secondDict=myTree[firstStr]
   for key in secondDict.keys():
   if type(secondDict[key]).name'dict':
   numLeafs+=getNumLeafs(secondDict[key])
   else: numLeafs+=1
   return numLeafs
   8.获取决策树的层数
   def getTreeDepth(myTree):
   maxDepth = 0
   firstStr = next(iter(myTree))
   secondDict = myTree[firstStr]
   for key in secondDict.keys():
   if type(secondDict[key]).name'dict':
   thisDepth = 1 + getTreeDepth(secondDict[key])
   else: thisDepth = 1
   if thisDepth > maxDepth: maxDepth = thisDepth
   return maxDepth
   9.绘制结点
   def plotNode(nodeTxt, centerPt, parentPt, nodeType):
   arrow_args = dict(arrowstyle="<-")
   font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
   createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
   xytext=centerPt, textcoords='axes fraction',
   va="center", ha="center", bbox=nodeType, arrowprops=arrow_args, fontproperties=font)
   def plotMidText(cntrPt, parentPt, txtString):
   xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
   yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
   createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
   10.绘制决策树
   def plotTree(myTree, parentPt, nodeTxt):
   decisionNode = dict(boxstyle="sawtooth", fc="0.8")
   leafNode = dict(boxstyle="round4", fc="0.8")
   numLeafs = getNumLeafs(myTree)
   depth = getTreeDepth(myTree)
   firstStr = next(iter(myTree))
   cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
   plotMidText(cntrPt, parentPt, nodeTxt)
   plotNode(firstStr, cntrPt, parentPt, decisionNode)
   secondDict = myTree[firstStr]
   plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
   for key in secondDict.keys():
   if type(secondDict[key]).name=='dict':
   plotTree(secondDict[key],cntrPt,str(key))
   else:
   plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
   plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
   plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
   plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
   11.创建绘制面板与输出
   def createPlot(inTree):
   fig = plt.figure(1, facecolor='white')#创建fig
   fig.clf()#清空fig
   axprops = dict(xticks=[], yticks=[])
   createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)#去掉x、y轴
   plotTree.totalW = float(getNumLeafs(inTree))#获取决策树叶结点数目
   plotTree.totalD = float(getTreeDepth(inTree))#获取决策树层数
   plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0#x偏移
   plotTree(inTree, (0.5,1.0), '')#绘制决策树
   plt.show()#显示绘制结果

if name == 'main':
dataSet, labels = createDataSet()
featLabels = []
myTree = createTree(dataSet, labels, featLabels)
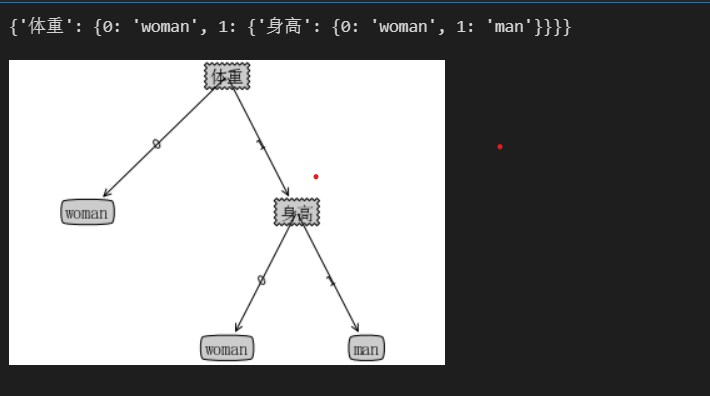
print(myTree)
createPlot(myTree)

if name=='main':
dataSet,labels=createDataSet()
featLabels=[]
myTree=createTree(dataSet,labels,featLabels)
print(myTree)