实验4

实验任务1：

思考回答：

不可以，因为一元二次方程一般有两个解，但是调用函数只能返回一个值。

实验任务2：

#include <stdio.h>
long long fac(int n);

int main()
{
  int i,n;
  printf("Enter n: ");
  scanf("%d",&n);

  for(i=1;i<=n;i++)
  {
    printf("%d!=%lld\n",i,fac(i));
  }
  return 0;

}

long long fac(int n)
{
  static long long p = 1;


  p = p*n;

  return p;
}

 

 

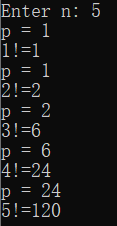
#include <stdio.h>
int func(int,int);

int main()
{
  int k=4,m=1,p1,p2;
  p1 = func(k,m);
  p2 = func(k,m);
  printf("%d,%d\n",p1,p2);

  return 0;
}

int func(int a,int b)
{
  static int m=0,i=2;

  i+=m+1;
  m=i+a+b;

  return (m);
}

理论分析与结果一致。

局部static变量特性：当此变量有一个值后，不会再为此变量赋初始值。

实验任务3：

#include <stdio.h>

#define N 1000
int fun(int n,int m,int bb[N]) {
    int i,j,k=0,flag;
    
    for(j=n;j<=m;j++) {
        flag = 1;   
        for(i=2;i<j;i++)
            if(j%i==0) {  
               flag=0;
               break;
        }
        if(flag == 1) 
           bb[k++]=j;
    }
    return k;
}

int main(){
    int n=0,m=0,i,k,bb[N];
    
    scanf("%d",&n);
    scanf("%d",&m);
    
    for(i=0;i<m-n;i++)
        bb[i]=0;
        
    k=fun(n,m,bb); 
    
    for(i=0;i<k;i++)
        printf("%4d",bb[i]);
        
    return 0;
}

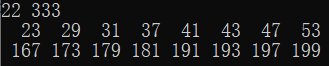
 实验任务4：

#include <stdio.h>
long long fun(int n);

int main() {
    int n;
    long long f;

    while(scanf("%d", &n) != EOF) {
        f = fun(n);
        printf("n = %d, f = %lld\n", n, f);
    }

    return 0;
}

long long fun(int n)
{
    long long s;
    if (n==1)
    return n;
    else
    s=fun(n-1)*2+1;
    return s;
}

 

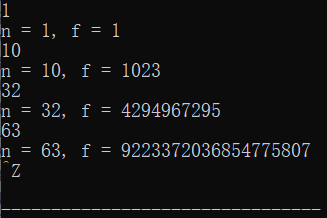
 实验任务5：

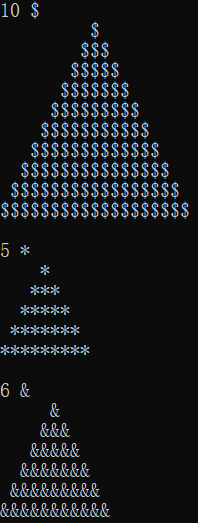
#include <stdio.h>

void draw(int n, char symbol);  // 函数声明 

#include <stdio.h> 
int main() {
    int n, symbol;
    
    while(scanf("%d %c", &n, &symbol) != EOF) {
        draw(n, symbol);  // 函数调用 
        
        printf("\n");
    }
    
    return 0;
} 


// 函数定义
// 补足代码。。。 

void draw(int n,char symbol)
{
    int i,j,q,r;
    r=n;
    for(i=1;i<=n;i++)
    {
        
        for(j=1;j<r;j++)
        {
            printf(" ");
        }
        for(q=1;q<i;q++)
        {
            printf("%c",symbol);
        }
        for(q=1;q<i;q++)
        {
            printf("%c",symbol);
        }
        printf("%c\n",symbol);
        r--;
    }
}