【题解】CF773D Perishable Roads
Statement
给定一个 \(n\) 点的无向完全图，有边权。对于每个 \(i\in [1,n]\) ，求以 \(i\) 为根节点的生成树中，最小的 \(\sum d(x)\) 是多少。
定义 \(d(x)\) ：\(x\) 到根节点所有边中权值最小的一条
Solution
不愧是 tourist （这场比赛里）最喜欢的题啊……
由于代价是取 \(\min\) 的，考虑找最小的边权。如果这条边已经被连到了根，那么剩下的点直接连向这个点即可（完全图）。
设最小的边为 \(edmn\) ，易知最优解（或之一）的上面部分一定是一条根到 \(edmn\) 两个端点之一的链。
由于这个东西是个完全图，而且代价是取 \(\min\) 的，所以其实链下面的部分是树是链完全没有关系（因为代价已经被 \(edmn\) 给确定了），形态不重要。下面直接将最优解所选择的边当成链来处理。
那么把所有边权减去 \(edmn\) ，最后再加上 \((n-1)\times edmn\) ，不影响答案。
现在设这个最优解的路径为 \(w_1,\dots,w_{n-1}\) .令 \(k\) 为路径上标号最小的、边权为 0 的边（ 也就是最小的 \(k\) 满足 \(w_k=0\) ）
有结论： 对于所有的 \(i\leq k-3\) ，有 \(w_i>w_{i+1}\)
Proof
（看了半天才懂……）
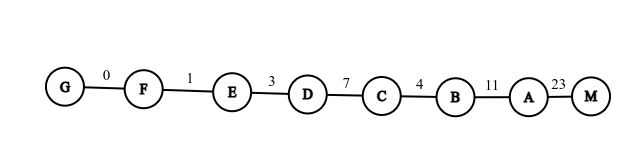
假设现在有这样一条路径，\(M\) 是根节点，\(G\) 是令 \(w_k=0\) 的节点。
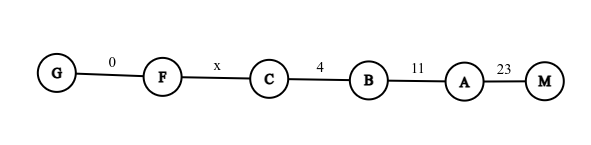
此处 \(w_{CD}\) 不满足上面的性质。那么可以将其替换如下：
\(x\) 是新的边权。设原来 \(M\sim C\) 的最小值为 \(t\) ，那么减少贡献为：
\[\delta =calc(D)+calc(E)=\min(w_{CD},t)+\min(w_{DE},w_{CD},t)\\ \because w_{CD}>t,w_{DE}<w_{CD}\\ \therefore \min{(w_{CD},t)}=t,\min(w_{DE},w_{CD},t)=\min(w_{DE},t)\\ \delta=t+\min(w_{DE},t) \]增加的贡献是：
\[\Delta =calc(F')-calc(F)=\min(w_{CF},t)-w_{DE}<t<t+\min(w_{DE},t) \]那么就有：
\[\delta>\Delta \]所以这样替换过后，贡献一定会减少，就不符合最优解的前提了。
Q.E.D.
有了这个结论事情就简单多了。除了最后两条边，其他边的贡献（由于递增）就是边权，可以建一个超级源点 \(S\) ，对于所有 0 边的端点连 0 边权的边，（当然要加上原图中的所有边）直接跑最短路。
现在来讨论 \(k-2\leq i\leq k-1\) 的情况。
- \(w_{k-2}>w_{k-1}\) 。那么情况就等同于整条路径符合上面的结论，直接按原先的边权跑最短路即可，无需特殊处理。
- \(w_{k-2}\leq w_{k-1}\) 。设当前的路径是这样的：
A---(k-2)----B----(k-1)----C---0----，那么显然，这样的路径中，我们先走到 \(A\) ，然后通过两条路径走到 0 边的一个端点 \(C\) ，（根据前面的结论，\(w_i\) 显然都比 \(w_{k-2}\) 大，所以不用考虑）代价是 \(2\times w_{k-2}\) .那么就在之前的基础上再加上一条 \(S,i\) 之间，\(\min\{dis[i][j]\times 2\}\) 的边即可（注意，需要满足 \(i\neq j\) 且 \(i,j\) 均不是 0 边端点，相当于在枚举 \(w_{k-2}\) ）。
那么这样就做完了。
妙啊。不愧是 tourist 。
顺便一说，Dijkstra 就直接朴素的好了，反正之前的操作已经 \(\mathcal{O}(n^2)\) 了
Code
//Author: RingweEH
const ll inf=1e16;
const int N=2010;
struct edge
{
int to,nxt; ll val;
}e[N*N<<1];
int tot=0,head[N],n,S;
bool tag[N],vis[N];
ll mp[N][N],dis[N],mn[N];
void add( int u,int v,ll w )
{
e[++tot].to=v; e[tot].val=w; e[tot].nxt=head[u]; head[u]=tot;
}
int main()
{
n=read(); S=n+1; ll edmn=inf;
for ( int i=1; i<n; i++ )
for ( int j=i+1; j<=n; j++ )
mp[j][i]=mp[i][j]=read(),edmn=min( edmn,mp[i][j] );
for ( int i=1; i<=n; i++ )
for ( int j=1; j<=n; j++ )
if ( i^j )
{
mp[i][j]-=edmn; add( i,j,mp[i][j] );
if ( !mp[i][j] ) tag[i]=1,add( S,i,0 );
}
memset( mn,0x7f,sizeof(mn) );
for ( int i=1; i<=n; i++ )
for ( int j=1; j<=n; j++ )
if ( (!tag[i]) && (!tag[j]) && (i^j) ) mn[i]=min( mn[i],mp[i][j]*2ll );
for ( int i=1; i<=n; i++ )
add( S,i,mn[i] );
memset( dis,0x3f,sizeof(dis) ); dis[S]=0;
for ( int j=1; j<=n; j++ )
{
ll mnval=inf; int mnpos=0;
for ( int i=1; i<=n+1; i++ )
if ( !vis[i] && dis[i]<mnval ) mnval=dis[i],mnpos=i;
vis[mnpos]=1;
for ( int i=head[mnpos]; i; i=e[i].nxt )
dis[e[i].to]=min( dis[e[i].to],dis[mnpos]+e[i].val );
}
ll addval=(n-1)*edmn;
for ( int i=1; i<=n; i++ )
printf( "%lld\n",dis[i]+addval );
return 0;
}
