训练指南第三章x第五章 刷题记录
注:前面有一些题目直接跳过了,第五章当时是没做完的
粘贴的时候出过一些bug……希望没有少东西
3.1 基础数据结构
并查集
思路:把每种元素作为点,每次放入的时候如果在同一个集合里说明形成了环,就 refuse 掉.
思路:并查集维护父亲,路径压缩的时候维护到父亲的距离即可.注意更新距离.
3.2 区间信息维护与查询
3.2.1 树状数组
思路:题目的意思就是两个人的比赛裁判员能力在两人中间,且房子一定要在他们中间.设 \(a_1\sim a_{i-1}\) 中有 \(c_i\) 个比 \(a_i\) 小,\(a_{i+1}\sim a_n\) 中有 \(d_i\) 个比 \(a_i\) 大,那么对于一个人 \(i\) ,以他为裁判的比赛数就是 \(c_i\times d_i+(i-1-c_i)\times (n-i-d_i)\) ,那么问题就在于如何求 \(c_i,d_i\) .
考虑树状数组求逆序对的思路.同理,这里的 \(a_i\leq 1e5\) ,那么可以从前到后扫一遍,每次 \(tr[a_j]++\) ,统计 \(a_i\) 的时候就统计 \(1\sim a_i\) 的前缀和即可.倒序再做一遍.
Code
void add( int x,int val ) { for ( ; x<=N-10; x+=lowbit(x) ) tr[x]+=val; }
//注意这里的值域不是n...调了半天
ll query( int x )
{
ll res=0;
for ( ; x; x-=lowbit(x) ) res+=tr[x];
return res;
}
for ( int i=1; i<=n; i++ )
c[i]=query(a[i]),add( a[i],1 );
memset( tr,0,sizeof(tr) );
for ( int i=n; i>=1; i-- )
d[i]=query(a[i]),add(a[i],1);
ll ans=0;
for ( int i=1; i<=n; i++ )
ans=ans+c[i]*(n-i-d[i])+(i-1-c[i])*d[i];
3.2.2 RMQ问题
用倍增的思想计算区间最小值.
令 \(d[i][j]\) 表示从 \(i\) 开始,长度为 \(2^j\) 的一段元素中的最值,和 LCA 一样的思想,有 \(d[i][j]=min(d[i][j-1],d[i+2^{j-1}][j-1])\) ,\([L,R]\) 区间的答案即为 \(min(d[L][k],d[R-(1<<k+1)][k])\)
\(2^k\leq R-L+1<2^{k+1}\)
思路: 第一反应是排序,但是题目中说了 in non-decreasing order 所以根本没这个必要.那么首先把所有重复数字转化成二元组的形式,即(数字,出现次数).然后就是对出现次数序列进行 RMQ ,然后输出对应的数字即可.
Code
void ST_init() {}
int query( int l,int r )
{
if ( a[l]==a[r] ) return r-l+1;
int res=-1000010,k=0;
res=max( res,max(R[l]-l+1,r-L[r]+1 ) );
l=R[l]+1; r=L[r]-1;
if ( l>r ) return res;
while ( (1<<(k+1))<=r-l+1 ) k++;
return max( res,max( st[l][k],st[r-(1<<k)+1][k] ) );
}
int main()
{
while ( scanf( "%d",&n ) && n )
{
//Clear && readin
int cntk=0,rk=n,rnk=0,k=0;
for ( int i=1; i<=n+1; i++ )
{
if ( a[i]!=a[i-1] )
{
int j=i-1;
while ( j && !cnt[j] ) cnt[j--]=cntk;
cntk=0;
}
cntk++;
}
ST_init();
for ( int i=1; i<=n; i++ )
{
if ( a[i]!=a[i-1] ) k=i;
L[i]=k; int tmp=n-i+1;
if ( a[tmp]!=a[tmp+1] ) rk=tmp;
R[tmp]=rk;
}
int l,r;
while ( q-- )
{
scanf( "%d%d",&l,&r );
if ( a[l]==a[r] ) printf( "%d\n",r-l+1 );
else printf( "%d\n",query( l,r ) );
}
}
return 0;
}
3.2.3 线段树:点修改
UVA1400 "Ray, Pass me the dishes!"
思路:要求一个动态区间的最大连续和,那么考虑这个和是由哪些部分组成的,构造一棵线段树,每个节点记录,前缀最大值,后缀最大值,和整个区间里的最大连续子段和.
Attention:不能在有返回值的函数里面不 return ,可能会产生 RE 等奇怪错误
Code
struct Segment
{
int l,r; ll val;
Segment ( int _l=0,int _r=0,ll _val=0 ) { reset(_l,_r,_val); }
void reset( int _l,int _r,ll _val ) { l=_l,r=_r,val=_val; }
Segment operator + ( const Segment &tmp )
{
return Segment( min(l,tmp.l),max( r,tmp.r),val+tmp.val );
}
bool operator < ( const Segment &tmp ) const
{
if ( val^tmp.val ) return val<tmp.val;
if ( l^tmp.l ) return l>tmp.l;
return r>tmp.r;
}
};
struct SegTree{ int l,r; Segment sub,pre,suf; }tr[N<<2];
SegTree pushup ( SegTree t1,SegTree t2 ) {}
void build( int rt,int l,int r ) {}
SegTree query( int rt,int l,int r )
{
if ( l<=tr[rt].l && r>=tr[rt].r ) return tr[rt];
int mid=(tr[rt].l+tr[rt].r)>>1;
if ( l<=mid && r>mid ) return pushup( query(lson(rt),l,r),query(rson(rt),l,r) );
else if ( r<=mid ) return query( lson(rt),l,r );
else return query( rson(rt),l,r );
}
3.2.4 线段树:区间修改
区间加的话打个 tag 然后累加就好了。如果是区间修改那么还要标记下传。
UVA11992 Fast Matrix Operations
思路:题意是在矩阵中支持三种操作:子矩阵区间加,区间修改,区间求和。相当于是一个线段树的二维区间维护问题。那么给每一行建一棵线段树,然后照常维护即可。
但是听上去很麻烦……有没有更简单的方法? 当然是把数组展开成一行了
线段树虽然码量大但确实很常用……写多了还能增加码力 (bushi)
把 tagadd 清零成 -1 的我宛如一个zz……
Code
value get_value( value a,value b )
{
return value( a.sum+b.sum,max(a.max,b.max),min(a.min,b.min) );
}
void add_tree( int u,int val )
{
tr[u].tagadd+=val; tr[u].val.sum+=(tr[u].r-tr[u].l+1)*val;
tr[u].val.max+=val; tr[u].val.min+=val;
}
void set_tree( int u,int val )
{
tr[u].tagadd=0; tr[u].tagset=val;
tr[u].val.sum=(tr[u].r-tr[u].l+1)*val;
tr[u].val.min=val; tr[u].val.max=val;
}
void pushup( int u ){}
void pushdown( int u ) { }
void build( int u,int l,int r ) { }
void add_Seg( int u,int l,int r,int val ) {}
void set_Seg( int u,int l,int r,int val ) {}
value query( int u,int l,int r )
{
if ( l<=tr[u].l && tr[u].r<=r ) return tr[u].val;
pushdown( u );
value res; res.reset( 0,-inf,inf );
int mid=(tr[u].l+tr[u].r)>>1;
if ( l<=mid ) res=get_value( res,query(lson(u),l,r) );
if ( r>mid ) res=get_value( res,query( rson(u),l,r ) );
return res;
}
3.5 排序二叉树
3.5.1 基本概念
性质:满足所有左子树的节点都比根节点小,右子树反之。
最常见的操作是旋转维护平衡。比如:
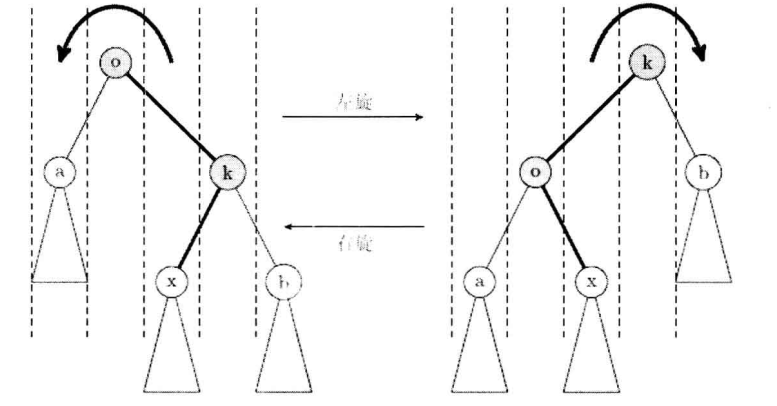
陈峰/刘汝佳:本着不要重新发明轮子的作风,如果 set,map 已经可以满足要求,建议不要实现自己的平衡 BST 这就是工程党的作风吗,爱不起来
思路:显然,所有被保留的点均在上一个点的下方且在右方(不然易证会有一个点被 pop 掉) ,用 multiset 表示这个点集。如果这个点不会被放入,那么比较 lower_bound(P) 和 P.y ;如果要用这个点去删点,那么从 upper_bound(P) 开始删除即可。
Code
struct node
{
int x,y;
bool operator < ( const node &tmp ) const
{
return x<tmp.x || ( x==tmp.x && y<tmp.y );
}
};
multiset<node> S;
multiset<node> :: iterator it;
while ( n-- )
{
int x,y; scanf( "%d%d",&x,&y );
node p=(node){x,y}; it=S.lower_bound(p);
if ( it==S.begin() || (--it)->y>y )
{
S.insert(p); it=S.upper_bound(p);
while ( it!=S.end() && it->y>=y ) S.erase( it++ );
}
printf( "%lu\n",S.size() );
}
3.5.2 用 Treap 实现名次树
其实就是平衡树的 kth 和 get_rank .
思路:支持删边,查询第 \(k\) 大的点权,修改点权,而且可以离线。那么就可以把操作倒序,那么就可以把删边换成加边。然后点权修改就改成插入和删除。加边的时候维护一个并查集,如果两个在同一个里面就没有影响,否则合并两棵平衡树。稍微优化的话就是把 size 小的树合并到大的里面即可。
Code
struct Treap
{
int val[N],rnd[N],siz[N],son[2][N],num[N];
void pushup( int u ) { }
int new_node( int v ) {}
int merge( int x,int y ) {}
void split( int u,int k,int &x,int &y ) {}
int kth( int u,int k ) {}
void insert( int &u,int v ) { }
void Delete( int &u,int v ){ }
}tr;
int find( int x )
{
return fa[x]==x ? x : fa[x]=find(fa[x]);
}
void bing( int u,int v )
{
if ( tr.siz[rt[u]]<tr.siz[rt[v]] ) swap( u,v );
while ( tr.siz[rt[v]] )
{
int now=tr.kth( rt[v],1 );
tr.insert( rt[u],tr.val[now] ); tr.Delete( rt[v],tr.val[now] );
}
fa[v]=u; rt[v]=0;
}
3.5.3 用伸展树实现可分裂与合并的序列
刚用 FHQ 写过去的我看着 “实现可分裂合并”宛如zz
UVA11922 Permutation Transformer
思路:???文艺平衡树模板题???害怕。哦,不太一样,翻转之后还要添加到尾部呢qwq 这有区别吗
Code
struct FHQTreap
{
int l,r,val,rnd,siz,mark;
}tr[N];
int n,cnt=0,rt=0,m;
void update( int x ) { tr[x].siz=tr[tr[x].l].siz+tr[tr[x].r].siz+1; }
int new_node( int val ) {}
void pushdown( int x ) { }
void split( int now,int k,int &x,int &y ) {}
int merge( int x,int y ) { }
void dfs( int x )
{
if ( !x ) return; pushdown( x );
dfs( tr[x].l );
printf( "%d\n",tr[x].val );
dfs( tr[x].r );
}
void reverse( int l,int r )
{
int t1,t2,t3,t4;
split( rt,r,t1,t2 ); split( t1,l-1,t3,t4 );
tr[t4].mark^=1; //rt=merge( merge(t3,t4),t2 );
rt=merge( merge( t3,t2 ),t4 );
}
思路:前三个操作,根据之前的铺垫,就是显然的文艺平衡树+插入删除而已。但是最后一个 LCP 比较难搞,显然不能再在上面套一个后缀数组了……不现实啊。所以只能暴力出奇迹,直接记录 Hash ,并在找 LCP 的时候暴力二分猜长度即可。(陈峰:效率和SA也就差了两三倍,所以没问题!)不过考虑到这里还要翻转区间……所以还得多存一个翻转后区间的 Hash 值,不然翻转的效率会被拉垮,反正预处理多一遍效率也是一样的。
Code
int new_node( int x ) {}
void pushup( int x )
{
siz[x]=siz[l(x)]+siz[r(x)]+1;
has[x]=has[l(x)]*powe[siz[r(x)]+1]+val[x]*powe[siz[r(x)]]+has[r(x)];
rehash[x]=rehash[r(x)]*powe[siz[l(x)]+1]+val[x]*powe[siz[l(x)]]+rehash[l(x)];
}
void reverse( int x ) { }
void pushdown( int x ) { }
void split( int x,int k,int &u,int &v ) { }
void merge( int &x,int u,int v )
{
if ( !u || !v ) { x=u|v; return; }
if ( rand()%(siz[u]+siz[v])<siz[u] ) pushdown( u ),x=u,merge( r(x),r(u),v );
else pushdown( v ),x=v,merge( l(x),u,l(v) );
pushup( x );
}
void insert( int &x,int pos,int val ) { }
void Delete( int &x,int pos ) { }
void reverse( int &x,int l,int r ) { }
ull get_hash( int &x,int l,int r )
{
int t1,t2,t3; split( x,r,t1,t2 ); split( t1,l-1,t1,t3 );
ull res=has[t3]; merge( t1,t1,t3 ); merge( x,t1,t2 ); return res;
}
int get_LCP( int &x,int l,int r )
{
int l1=0,r1=n-r+1,res,mid;
while ( l1<=r1 )
{
mid=(l1+r1)>>1;
if ( get_hash(x,l,l+mid-1)==get_hash(x,r,r+mid-1) ) res=mid,l1=mid+1;
else r1=mid-1;
}
return res;
}
void build( int &x,int l=1,int r=n ) {}
3.6 小结与习题
基础数据结构
Broken Keyboard (a.k.a. Beiju Text)
思路:我居然不知道 Home 和 End 是干嘛的……惭愧。\(1e5\) 的数据范围只要模拟就好了吧,可以用链表,不过感觉双端队列会好写一点。哦,不对,双端队列的话头那里会反过来,得再套个栈。
update:因为没考虑到两次 [ 的情况 Wrong Answer 了一发……我好屑/kk
Code
for ( int i=0; i<len; i++ )
{
if ( s[i]=='[' )
{
if ( !sta.empty() )
{
while ( !sta.empty() ) q.push_front(sta.top()),sta.pop();
}
mark=0; continue;
}
if ( s[i]==']' )
{
if ( !sta.empty() )
{
while ( !sta.empty() ) q.push_front(sta.top()),sta.pop();
}
mark=1; continue;
}
if ( mark ) q.push_back( s[i] );
else sta.push( s[i] );
}
if ( !sta.empty() )
{
while ( !sta.empty() ) q.push_front( sta.top() ),sta.pop();
}
while ( !q.empty() ) printf( "%c",q.front() ),q.pop_front();
printf( "\n" );
思路:大根堆和小根堆……?不过倒是很方便,不需要再插入了。虽然不能同时删除,但是显然可以打删除标记。那么就做完了。但是好像用 set 会更好写。
Code
for ( int i=0; i<n; i++ )
{
scanf( "%d",&m );
for ( int j=0,x; j<m; j++ )
scanf( "%d",&x ),ms.insert( x );
int l=*ms.begin(),r=*(--ms.end());
res+=r-l; ms.erase( --ms.end() ); ms.erase( ms.begin() );
}
思路:很显然的并查集。设 \(f[x]\) 表示父节点, \(d[x]\) 表示 \(x\) 与父节点的异或值,对于给出权值的节点,将父节点设为0. (这样在合并的时候需要注意。)查询时,如果存在联通集合的个数为奇数(不能被异或抵消),且根节点不是0,那么就不能确定;否则取所有节点和父节点的异或和即可。
Code
int find( int x ) {}
void query()
{
int k,res=0,num[M],vis[M];
memset( vis,0,sizeof(vis) );
scanf( "%d",&k );
for ( int i=0; i<k; i++ )
scanf( "%d",&num[i] ),num[i]++;
if ( fl ) return;
for ( int i=0; i<k; i++ )
{
int rt=find( num[i] ),cnt=1;
if ( rt==0 || vis[i] ) continue;
for ( int j=i+1; j<k; j++ )
if ( find(num[j])==rt ) cnt++,vis[j]=1;
if ( cnt&1 ) { printf( "I don't know.\n" ); return; }
}
for ( int i=0; i<k; i++ )
res^=dis[num[i]];
printf( "%d\n",res );
}
bool connect()
{
string s; getline( cin,s );
int u,v,w,opt=sscanf( s.c_str(),"%d%d%d",&u,&v,&w );
u++;
if ( opt==2 ) { w=v,v=0; }
else v++;
int fu=find( u ),fv=find( v );
if ( fu==0 ) swap( fu,fv );
if ( fu!=fv ) fa[fu]=fv,dis[fu]=dis[u]^dis[v]^w;
else return (dis[u]^dis[v])!=w;
return 0;
}
思路:合并集合,基操;集合元素个数,基操;移动元素……??这是啥。首先忽略一个 find 就能判掉。但是删点……真的很难搞,因为下面可能还挂着一大串,基本就 TLE 了。
但是考虑一件事情:这些点到了另一个集合之后,显然是不会成为 “根” 的。那么如果我们要移动节点,不妨在最开始对每个节点建立一个虚点作为 “根” ,这样每个实点都不会是代表节点,就能移动了。
话说训练指南好恶心啊……输出格式都是错的/kel
Code
if ( opt==1 )
{
int u,v; scanf( "%d%d",&u,&v );
u=find(u); v=find(v);
if ( u==v ) continue;
ans[v]+=ans[u]; res[v]+=res[u]; fa[u]=v;
}
else if ( opt==2 )
{
int u,v; scanf( "%d%d",&u,&v );
int fu=find( u ),fv=find( v );
ans[fu]--; ans[fv]++;
res[fu]-=u; res[fv]+=u;
fa[u]=fv;
}
else
{
int u; scanf( "%d",&u );
u=find( u );
printf( "%d %lld\n",ans[u],res[u] );
}
区间信息维护
思路:题面讲了半天电阻器(大雾) 单点修改区间求和……树状数组板子。但是……
Input Data is pretty big (∼ 8 MB) so use faster IO. 树状数组/no fast IO/right
卡输出格式和换行个数就nm离谱……
思路:线段树暴力修改……我服了……就这……
不过为啥全都是 fast IO 的 Warning 啊……难不成刷这本书的还有 !ACMer && !OIer 的会用 iostream(
思路:看成扫描线祭……线段树改版。在更新的时候,如果待更新的覆盖了当前的,那么分三种讨论:
- 没赋值过,那么赋值并更新;
- 赋值过但是没有下传,那么如果比没下传的那个标记大就赋值更新;
- 已经下传了,那么递归。
Code
void pushup( int x,int L,int R ) {}
void pushdown( int x ) {}
void modify( int x,int L,int R,int ql,int qr,int val )
{
if ( val<tr[x].minn ) return;
if ( ql<=L && qr>=R )
{
if ( val>=tr[x].maxx )
{
tr[x].tag=tr[x].maxx=tr[x].minn=val;
ans+=R-L+1; return;
}
if ( L==R ) return;
}
pushdown( x );
int mid=(L+R)>>1,lc=x<<1,rc=x<<1|1;
if ( ql<=mid ) modify( lc,L,mid,ql,qr,val );
else pushup( lc,L,mid );
if ( qr>mid ) modify( rc,mid+1,R,ql,qr,val );
else pushup( rc,mid+1,R );
pushup( x,L,R );
}
思路:看题面,反手就是一个康托展开,太显然了。但是要找 “没出现过的数中第k小” ,那么再来一个权值线段树就好了。
思路:看题面和图都有一种计算几何的味道2333 一个很基础的想法就是,首先并查集维护连通块,然后对于每个块记录最上端和最下端(因为是直线,所以只要存在就能过去),如果加入的那个点更新了这个边界,那么在新增的范围内线段树区间加(直接加显然会产生重复之类的问题)。但是还有个问题……合并的时候两个块的贡献重叠部分只能算一个块了,所以还得区间减……?貌似就好了吧。手模一下。应该没问题。
Code
struct SegmentTree
{
struct Tr_node { int l,r,cnt,siz; }tr[N<<2];
struct state { int cnt,siz; }sta;
void clear( int pos,int l,int r ) {}
void build( int pos,int l,int r ) {}
void pushdown( int pos ) { }
void insert( int pos,int l,int r,int x,int val ) { }
state query( int pos,int x ) {}
}ST;
int find( int x ) {}
void merge( int u,int v )
{
fa[u]=v; siz[v]+=siz[u];
limup[v]=max( limup[v],limup[u] ); limdown[v]=min( limdown[v],limdown[u] );
}
排序二叉树(BST)
插曲
我现在才知道,
LA不是UVALive(Vjudge 显示名称),而是ICPC Live Archive……之前一直觉得LA交不上去和UVA很有关系(
思路:一开始以为是一组数据能构建出多少树……又看错题了。题意是让你求有多少个 \(1\sim n\) 的排列能得到一个和给定排列一样的排序二叉树。显然,在给定了 “标准” 排列之后,左右子树有哪些节点已经确定,而先后的插入顺序并没有影响,所以可以随便选,也就是在 (左右节点总数)中选出 (左子树节点数个位置)的方案数,组合数算一下就好了。当然,对于子树内部,要把每个点的左子树方案数同样地算一遍,并乘法原理。由于 \(n\leq 20\) ,所以显然预处理组合数会更加高效。
Code
void init_C(){}
void insert( int pos,int id,int val )
{
if ( tr[pos].key==0 ) { tr[pos].key=val; tr[pos].siz=1; return; }
if ( tr[pos].key<val )
{
if ( !tr[pos].rc ) tr[pos].rc=id;
insert( tr[pos].rc,id,val );
}
else
{
if ( !tr[pos].lc ) tr[pos].lc=id;
insert( tr[pos].lc,id,val );
}
//update lsz,rsz,siz
}
//--------------------------------
ll ans=1;
for ( int i=1; i<=n; i++ )
ans=(ans*C[tr[i].siz-1][tr[i].lsz])%mod;
思路:题意混乱,废话连篇 定义三元组 \((x,y,z),x,y,z\in [1,m]\) ,称三元组 \(A>B\) 当且仅当 \(A\) 有至少一项比 \(B\) 大(单向)。问存在多少三元组比给定的三元组集合中任何一个都大。所以……可以求个补集?毕竟 “只要有一维大” 这个不好维护。然后呢?考虑降维 打击 ,\(m\) 是 \(1e5\) 的,那么枚举 \(z\) 坐标,在每一“层”的二维平面上求补集就好了。
Code
ll calc( node t1 )
{
node t2=*--s.lower_bound(t1),t3=*s.upper_bound(t1);
return 1ll*(t1.y-t3.y)*(t1.x-t2.x);
}
void insert( const node &t1 )
{
it=s.lower_bound(t1);
if ( it==s.end() || it->y<=t1.y )
{
it=--s.upper_bound( t1 );
for ( ; it!=s.end() && it->y<=t1.y; )
rest-=calc( *it ),s.erase( it-- );
s.insert( t1 ); rest+=calc( t1 );
}
}
思路:显然的平衡树(反转操作实在是太像文艺平衡树了)。但是要对板子进行魔改。对于原来的数组 a ,记录它应该去的地方;对于平衡树数组,记录一个 minn 表示最小值。容易知道,在每次反转过后,第 \(i\) 个肯定是已经有序了,那么前面的东西事实上并没有什么用处,直接扔掉就好了。那么每次操作的时候,找剩下的最小值即可。
struct FHQTreap { int l,r,val,rnd,siz,mark,minn; }tr[N];
struct array{ int val,pos,to_val; }a[N];
bool cmp( array t1,array t2 )
{ return t1.val ^ t2.val ? t1.val<t2.val : t1.pos<t2.pos; }
bool cmp2( array t1,array t2 ) { return t1.pos<t2.pos; }
int cnt=0,rt=0,n;
int new_node( int val ) {}
void reverse( int x ) {}
void pushdown( int x ) {}
void update( int x ) {}
void split( int now,int k,int &x,int &y ) {}
int merge( int x,int y ) {}
int build( int l,int r ) {}
void dfs( int x ) {}
int findpos_min( int k,int val )
{
if ( !k ) return 0;
pushdown( k );
if ( tr[tr[k].l].minn==val ) return findpos_min( tr[k].l,val );
else if ( tr[k].val==val ) return tr[tr[k].l].siz+1;
else if ( tr[tr[k].r].minn==val ) return findpos_min( tr[k].r,val )+tr[tr[k].l].siz+1;
}
//--------------------------main----------------------------
sort( a+1,a+1+n,cmp );
for ( int i=1; i<=n; i++ ) a[i].to_val=i;
sort( a+1,a+1+n,cmp2 );
rt=build( 1,n );
for ( int i=1; i<=n; i++ )
{
int pos=findpos_min( rt,tr[rt].minn ),tx,ty,tz;
printf( "%d%c",pos+i-1,(i^n) ? ' ' : '\n' );
split( rt,pos,tx,ty ); split( tx,pos-1,tx,tz );
reverse( tx ); rt=merge( tx,ty );
}
思路:删除一段连续子序列使得剩下的最长连续递增子序列最大。所以首先可以算出来对于每个位置,前缀能延伸的最大值和后缀能延伸的最大值。那么题意就是让你找 \(l,r\) 使得 \(a_l<a_r\) 且 \(pre[l]+suf[r]\) 最大。但是复杂度是 \(O(n^2)\) 的,\(2e5\) 的数据还是过不去。考虑优化。显然,如果 \(pre[l]>=pre[l'],a[l']>=a[l]\) ,那么 \(l\) 显然是没有用的。然后每次统计答案直接在维护的队列里面 lower_bound (STL好),更新就按照同样的 \(pre[i]\) ,较小的优先即可。
终于一遍过了
Code
pre[1]=suf[n]=1;
for ( int i=2; i<=n; i++ ) pre[i]= a[i]>a[i-1] ? 1+pre[i-1] : 1;
for ( int i=n-1; i>=1; i-- ) suf[i]= a[i]<a[i+1] ? 1+suf[i+1] : 1;
int ans=0;
for ( int i=1; i<=n; i++ ) que[i]=inf;
for ( int i=1; i<=n; i++ )
{
int pos=lower_bound( que+1,que+1+n,a[i] )-que;
ans=max( ans,pos+suf[i]-1 );
que[pre[i]]=min( que[pre[i]],a[i] );
}
5.3.3 最短路例题选讲
思路:网格图,如果要让左上角没法到右下角的话,肯定满足有一条连贯的障碍,从左边或者下边到右边或者上边,这样才能做到把终点包围起来。显然是最小割,但是网络流复杂度看上去并不能过。于是考虑建模,然后问题转化成了 “左/下 \(\to\) 右/上”的最短路问题。
由于是个网格图,考虑对每个三角形建一个虚点,两个三角形相邻处的边权就是对应点连边的边权。对左边界和下边界建立超级源点,对右边界和上边界同样建立超级汇点,网格图边界上的三角形和源/汇相连,边权是边界上的边。最后跑最短路即可。
图大概长这样:Pinta 一直闪退就没画下去。
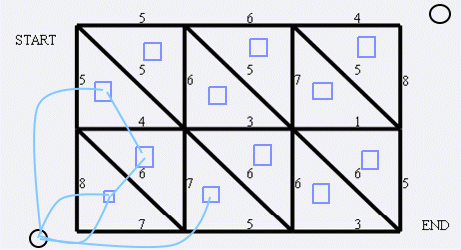
有一说一这个建图真的麻烦
这题在 UVA 上一直过不去……疯狂 TLE ,但是代码在 这道题 的洛谷和黑暗爆炸都过去了……最后发现是 ed 的值设小了,导致超级汇点编号和三角虚点混了起来……洛谷数据真的弱。
Code
//Author: RingweEH
void input()
{
for ( int i=1; i<m; i++ ) add( i*2,ed,read() );
for ( int i=2; i<n; i++ )
for ( int j=1; j<m; j++ )
{
int tmp=read(),t1=2*(i-2)*(m-1)-1+2*j,t2=2*(i-1)*(m-1)+2*j;
add( t1,t2,tmp ); add( t2,t1,tmp );
}
//------------------------------------------------------
for ( int i=1; i<m; i++ ) add( st,2*(n-2)*(m-1)-1+2*i,read() );
for ( int i=1; i<n; i++ )
for ( int j=1; j<=m; j++ )
{
int t1=2*(i-1)*(m-1)-1+2*j,t2=t1-1,tmp=read();
if ( j==1 ) add( st,t1,tmp );
else if ( j==m ) add( t2,ed,tmp );
else add( t1,t2,tmp ),add( t2,t1,tmp );
}
//-------------------------------------------------------
for ( int i=1; i<n; i++ )
for ( int j=1; j<m; j++ )
{
int t1=2*(i-1)*(m-1)-1+2*j,t2=t1+1;
int tmp=read(); add( t1,t2,tmp ); add( t2,t1,tmp );
}
}
int Dijkstra( int S ) {}
void init()
{
st=0; ed=(2*n-1)*(m-1)+1;
//Clear array & queue
}
5.4 生成树相关
5.4.0 一些性质和基本做法
切割性质
如果所有边权不相同, \(S\) 为既非空集也非全集的 \(V\) 的子集,边 \(e\) 是满足一个端点在 \(S\) 内,一个不在 \(S\) 内的所有边中权值最小的一个,则所有生成树均包含 \(e\) .
回路性质
如果所有边权均不相同,设 \(C\) 是图中任意回路,\(e\) 是 \(C\) 上权值最大的边,则 \(G\) 所有生成树均不包含 \(e\) .
增量最小生成树
从包含 \(n\) 个点的空图开始,依次加入 \(m\) 条带权边,求最小生成树权值。
每次求出新的生成树之后,把其他边删除,这样之后只需要计算 \(n\) 边图的最小生成树。根据回路性质,加入一条边之后,删除环上边权最大的边即可。复杂度 \(O(nm)\)
最小瓶颈生成树
加权无向图,求生成树使得最大边权尽可能小。
直接 \(\text{Kruskal}\) 即可得到一种方案。
最小瓶颈路
给定加权无向图上 \(u,v\) 两点,求 \(u\to v\) 的一条路径使得最长边尽可能短。
先求最小生成树,那么起点和终点在树上的路径即为所求。
次小生成树
(不严格小于)
枚举要加的新边。在最小生成树上加一条边 \(u\to v\) 后,把树上路径中最长边删除即为所求。那么可以按照最小瓶颈路的求法,\(O(n^2)\) 求两点间最大边权,\(O(m)\) 枚举 \(O(1)\) 计算答案。
最小有向生成树
给定有向带权图 \(G\) 和一个节点 \(u\) ,找一个以 \(u\) 为根节点,权和最小的树形图。(根可以到达每个点,除根外入度为1)
朱-刘 算法。
预处理,删除自环并判断无解。
给所有非根节点选择一条权值最小的入边,如果没有构成圈那么就形成了答案;否则把圈缩点,继续。
但是有个问题,如果 \(X\) 在圈中已经有了入弧 \(Y\to X\) ,收缩之后又选了 \(Z\to X\) ,那么必须把 \(Y\to X\) 减去,等价于在 \(Z\to X\) 的权值中去掉 \(Y\to X\)
UVA1494 Qin Shi Huang's National Road System
思路: 徐福太不行了只能修一条路 先求出最小生成树,然后预处理每两个点之间的路径最大边权。然后枚举每一条边作为徐福的边,用次小生成树的思想替换掉就好了。 cf在讲什么东西看不懂
Code
//Author: RingweEH
void add( int u,int v,db dis ) {}
void dfs( int u,int fat,db val )
{
for ( int i=1; i<=n; i++ )
if ( vis[i] && (i^u) ) mxc[u][i]=mxc[i][u]=max( mxc[i][fat],val );
for ( int i=head[u]; i; i=e[i].nxt )
{
int v=e[i].to;
if ( v==fat || vis[v] ) continue;
vis[v]=1; dfs( v,u,e[i].dis );
}
}
//------------------------------
int cnt=0;
for ( int i=1; i<=n; i++ )
for ( int j=i+1; j<=n; j++ )
if ( i^j ) { cnt++; r[cnt].dis=get_dis(i,j); r[cnt].num1=i; r[cnt].num2=j; }
//------------------------MST--------------------
sort( r+1,r+1+cnt );
for ( int i=1; i<=n; i++ )
fa[i]=i;
int cnt2=0; db sum=0;
for ( int i=1; i<=cnt; i++ )
{
int u=r[i].num1,v=r[i].num2; u=find(u); v=find(v);
if ( u==v ) continue;
fa[u]=v; add( r[i].num1,r[i].num2,r[i].dis ); cnt2++; sum+=r[i].dis;
if ( cnt2==n-1 ) break;
}
//-------------------Kruskal Finished----------------------
vis[1]=1; dfs( 1,0,0.0 ); db ans=0;
for ( int i=1; i<=n; i++ )
for ( int j=i+1; j<=n; j++ )
{
db B=sum-mxc[i][j],A=c[i].person+c[j].person; ans=max( ans,A/B );
}
思路:第一眼:瓶颈路??第二眼:\(n=5e4\) ???Game Over
考虑和倍增 LCA 一样的思路。令 \(fa[i][j]\) 为第 \(2^j\) 祖先,\(mxc[i][j]\) 为 \(i\to fa[i][j]\) 的最大权值。然后查询就是和LCA一样的。
人没了啊……一直是 WA ,调了半个晚上快疯掉了。留坑罢……我都把样例和 udebug 的数据全过了。
update 给你讲个笑话, for ( int i=21; i; i-- ) 和 for ( int i=21; i>=0; i-- ) 竟然是不等价的呢。
交得 UVA 都 Submit Failed 了,换了 这里 交过去的。
Code
//Author: RingweEH
void dfs( int u,int fat,int val )
{
for ( int i=head[u]; i ;i=e[i].nxt )
{
int v=e[i].to;
if ( v==fat ) continue;
fa[v][0]=u; mxc[v][0]=e[i].val; dep[v]=dep[u]+1;
dfs( v,u,e[i].val );
}
}
void LCA_init() {}
int LCA( int u,int v ) {}
void Kruskal() { }
思路:如果要最大化最小带宽,很容易想到二分最小带宽并去掉所有小于带宽的边。而让所有客户机都能收到,其实就是服务机要能到达每个客户机,要是对开头的性质熟悉的话就很容易想到树形图。那么对于二分的判定,只需要求出从 0 出发的最小树形图,判断权值和是否超过给定 \(cost\) 即可。
Code
//Author: RingweEH
int ZhuLiu() {}
bool check( int x )
{
rt=1; n=savn; newm=0;
for ( int i=1; i<=m; i++ )
if ( save[i].wide>=x ) e[++newm]=save[i];
int answer=ZhuLiu();
return answer!=-1 && answer<=cost;
}
int main()
{
for ( int cas=1;cas<=T; cas++)
{
//read & get mawid=max(e[i].wide)
//save=e
int l=0,r=mxwid,res=-1;
while ( l<=r )
{
int mid=(l+r)>>1;
if ( check(mid) ) l=mid+1,res=mid;
else r=mid-1;
}
if ( res==-1 ) { printf( "streaming not possible.\n" ); continue; }
printf( "%d kbps\n",res );
}
}
5.5 二分图匹配
UVA1006 Fixed Partition Memory Management
思路:分配内存我记得做过一次,不过是数据结构.(所以内存分配涉及众多领域是吗)
那么先重点研究一个内存区域。设这里面总共运行了 \(k\) 个程序,第 \(i\) 个程序的运行时间为 \(t_i\) ,那么这个程序的回转时间就是 \(r_i=\sum_{j=1}^{i} t_j\) 。同理得到这 \(k\) 个区域的总回转时间为 \(r=\sum_{i=1}^{k} (k-i+1)\times t_i\) ,也就是说如果程序 \(x\) 是区域 \(y\) 内倒数第 \(z\) 个执行的程序,那么它对总时间的贡献就是 \(z\times T_{x,y}\) .
然后就可以开始建模。构造二分图 \(G\) ,左部点为 \(n\) 个程序,右部点为 \((y,z)\) ,表示第 \(y\) 个区域内倒数第 \(z\) 执行的程序。左部点 \(x\) 和右部点 \((y,z)\) 连边的代价是 \(z\times T_{x,y}\) ,然后带权匹配即可(注意,KM 只能在完备匹配的前提下求解,更广泛的带权还是要费用流)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号