字符串基础算法总结
Trie
原理
不讲了吧……就是一个点对应一个字符,很基本的思路。如果不会看 这里
模板
//Author: RingweEH
//UVA1401 Remember the Word
void Insert( char *s )
{
int l=strlen(s),p=0;
for ( int i=0; i<l; i++ )
{
int ch=s[i]-'a';
if ( !tr[p][ch] ) tr[p][ch]=++tot,val[tot]=0;
p=tr[p][ch];
}
val[p]=1;
}
int Query( char *s,int st )
{
int res=0,p=0;
for ( int i=st; i<len; i++ )
{
int ch=s[i]-'a'; p=tr[p][ch];
if ( !p ) return res;
if ( val[p] ) (res+=dp[i+1])%=Mod;
}
return res;
}
int main()
{
int cas=1;
while ( scanf("%s",str )!=EOF )
{
tot=0; memset( tr,0,sizeof(tr) ); memset( val,0,sizeof(val) );
scanf( "%d",&n );
for ( int i=0; i<n; i++ ) scanf( "%s",ch ),Insert(ch);
len=strlen(str); dp[len]=1;
for ( int i=1; i<=len; i++ ) dp[len-i]=Query(str,len-i);
printf("Case %d: %d\n",cas++,dp[0] );
}
return 0;
}
练习 - UVA1462 Fuzzy Google Suggest
首先对给出的字符串集建 Trie 。对于每一次搜索操作,在 Trie 上进行两次 DFS(清理也要,数据范围三百万不可能 memset ,代码中将计算贡献和清除一起写了)
第一次 DFS 对于搜索串进行处理,如果匹配那么直接搜索,否则减少一次剩余修改次数并继续搜索。这个过程中,为了计算贡献需要打 tag ,如果是路径上经过的 Trie 节点就标记为 \(1\) ,如果是结尾就标记为 \(2\) .
第二次 DFS 对 tag 数组清除,并累加第一次出现 \(2\) 的位置的贡献。
Code
//Author: RingweEH
void Insert( char *s )
{
int p=0,l=strlen(s);
for ( int i=0; i<l; i++ )
{
int ch=s[i]-'a';
if ( !tr[p][ch] )
{
tot++; memset(tr[tot],0,sizeof(tr[tot]));
val[tot]=0; tr[p][ch]=tot;
}
p=tr[p][ch]; val[p]++;
}
}
void DFS( int p,int dep,int x )
{
if ( x<0 ) return;
if ( vis[p]==0 ) vis[p]=1;
if ( dep==len ) { vis[p]=2; return; }
int ch=s[dep]-'a';
if ( tr[p][ch] ) DFS(tr[p][ch],dep+1,x);
DFS(p,dep+1,x-1);
for ( int i=0; i<26; i++ )
if ( tr[p][i] ) DFS(tr[p][i],dep,x-1),DFS(tr[p][i],dep+1,x-1);
}
void Clear( int p,bool fl )
{
if ( vis[p]==0 ) return;
if ( fl && vis[p]==2 ) ans+=val[p],fl=0;
for ( int i=0; i<26; i++ )
if ( tr[p][i] ) Clear(tr[p][i],fl);
vis[p]=0;
}
KMP
原理
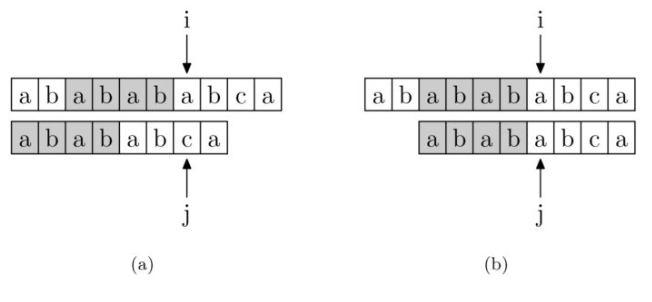
对于一个模板串 abbaaba ,如果匹配到最后一个字符失配,那么应该从模板串的第三个开始重新匹配。过程主要通过 \(nxt\) 数组实现,\(nxt[i]\) 表示以 \(s[i]\) 结尾的后缀和 \(s\) 的前缀所能匹配的最大长度( \(s\) 是模板串)(如果下标从 \(1\) 开始那么最大长度也就是最靠后的位置,通俗点说就是到 \(i\) 失配了,模板串指针就跳到这个位置继续匹配)
下图中 \(j\) 指针指向的是模板串的匹配位置。
模板
//Author: RingweEH
//P3375 【模板】KMP字符串匹配
int main()
{
scanf( "%s%s",sa+1,sb+1 );
lena=strlen(sa+1); lenb=strlen(sb+1);
for ( int i=2,j=0; i<=lenb; i++ )
{
while ( j && sb[i]!=sb[j+1] ) j=nxt[j];
if ( sb[j+1]==sb[i] ) j++;
nxt[i]=j;
}
for ( int i=1,j=0; i<=lena; i++ )
{
while ( j && sb[j+1]!=sa[i] ) j=nxt[j];
if ( sb[j+1]==sa[i] ) j++;
if ( j==lenb ) { printf("%d\n",i-lenb+1 ); j=nxt[j]; }
}
for ( int i=1; i<=lenb; i++ ) printf("%d ",nxt[i] );
return 0;
}
扩展KMP
定义母串 \(S\) 和子串 \(T\) ,设 \(S\) 的长度为 \(n\) ,\(T\) 的长度为 \(m\) ,求 \(T\) 与 \(S\) 的每一个后缀的最长公共前缀。
设 \(extend[i]\) 表示 \(T\) 与 \(S[i,n-1]\) 的最长公共前缀,要求出所有 \(extend[i](0\leq i<n)\)。
思想
从左到右依次计算 \(extend\) ,在某一时刻,设 \(extend[0\cdots k]\) 已经计算完毕,并且之前匹配过程中所达到的最远位置为 \(P\) 。所谓最远位置,就是 \(i+extend[i]-1\) 的最大值 \((0\leq i\leq k)\) ,并且设取这个最大值的位置为 \(pos\) 。
现在要计算 \(extend[k+1]\) ,根据 \(extend\) 的定义,可以推断出 \(S[pos,P]=T[0,P-pos]\) ,从而 \(S[k+1,P]=T[k-pos+1,P-pos]\) ,令 \(len=nxt[k-pos+1]\) ,分情况讨论:
- \(k+len<P\)
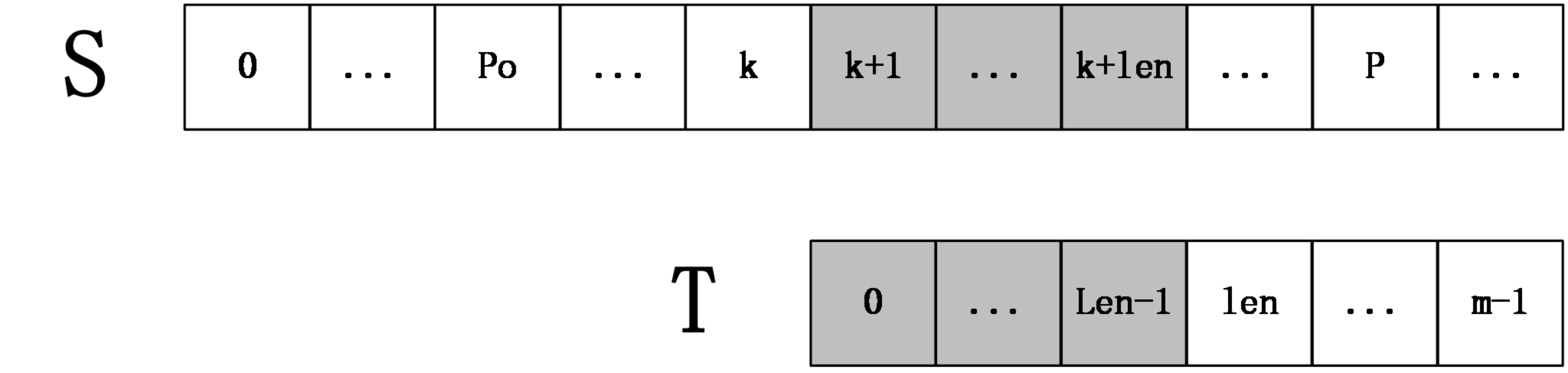
上图中,\(S[k+1,k+len]=T[0,len-1]\) ,然后 \(S[k+len+1]\) 一定不等于 \(T[len]\) ,因为如果它们相等,则有 \(S[k+1,k+len+1]=T[k+pos+1,k+pos+len+1]=T[0,len]\) ,和 \(nxt\) 数组的定义不符,所以 \(extend[k+1]=len\) .
- \(k+len>=P\)
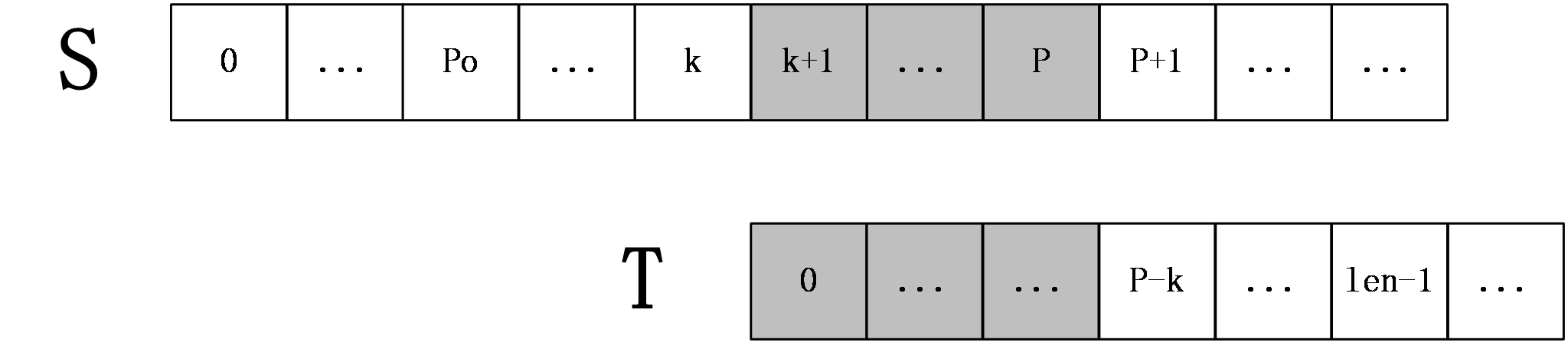
上图中,\(S[p+1]\) 之后的字符都还未进行过匹配,所以就要从 \(S[P+1]\) 和 \(T[P-k+1]\) 开始一一匹配,直到发生失配为止,当匹配完成后,如果得到的 \(extend[k+1]+(k+1)>P\) 则要更新 \(P\) 和 \(pos\) 。
练习 - UVA1358 Generator
首先对模板串 KMP 预处理。设 \(dp[i]\) 表示末尾匹配了模板串长度为 \(i\) 的前缀所需要的次数期望。
每次枚举可能出现的字符,设当前生成了 \(j\) ,且 \(j\) 不是 \(s[i+1]\) ,跳 \(nxt\) 跳到了 \(k\) ,那么匹配 \(k\) 个到匹配 \(i\) 个还需要 \(dp[i]-dp[k]\) 次。
\(f(i)=1+\sum_{i=1}^n(dp[i-1]-dp[fail(j)])/n+\dfrac{n-1}{n}f(i),dp[i]=dp[i-1]+f(i)\)
Code
//Author: RingweEH
void Get_Nxt( char *s ) {}
int main()
{
int T; scanf( "%d",&T );
for ( int cas=1; cas<=T; cas++ )
{
if ( cas>1 ) puts("");
scanf( "%d%s",&n,str+1 );
Get_Nxt(str); dp[0]=0;
for ( int i=1; i<=len; i++ )
{
dp[i]=dp[i-1]+n;
for ( int j=0; j<n; j++ )
{
if ( str[i]=='A'+j ) continue;
int p=i-1;
while ( p && str[p+1]!=(j+'A') ) p=nxt[p];
if ( str[p+1]==j+'A' ) p++;
dp[i]+=dp[i-1]-dp[p];
}
}
printf("Case %d:\n",cas );
printf("%lld\n",dp[len] );
}
return 0;
}
关于 kmp 算法中 next 数组的周期性质
约定: \(nxt[?]\) 不同于 \(nxt[i]\) ,定义为 \(nxt[i]\) 的候选项之一。
结论
对于某一字符串 \(S[1\to i]\) ,在众多的 \(nxt[i]\) 候选项中,如果存在一个 \(nxt[i]\) 使得 \(i\bmod (i-nxt[i])==0\) ,那么 \(S[1\to (i-nxt[i])]\) 可以成为 \(S[1\to i]\) 的循环节,循环次数为 \(\dfrac{i}{i-nxt[i]}\) 。
推论1
若 \(i-nxt[i]\) 可以整除 \(i\) ,那么 \(s[1\to i]\) 具有长度为 \(i-nxt[i]\) 的循环节,即 \(s[1\to i-nxt[i]]\) 。
推论2
若 \(i-nxt[?]\) 整除 \(i\) ,那么 \(s[1\to i ]\) 具有长度为 \(i-nxt[?]\) 的循环节,即 \(s[1\to i-nxt[?]]\) 。
推论3
任意一个循环节长度必定是最小循环节长度倍数。
推论4
如果 \(i-nxt[i]\) 不能整除 \(i\) ,\(s[1\to i-nxt[?]]\) 一定不能作为循环节。
扩展
- 如果 \(i-nxt[i]\) 不能整除 \(i\) ,一定不存在循环节,\(i-nxt[?]\) 一定都不可整除
- 如果 \(s[1\to m]\) 是 \(s[1\to i]\) 的循环节,\(nxt[i]\) 一定为 \(i-m\) .
- \(m-i-nxt[i],j=nxt[?]=>nxt[j]=j-m\)
AC自动机
解决问题
多个模板串匹配一个文本串。
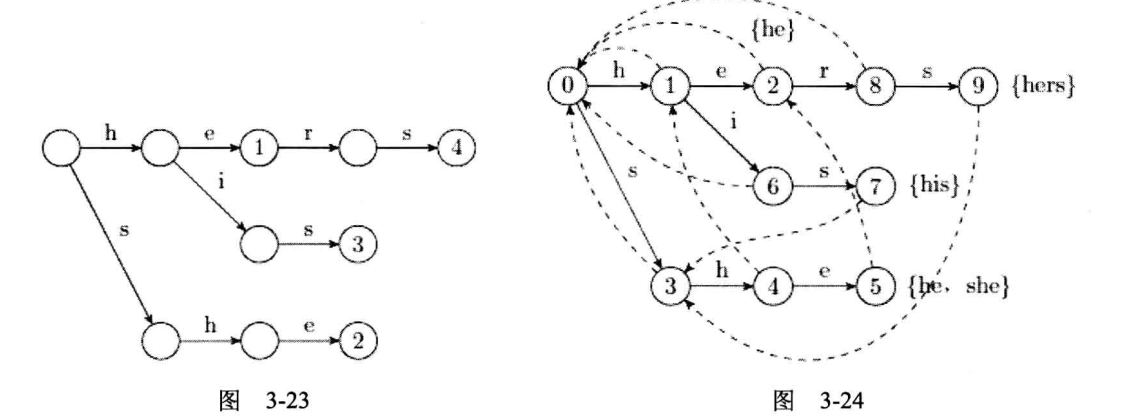
原理
大致思想是,KMP是线性的字符串加上失配边,AC自动机就是Trie加上失配边。 图解AC自动机
模板
//Author: RingweEH
void Insert( char *s )
{
int p=0,l=strlen(s);
for ( int i=0; i<l; i++ )
{
int ch=s[i]-'a';
if ( !tr[p][ch] ) tr[p][ch]=++tot;
p=tr[p][ch];
}
cnt[p]++;
}
void GetFail()
{
queue<int> q; fail[0]=0;
for ( int i=0; i<26; i++ )
if ( tr[0][i] ) fail[tr[0][i]]=0,q.push(tr[0][i]);
while ( !q.empty() )
{
int nw=q.front(); q.pop();
for ( int i=0; i<26; i++ )
if ( tr[nw][i] )
fail[tr[nw][i]]=tr[fail[nw]][i],q.push(tr[nw][i]);
else tr[nw][i]=tr[fail[nw]][i];
}
}
int Query( char *s )
{
int p=0,res=0,l=strlen(s);
for ( int i=0; i<l; i++ )
{
p=tr[p][s[i]-'a'];
for ( int j=p; j && cnt[j]!=-1; j=fail[j] ) res+=cnt[j],cnt[j]=-1;
}
return res;
}
练习 - UVA1399 Puzzle
AC自动机+DP。首先对于给出的禁止串建自动机,在每个末尾打标记,在得到 \(fail\) 指针的同时注意要传递标记。设 \(dp[u]\) 表示 Trie 树上从节点 \(u\) 往下,不经过标记的最大长度,就是子节点 \(dp\) 值取 \(\max+1\) 。然后一遍 DFS 找是否能出现循环。
Code
//Author: RingweEH
namespace ACMachine
{
int tr[N][26],cnt[N],tot,fail[N];
void Init_ACM() { tot=0; memset(tr[0],0,sizeof(tr[0])); }
void Insert( char *s ) {}
void GetFail(){}
}
using namespace ACMachine;
bool Find( int u )
{
fl[u]=1;
for ( int i=0,v; i<n; i++ )
{
v=tr[u][i];
if ( vis[v] ) return 1;
if ( !fl[v] && !cnt[v] )
{
vis[v]=1; if ( Find(v) ) return 1; vis[v]=0;
}
}
return 0;
}
int DFS( int u )
{
if ( vis[u] ) return dp[u];
vis[u]=1; dp[u]=0;
for ( int i=n-1; i>=0; i-- )
if ( !cnt[tr[u][i]] )
{
int tmp=DFS(tr[u][i])+1;
if ( dp[u]<tmp ) dp[u]=tmp,ans[u][0]=tr[u][i],ans[u][1]=i;
}
return dp[u];
}
void Write( int u )
{
if ( ans[u][0]==-1 ) return;
printf("%c",ans[u][1]+'A' ); Write(ans[u][0]);
}
int main()
{
//freopen( "exam.in","r",stdin );
int T; scanf("%d",&T );
while ( T-- )
{
Init_ACM(); scanf("%d%d",&n,&m);
while ( m-- ) scanf("%s",str),Insert(str);
GetFail();
memset(fl,0,sizeof(fl)); memset(vis,0,sizeof(vis)); vis[0]=1;
if ( Find(0) ) { puts("No"); continue; }
memset( vis,0,sizeof(vis) ); memset( ans,-1,sizeof(ans) );
if ( DFS(0)==0 ) puts("No");
else Write(0),puts("");
}
return 0;
}
- AC自动机+线段树优化DP :UVA1502 GRE Words
Manacher
解决问题
最长回文子串:给定一个字符串,求它的最长回文子串长度。
原理
一个很简单的想法是枚举对称中心,向两边扩展。这样做的缺陷在于回文子串长度的奇偶性导致对称轴不确定。所以可以在原串首尾和两两字符之间插入一个无关字符,这样串长都是奇数且原有回文性质不变。
定义:回文半径:一个回文串中最左(右)位置的字符到其对称轴的距离 ,用 \(p[i]\) 表示第 \(i\) 个字符的回文半径。例如:
char : # a # b # c # b # a #
p[i] : 1 2 1 2 1 6 1 2 1 2 1
p[i] - 1 : 0 1 0 1 0 5 0 1 0 1 0
i : 1 2 3 4 5 6 7 8 9 10 11
显然,最大的 \(p[i]−1\) 就是答案。
插入完字符之后对于一个回文串的长度为 原串长度 \(\times 2+1\) ,显然相等。
这样问题就转换成了怎样快速的求出 \(p\) 。用 \(mx\) 表示当前所有字符产生的最大回文子串的最大右边界, \(id\) 表示产生这个边界的对称轴位置。
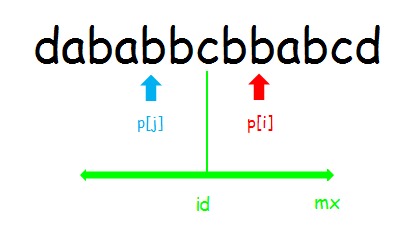
设已经求出了\(p[1...7]\) ,当 \(i<mx\) ,因为 \(id\) 被更新过了,而 \(i\) 是 \(id\) 之后的位置,第 \(i\) 个字符一定落在 \(id\) 右边。
记串 \(i\) 表示以 \(i\) 为对称轴的回文串,\(j\) 和 \(id\) 同理。
情况1:i < mx
利用回文串的性质,对于 \(i\) ,可以找到一个关于 \(id\) 对称的位置 \(j=id\times 2−i\) ,进行加速查找
(1) :串 \(j\) 在串 \(id\) 内部,显然 \(p[i]=p[j]\) 且串 \(i\) 不能再扩张(否则 \(p[j]\) 也可以)
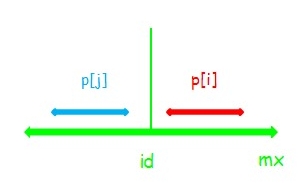
(2) :串 \(j\) 左端点与串 \(id\) 左端点重合,此时 \(p[i]=p[j]\) 但串 \(i\) 可以再扩张。
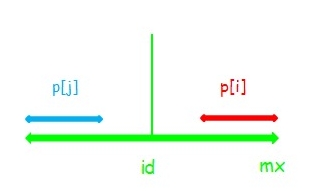
(3) :串 \(j\) 左端点在串 \(id\) 左端点左侧。此时 \(p[i]=mx-i\) ,只能确定串 \(i\) 在 \(mx\) 以内部分回文,串 \(i,j\) 不一定相同。
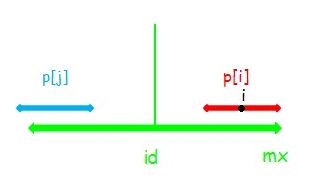
这时串 \(i\) 是不可以再向两端扩张的。如果可以,如下图,(这里 \(p[j]>p[i]\) ,那么 \(p[j]\ge p[i]+1\) ,截取 \(a,b\) 使得和扩张 \(1\) 之后的 \(i\) 相同显然不会影响正确性),有 \(d=c\) ,所以 \(c=b\) ,又因为 \(a=b\) 所以 \(a=d\) ,这样串 \(id\) 就能扩张,矛盾。
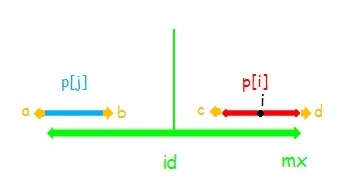
情况2:i >= mx
显然 \(p[i]=1\) .
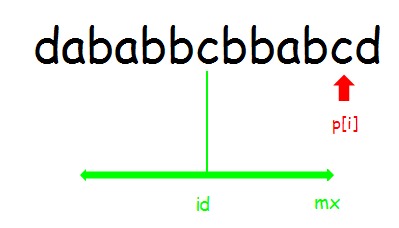
注意,这里的 \(p[i]\) 的情况讨论均指“可以从 \(id\) 和 \(mx\) 中继承”的部分而不是最终的结果,也就是已经处理过的不会再进行处理,要处理一定是往后拓展。
模板
//P3805 【模板】manacher算法
//Author: RingweEH
const int N=2.2e7+10;
int len,pos[N];
char s[N],str[N];
void Init()
{
len=strlen(s); str[0]='@'; str[1]='#'; int j=2;
for ( int i=0; i<len; i++ ) str[j++]=s[i],str[j++]='#';
str[j]='\0'; len=j;
}
int main()
{
scanf("%s",s); Init();
int ans=-1,mx=0,id=0;
for ( int i=1; i<len; i++ )
{
if ( i<mx ) pos[i]=min(pos[id*2-i],mx-i);
else pos[i]=1;
while ( str[i+pos[i]]==str[i-pos[i]] ) pos[i]++;
if ( pos[i]+i>mx ) mx=pos[i]+i,id=i;
ans=max(ans,pos[i]-1);
}
printf("%d\n",ans );
return 0;
}
练习 - UVA1470 Casting Spells
其实就是找连续出现两次的偶长度回文串。
暴力做法是枚举并判断右边是否也是相同的回文串,考虑 Manacher 的性质。
设现在在位置 \(i\) ,由于 Manacher 把偶数串转化为了奇数,所以要求 \(i\) 是分隔符 # 。当回文半径为 \(4\) 的倍数时,左半边的串长就是偶数,中心为 \(i-r/2\) (其中 \(r\) 是回文半径)。只要左半边中心的回文半径不小于 \(i-r/2\) 那么就是回文串。
Code
//Author: RingweEH
const int N=3e5+10;
int n,pos[N<<1],len;
char s[N],str[N<<1];
void Init()
{
int j=0; len=strlen(s);
for ( int i=0; i<len; i++ ) str[j++]='#',str[j++]=s[i];
str[j++]='#'; len=j;
}
int main()
{
//freopen( "exam.in","r",stdin );
int T; scanf("%d",&T);
while ( T-- )
{
scanf("%s",s); Init();
int mx=0,id=0,ans=0;
for ( int i=0; i<len; i++ )
{
if ( i<mx ) pos[i]=min(pos[2*id-i],mx-i);
else pos[i]=1;
while ( i+pos[i]<len && i-pos[i]>=0 && str[i+pos[i]]==str[i-pos[i]] )
{
int x=pos[i];
if ( str[i]=='#' && x%4==0 && pos[i-x/2]>=x/2 ) ans=max(ans,x);
pos[i]++;
}
if ( i+pos[i]>mx ) mx=i+pos[i],id=i;
}
printf( "%d\n",ans );
}
return 0;
}
最小表示法
定义
字典序最小的循环同构串。(就是整体左移或右移,环状)
原理
考虑两个字符串 $A,B $ ,在 \(S\) 中的起始位置为 \(i,j\) ,且前 \(k\) 位相等。 如果 \(A[i+k]>B[j+k]\) ,那么对于任何一个字符串 \(T\) ,开头位于 \(i\to i+k\) 之间,一定不会成为最优解。所以 \(i\) 可以直接跳到 \(i+k+1\)
复杂度 \(O(n)\).
模板
//UVA719 Glass Beads
//【模板】最小表示法
//Author: RingweEH
const int N=3e4+10;
int n,len;
char str[N];
int main()
{
//freopen( "exam.in","r",stdin );
int T; scanf("%d",&T);
while ( T-- )
{
scanf("%s",str); len=strlen(str);
int k=0,i=0,j=1;
while ( k<len && i<len && j<len )
{
int tmp=str[(i+k)%len]-str[(j+k)%len];
if ( tmp==0 ) k++;
else
{
if ( tmp<0 ) j+=k+1;
if ( tmp>0 ) i+=k+1;
if ( i==j ) i++;
k=0;
}
}
printf("%d\n",min(i,j)+1 );
}
return 0;
}
参考
- OI-Wiki
- exKMP
- 找不到 Manacher 配图的作者博客了
/shake


 浙公网安备 33010602011771号
浙公网安备 33010602011771号