[CF1464F]My Beautiful Madness

做题时间：2022.10.11

$【题目描述】$

给定一棵 $n(n\leq 2\times 10^5)$ 个点的树，定义树上一条路径的 $d$ 邻居为一个点集 $S$，满足 $x\in S$ 当且仅当存在一个路径上的点 $y$ 使得 $dis(x,y)\leq d$

现在有 $m$ 次操作，维护一个初始为空的集合 $P$，有三种操作：

1. 在 $P$ 中加入一条路径
2. 在 $P$ 中删除一条路径
3. 询问 $P$ 中所有路径的 $d$ 邻居交集是否为空

$【输入格式】$

第一行两个整数 $n,q$

接下来 $n-1$ 行每行两个整数 $u,v$ 表示树上的一条边 $(u,v)$

接下来 $q$ 行每行二或三个整数，表示一次操作，具体而言：

1. 1 u v 表示在 $P$ 中加入一条路径 $(u,v)$
2. 2 u v 表示在 $P$ 中删除一条路径 $(u,v)$
3. 3 d 表示询问 $P$ 中所有路径的 $d$ 邻居交集是否为空，若不为空输出Yes，否则输出No

$【输出格式】$

对于每一个操作3，输出一行Yes或No

$【考点】$

欧拉序、树上差分、线段树、树状数组

$【做法】$

好神仙的树上问题/se

首先处理路径问题，一般用lca或端点来代表一条路径，后分类讨论，这道题就可以考虑用lca代表一条路径。

然后看能否简化一下询问的东西，能不能找到某个点，使得路径有交集就一定包含这个点，发现还真有：深度最大的路径的lca的 $d$ 级祖先，设他为 $u$，这个用multiset 什么维护一下就行。

若 $u$ 是所有路径的 $d$ 邻居，那么交集不为空。然后向上再走 $d$ 步，得到点 $v$，可以发现若存在路径在 $v$ 的子树之外，那么肯定不满足要求，这个问题可以使用 树上差分+树状数组 解决。具体而言，将树上节点按照欧拉序排成一个序列，然后每次加入路径就在对应的 $L$ 处+1/-1，由于 $v$ 子树的欧拉序是连续的，因此可以直接查询 $[L_v,R_v]$ 的区间和是否为当前路径总数。

保证了路径全部都与 $v$ 子树有交集，接下来，所有路径分为两类：

1. lca在 $v$ 子树之外，伸了条链进 $v$ 子树的路径肯定满足要求（如图红色的路径）：

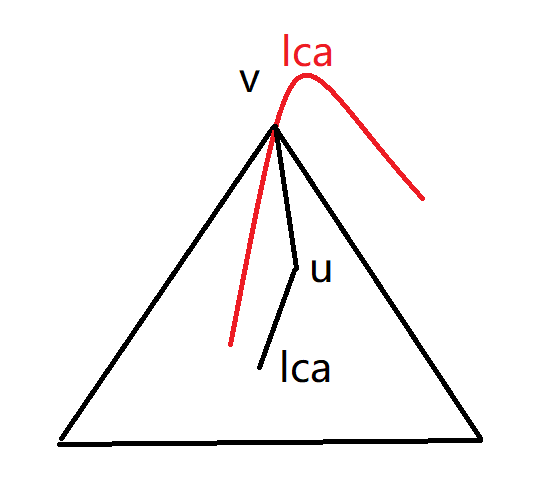
2. 整条路径均在 $v$ 的子树之内的，他们的lca与 $u$ 的距离肯定不能超过 $d$，转化一下就变成在一个子树内查找距离 $u$ 最远的点的距离，可以联想到直径的两端点， 于是再转化成维护子树内的直径，可以同样用欧拉序展开整棵树后，用线段树维护 ，每个节点存下对应区间内的直径两端点，pushup的时候用左右儿子共四个端点组合成新的最大直径即可。算出两端点后判断与 $u$ 的距离是否 $\leq d$

然后就做完力/zhq/zhq/zhq

写的时候注意下树状数组和线段树要开两倍（dfs序除外）

写起来又臭又长

$【代码】$

#include<bits/stdc++.h>
#define lowbit(i) i&(-i)
#define ls(k) k<<1
#define rs(k) k<<1|1
#define It multiset<pair<int,int> >::iterator
using namespace std;
const int N=2e5+50,inf=1e9;
struct edge{
	int to,nxt;
}a[N<<1];
int head[N],f[N][30],Eul[N<<1],dep[N],cnt,n,q;
int L[N],R[N],sum,tot;
multiset<pair<int,int> > s;
namespace Tree{
	void dfs(int u,int fa)
	{
		Eul[++tot]=u,L[u]=tot; 
		dep[u]=dep[fa]+1,f[u][0]=fa;
		for(int i=1;i<=25;i++) f[u][i]=f[f[u][i-1]][i-1];
		for(int i=head[u];i;i=a[i].nxt){
			int v=a[i].to;
			if(v!=fa) dfs(v,u); 
		}
		R[u]=++tot;
	}
	int lca(int x,int y)
	{
		if(dep[x]<dep[y]) swap(x,y);
		for(int i=25;i>=0;i--){
			if(dep[f[x][i]]>=dep[y]) x=f[x][i];
		}
		if(x==y) return x;
		for(int i=25;i>=0;i--){
			if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
		}
		return f[x][0];
	}
	int Jump(int x,int d)
	{
		for(int i=25;i>=0;i--){
			if((1<<i)<=d&&f[x][i]) x=f[x][i],d-=(1<<i); 
		}
		return x;
	}
	int dis(int x,int y)
	{
		if(x==0||y==0) return -inf;
		int l=lca(x,y);
		return dep[x]+dep[y]-2*dep[l];
	}
}
namespace FWT{//树状数组
	int c[N<<1];
	inline void Add(int x,int y){for( ;x<=2*n ;x+=lowbit(x)) c[x]+=y;}
	inline int Query(int x)
	{
		int sum=0;
		for( ; x; x-=lowbit(x)) sum+=c[x];
		return sum;
	}
}
namespace Seg{//线段树
	struct Node{
		int x,y;
		Node(){x=0,y=0;}
		Node operator +(const Node &b)const{//线段树pushup
			int maxn=-inf,nx=0,ny=0;
			int node[5]={x,y,b.x,b.y};//左右儿子四端点算最长直径
			for(int i=0;i<4;i++){
				for(int j=i+1;j<4;j++){
					int d=Tree::dis(node[i],node[j]);
					if(d>maxn) maxn=d,nx=node[i],ny=node[j];
				}
			}
			Node t;
			t.x=nx,t.y=ny;
			return t;
		}
	}tree[N<<4];
	int tot[N<<4];//记录每条路径出现次数
	#define x(k) tree[k].x
	#define y(k) tree[k].y
	
	void Modify(int k,int l,int r,int p,int v)
	{
		if(l>p||r<p) return ;
		if(l==r){
			if(v) x(k)=Eul[l],y(k)=Eul[l];
			else x(k)=y(k)=0;
			return ;
		}
		int mid=(l+r)>>1;
		if(p<=mid) Modify(ls(k),l,mid,p,v);
		else Modify(rs(k),mid+1,r,p,v);
		tree[k]=tree[ls(k)]+tree[rs(k)];
	}
	Node Query(int k,int l,int r,int x,int y)
	{
		if(l>y||r<x){Node t;return t;}
		if(x<=l&&r<=y) return tree[k];
		int mid=(l+r)>>1;
		Node ans;
		if(x<=mid) ans=Query(ls(k),l,mid,x,y);
		if(y>mid) ans=ans+Query(rs(k),mid+1,r,x,y);
		return ans;
	}
	void Erase(int p)//删除一条路径
	{
		tot[p]--;
		if(!tot[p]) Modify(1,1,2*n,L[p],0);
	}
	void Add(int p)//增加一条路径
	{
		tot[p]++;
		if(tot[p]==1) Modify(1,1,2*n,L[p],1);
	}
}
 
inline int Read()
{
	int x=0;
	char ch=getchar();
	while(!isdigit(ch)) ch=getchar();
	while(isdigit(ch)){
		x=(x<<1)+(x<<3)+ch-48;
		ch=getchar();
	}
	return x;
}
void add(int u,int v)
{
	cnt++;
	a[cnt].to=v;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
bool solve(int d)
{
	It it=s.end();it--;
	pair<int,int> now=*it;
	int u=Tree::Jump(now.second,d);
	int v=Tree::Jump(u,d);
	int t=FWT::Query(R[v])-FWT::Query(L[v]-1);
	
	if(sum!=t) return false;
	Seg::Node ans=Seg::Query(1,1,2*n,L[v],R[v]);
	if(Tree::dis(ans.x,u)<=d&&Tree::dis(ans.y,u)<=d) return true;
	return false;
}
int main()
{
	n=Read(),q=Read();
	for(int i=1;i<n;i++){
		int u=Read(),v=Read();
		add(u,v),add(v,u);
	}
	Tree::dfs(1,0);
	while(q--){
		int opt,u,v,d;
		scanf("%d",&opt);
		if(opt==3){
			scanf("%d",&d);
			if(solve(d)) printf("Yes\n");
			else printf("No\n");
		}
		else{
			scanf("%d%d",&u,&v);
			int l=Tree::lca(u,v);
			if(opt==1){
				FWT::Add(L[u],1),FWT::Add(L[v],1);
				FWT::Add(L[l],-1),Seg::Add(l);//差分
                
				s.insert(make_pair(dep[l],l)),sum++;
			}
			else{
				FWT::Add(L[u],-1),FWT::Add(L[v],-1);
				FWT::Add(L[l],1),Seg::Erase(l);//差分
				s.erase(s.lower_bound(make_pair(dep[l],l))),sum--;
			}
		}
	}
	return 0;
}