计数排序

 

算法思想

计数排序适用于n个待排序元素都是在0到k区间内的整数,算法步骤如下:

• 统计待排序数组在区间点的重复次数
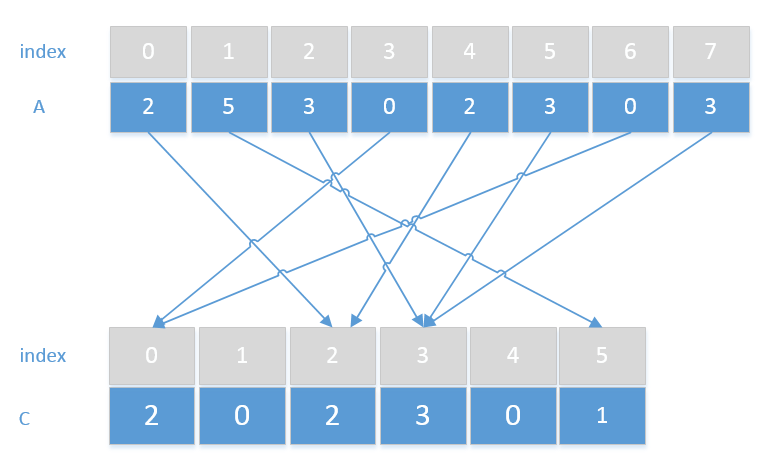
  例如:有待排序数组A{2,5,3,0,2,3,0,3},可以看出待排序数组中的元素都位于区间[0,5]内,现在使用辅助数
  组C[6],来统计数组A在这个区间每个点的重复次数:
  
  首先先将辅助数组C全部置为0,然后遍历待排序数组A,将数组A的元素值作为辅助数组C的下标,然后将辅助数组
  C中对应下标的元素值加1,这样即可统计出待排序数组在区间[0,5]内每个点出现的次数

• 将统计的区间重复次数转换为待排序元素在有序数组中的位置
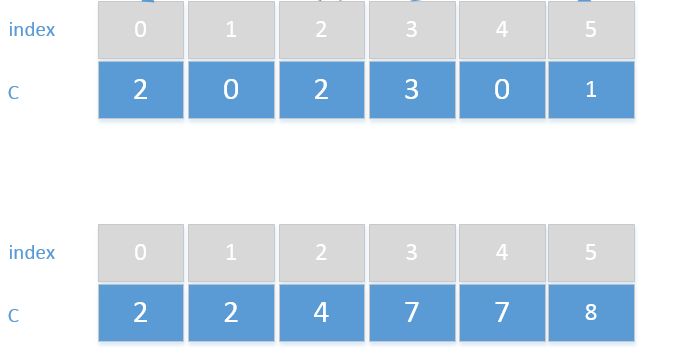
  在上一步统计待排序数组在区间点的重复次数时,待排序数组中所有数值相同的元素个数均被统计出来,所以可以
  对辅助数组C进行从左到右遍历,并依次执行C[i]+=C[i-1],也就是将统计点i前面的i-1统计点的次数加到统计
  点i上,就可以推算某个统计点上最后一个元素在有序数组中的位置(如果待排序数组有多个重复元素):
  

• 根据待排序元素有序时在数组中的位置得出有序数组
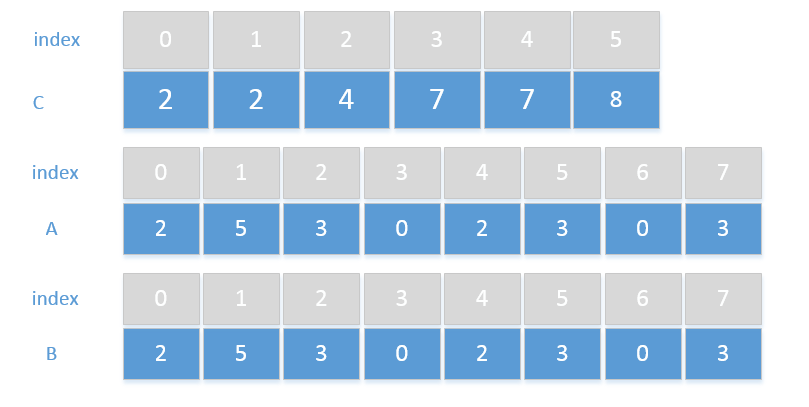
  从后向前遍历待排序数组A,并对数组A中的每个元素进行如下操作:
  取出当前正在遍历的元素x,并取出辅助数组中对应的C[x]值,此时C[x]的值就是数组A中元素x排序后在数组A中
  的位置,此时使用一个排序输出数组B来存放排序结果

   
  
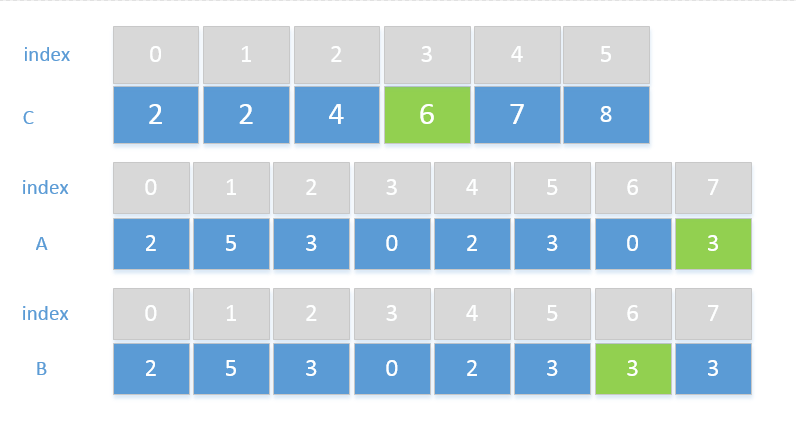
  取A[7]得到待排序元素3,取C[A[7]]得到位置7,那么元素3应该有序数组中第7个元素位置,但数组下标以0开始
  所以元素3位于有序数组中下标为6的位置,所以应该将A[7]赋值给B[C[A[7]]],另外还需要将C[A[7]]自减1,
  因为待排序数组中可能会有多个值与A[7]相同的元素,那么这些相同的元素应该排在输出数组B中下标5的位置
  
  后面就懒得画图了

代码实现

  //************************************************************************
// 函数名称: CountSort
// 函数功能:  计数排序
// 返回值:   bool:成功返回true,否则返回false
// 参数:     int * pUnsortAry:待排序数组
// 参数:     int * pOutputAry:输出数组
// 参数:     int nArySize:数组大小
// 参数:     int nMaxValue:待排序元素的最大值
// 注意:
//************************************************************************
bool CountSort(int * pUnsortAry, int * pOutputAry, int nArySize ,int nMaxValue)
{
  if (nMaxValue < 0 || pUnsortAry == nullptr || pOutputAry == nullptr)
  {
    return false;
  }

  int * pTempAry = new int[nMaxValue+1];
  if (pTempAry == nullptr)
  {
    return false;
  }

  memset(pTempAry, 0, sizeof(int)*(nMaxValue + 1));

  /*统计待排序数组在区间点的重复次数*/
  for (int nIndex = 0; nIndex < nArySize; nIndex++)
  {
    pTempAry[pUnsortAry[nIndex]]++;
  }

  /*将统计的区间重复次数转换为待排序元素在有序数组中的位置*/
  for (int nIndex = 1; nIndex < nArySize-2; nIndex++)
  {
    pTempAry[nIndex] += pTempAry[nIndex - 1];
  }

  /*输出排序结果到输出结果数组*/
  for (int nIndex = nArySize - 1; nIndex >= 0; nIndex--)
  {
    pTempAry[pUnsortAry[nIndex]]--;
    pOutputAry[pTempAry[pUnsortAry[nIndex]]] = pUnsortAry[nIndex];
  }

  delete[] pTempAry;
  return true;
}

时间复杂度

可以直接看出计数排序的时间复杂度为O(n)

稳定性

因为在输出排序结果的过程中,for循环的遍历是待排序数组从后向前遍历的,有这句代码可以看出:

pOutputAry[pTempAry[pUnsortAry[nIndex]]] = pUnsortAry[nIndex];

如果有相同的元素值那么靠数组尾部的元素值也排在输出数组的靠尾部的地方,所以计数排序是稳定的,如果我们
对待排序数组从前向后遍历,如果有相同元素,排在待排序数组前面的元素将会被排到输出数组的尾部,这是不稳定
的