暑假集训周复盘

每周六晚上进行完善，加深对题做法的记忆。

第一周

周一

上午突发恶疾，没打模拟赛，但是补了所有题。
这一场是倒序放题的。

A

我们考虑：
1.每一次瞬移之间是独立的。所以把瞬移分成logV层。
2.预处理出来第k层内部，每个点i向左向右最远能走到哪个点（即预处理联通块），就是l[k][i]和r[k][i]。
3.我们考虑把前缀和后缀拼凑，以得到是否可行。设pre[sta]和suf[sta]分别为从头往后走，走过了状态为sta的层，所能走到的最靠后的点，和从后往前走，走过了状态为sta的层，所能走到的最靠前的点。
4.这个的转移不难，就是多枚举一层，然后在这一层往后跑，suf同理。
5.合并答案，枚举状态sta，假如pre >= suf，那么所有点都是可以完成的，直接return 0了。
6.否则如果pre[sta]和suf[sta]在一个联通块里面，就用差分给这个块的点答案+1，最后再跑一遍前缀和。原理是从终点往前跑和从起点往后跑是一样的。

B

注意力题。
1.我们发现，求值不好解决，考虑用二分转化成判定问题。就是把底层每个点如果大于等于mid就计成1，否则是0，然后判断顶上的颜色。然后如果是1就r = mid + 1，否则是l = mid - 1，过程中记录ans。
2.我们观察发现，如果有长度大于1的同色连续段，那么离中间最近的连续段的颜色就是顶的颜色。这个是找规律发现的。
3.如果没有连续段，就是1和0哪个个数多选哪个。

C

奇特小题。
1.我们观察这个3n，发现3n=n+2n，即如果有一个边数为n的极大边匹配，那么剩下的可以是一个点数为n的极大独立集。可以用反证法证明。
2.所以发现该问题一定是有解的。我们尽力匹配，如果配够n就输出，否则输出独立集。

D

找规律小题。不提。

周二

这场打得相当不好了，A是简单小DP，但是是反向可行性DP，设状态思路一直不对；C是中秋节时候和寒假都练过的字符串根号分治，但是没做出来。要开始进入状态了。

A

这种时候，一般要考虑可行性DP。
1.设f[i][j][k]为跑了i个大圈，j个小圈，过了k次河时的最小所需马匹数。
2.发现贪心的一点：把过河放在最前面最优。
3.转移就是再枚举一个x,y,z作为新的一匹马的数据。发现x只有两种取值，y最多5种，z最多7种。
4.根据三元均值不等式可得，外层循环复杂度是1e6；内层根据第三条，是70，而且实际上小于70。肯定是能过的。

B

有点困难的一个数论题。当时赛时弃掉是正确的。
1.先考虑根号复杂度分解质因数的。
2.我们分解质因数，把每个质因子的指数对3取模，因为只要一边1个，另一边2个或者反过来，就能凑出来完全立方数。
3.所以把指数取模后，对于一个数\(a_i\)得到它对应的x，然后在分解过程中进行操作，得到对应的y。
4.维护两个map，分别记录x与y的对应关系，和x在序列中出现的次数。
5.每个数分解完了，把x放进一个队列里，然后从头往后扫，每次选择x和tox中个数更多的一个，然后把两个的数量都改为0。
6.考虑低复杂度地分解质因数。我们只枚举\(a_i\)的立方根以内的质因子。记分解完剩下的数为m。分三类讨论：
6.1. m=1，则原数是完全立方数，这样的数显然是只能取一个的。所以ans=1然后continue。
6.2. m=ab(a $\ne $ b)或m是质数，则给x乘上m，y乘上\(m^2\)。
6.3. m=\(a^2\)，是完全平方数则x乘上m，y乘上\(\sqrt m\)。

C

这个真是简单题。发现所有查询字符串总长度为n的量级。
1.考虑阈值分治，先预处理文本串哈希。
2.把所有长度小于等于B的子串的哈希值存到unordered_map里面。
3.查询如果长度小于等于B直接查map。
4.如果长度大于B，就扫一遍。这种情况最多\(\frac{n}{B}\)个。
5.复杂度理论上是\(O(nB+\frac{n^2}{B})\)，但是unordered_map常数太大了，所以B设30左右跑得最快。

D

比较勾史。

周三

排名上看还行，但是A离正解其实很近了。D改得还是有点不明所以。

A

1.首先发现是要把区间合并。设\(f_{i,j,k}\)为[i,j]中，做完剩下k点魔力值时最小的魔力值消耗。
2.转移分两种：枚举断点再把两边魔力值加起来，和往后面延伸一格，消耗掉一些魔力值。
3.复杂度其实是五次方，但是常数小，能过。

B

题面太勾史了，不看。

C

1.特性S、T连边：考虑让T当根，小N显然要往下走，设\(f_u\)为从u出发，然后走回u所需的最小操作次数。对于所有的\(v \in son[u]\)，小N显然要往\(f_v\)最大的走，所以要把这一条砍掉。然后就走到次大的，再把所有的儿子都砍掉，再把走回来的这条边补上，就是次大\(f_v\) + \(son[u]\)。
2.答案是什么呢，因为走回来u之后u是没有儿子的，所以只能往上面走，答案就是\(f_S\)。
3.考虑正解。还是要dfs求出来f数组，然后考虑求出来一个\(g_u\)表示u的儿子往上走到根，有多少旁支。
4.我们考虑二分一个阈值k，代表小Y最多操作k次。小N可以先往上走再往下走，所以从S开始往上跳，每次遍历儿子，记录当前花费used和当前小Y轮了几轮sum。
5.一句关键代码用来判断删不删(u,v)：if(f[v] + g[u] + used + 1 - (u != S) > mid)cnt++;
解读一下：就是从u走下去走到v，在v里面转一圈，代价+f[v]；然后把旁支减掉，代价加+g[u]；然后加上使用过的代价used；然后+1，恢复从v到u的边来走向父亲；如果这个节点不是起点，那么走上来的时候小N已经断掉一条边了，就-1。
6.然后每次判定cnt+used是否小于等于mid和sum，可以认为是把轮数攒起来使用的。

D

1.首先设\(f_{i,j,t,u}\)代表[i,j]，i-1和j+1都是在整段[i,j]被删掉之后删掉的，j+1右边第一个没有删掉的地雷是t，[i,j]中所有u左边的点都在u之前被删掉了时的最小代价。
2.考虑转移，枚举断点k为区间里最晚删除的点，就是分成两块，再加上\(val(i-1, k, j+1, t)\)。
有点不想写这题题解，因为没有搞懂。但是学习了一下增加限制的思维。

周四

改了一下前几天的题，然后写了两道DP专题的题。
A是简单的，就是拆贡献，把每个数的贡献区间算出来，线段树维护即可。
B比较像可行性DP，就是设\(f_{i,j}\)为走到i召唤了j只鸟，最多还剩多少魔法。魔法上限是能根据鸟只数算出来的。
最后注意复杂度分析，三轮循环分别是n，m, 一个点的鸟数，总复杂度是\(\sum m \times c_i = m^2\)。

周五

A

1.注意不要把题读错。
2.画一个图玩一玩，发现每一条边如果端点编号差值是d，那么会生成\(gcd(n,d)\)个联通块，最少需要\(n - gcd(n,d)\)条边。
3.然后发现一个联通块可以被缩成一个点来处理，所以每次操作完\(n = gcd(n,d)\)。
4.在过程中记录答案即可。

B

1.我们发现，答案应当是每个数前面比自己大的数的个数的最大值。因为每轮冒泡排序必然会把一个比\(a_i\)大的数换到它后面。
2.问题转化为，构造一个排列b，使得\(b_i < i\)，且其中最大值为k，求这样的排列有几个。
3.\(i \le k\)的点随便选，后面的就是\((k+1)^{n-k} - k^{n-k}\)。然后再搞一下就做完了。

C

好题，在我的奋战下终于改出来了。
1.先考虑k=1的。贡献思想，看每一个点会被多少个矩形覆盖即可。
2.再考虑k=2的。观察式子：\((a+b+c)^2=a^2 + b^2 + c^2 +2ab +2bc +2ac\)。前面\(1^2\)的部分就是把k=1的加起来就行。后面的要这么做：
考虑计算一组点对(i,j)会被几个矩形覆盖，先假设它是顺序对，逆序对就把序列翻转一下就行。
个数显然是：\(i \times a_i \times (n - j) \times(n - a_j)\)。类似二维偏序，把每个点的贡献存到树状数组\(a_i\)的位置上，然后查询和，再乘上自己的系数。
3.分析k=3的。\((a+b+c)^3 = a^3 + b^3 + c^3 + 6a^2b +6a^2c+ 6b^2c + 6abc\)。发现只有6abc是需要进行新的处理的。
4.有两种本质不同的情况：

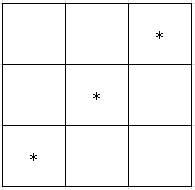
这个直接枚举中间的点，树状数组扫两遍就行。

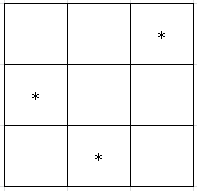
这个类型的，我们翻转一下，让右下角的是k，上面的是i，左边的是j，容易发现个数是\(i \times a_j \times (n - k + 1) \times (n - a_k + 1)\)。
考虑首先扫到的是i，就给线段树中的\(a_i\)的x单点加，然后扫到的是j，就给\([a_j + 1, n]\)的k区间加。查询时查的是\(\sum k \times x\)。
然后这个上下翻、左右翻、上下左右都翻，就把所有的做完了。

D

太几把了。

周六

A

脑子不够，DS来凑。
1.我们考虑从根开始，每次向下dfs时，使用dfs序线段树维护一个点到其他点的距离。
2.维护一下最大值下标，然后如果最大值不到d就是-1。
3.然后查询一下这两个点的LCA，根据这个来决定要从哪个点往上跳d。

B

我假到家的几把算法过了。
1.考虑设\(g_{i,j}\)为\(a_i\)左边的离\(a_i\)最近的，第j位为1的元素的下标。求这个是容易的。
2.设\(f_{i,j}\)为\(a_i\)左边的离\(a_i\)最近的，第j位为1的，且可以到达i的元素的下标。
3.f的转移需要一点技术。

4.先考虑枚举一个位k，且\(a_i\)的第k位不为0。
如果选择一个中转站，就必须保证：i可以到中转站，且中转站可以到\(f_{i,j}\)。
所以中转时就是\(\large f_{g_{i,k},j}\)。
再考虑不中转的，就是\(g_{i,k}\)的第j位为1，保证符合了状态定义。

5.考虑查询。就是枚举l和r的每一位i，如果\(a_l\)的第i位为1，且\(f_{r,i} \ge l\)，发现l一定可以到达\(f_{r,i}\)，那么就可行。

C、D

先咕了。

第二周

周一

打得一般般。

A

1.难点其实是去重。
2.考虑设\(f_{i,j,k}\)为到第i个盒子，放了j块金牌，其中第i个盒子放了k块的方案数。
3.首先需要给a数组排序来去重，其次放置完金牌的金牌盒应当仍然单调不降。
4.所以转移就是一直给后面的放，保证后面的不小于前面的。
5.把它转成填表法，然后前缀和优化即可。

B

还没改。

C

线段树优化DP。这种做法还是比较常见。
1.\(\large f_i = \max f_{j-1} + cost(j,i)\)。对于cost，考虑和基站选址一样拆贡献做。
2.max具有单调性，设\(Ll_i，Lr_i\)使得\([Ll_i，Lr_i]\)中的点为左端点，i为右端点的区间max是可以给i作出贡献的。\(Rl_i，Rr_i\)同理。
3.我们发现，当r在\([i，Rl_i)\)中时，max只能由左边区间提供，l在\([Ll_i，Lr_i]\)时有贡献。
4.当r在\([Rl_i，Rr_i]\)中时，max可以由右边区间提供，l可以新增\((Lr_i，i]\)这一段区间的贡献。
5.当r在\(Rr_i\)后面时，没有贡献，把前面的贡献清除掉就行。
6.我们注意到，j的贡献是加在\(f_{j-1}\)上面的，所以考虑把所有的查询区间右移一位，修改区间位置不变。
7.求解前面那四个东西，用二分+ST表即可。

周二

打得很几把，没有想出来任何有思维含量的东西。

A

观察发现，答案应该是排序后的一段后缀。
所以模拟即可。
考试时还是要大胆猜想，小心求证。猜结论算是信息学竞赛特有的了。

B

0.前缀和：\(\large sa_i = \sum\limits_{j=1}^{i} a_j\) 。
1.贡献思想，考虑分析一个\(b_i\)会和哪些a乘起来，然后就有式子：
\(\large \sum\limits_{i=1}^{n}b_i\sum\limits_{l=1}^{i}\sum\limits_{r=i}^{n}(sa_r - sa_{l-1})\)
2.继续贡献思想，考虑分析一个sa会被正着和反着算几次：
\(\space \space \space \space \space \large \sum\limits_{i=1}^{n}b_i(i\cdot\sum\limits_{j=i}^{n}sa_j - (n-i+1)\cdot\sum\limits_{j=0}^{i-1}sa_j) \\\)
\(\large =\sum\limits_{i=1}^{n}b_i(i\cdot(ssa_n - ssa_{i-1}) - (n-i+1)ssa_{i-1})\)
3.现在继续前缀和：\(\large sssa_i = \sum\limits_{j=1}^{i}(j\cdot(ssa_n - ssa_{j-1}) - (n-j+1)ssa_{j-1})\)
初始时\(\large ans = \sum\limits_{i=1}^{n}b_i(sssa_i - sssa_{i-1})\)
4.对于修改，ans加上\(\large k(sssa_r - sssa_{l-1})\)即可。

C

首先我们发现这个期望其实是假的。
1.我们分析一下，在全排列中，\(i\)和\(j\)两个点相邻的方案数：
自己内部2种，放置的位置\(m-1\)种，其他的点乱放\((m-2)!\)种。
所以\(\large ans = \frac{2\sum dis(a_i，a_j)}{m}\)，阶乘约了。
2.对于关键点距离和，我们换根应该是好求的。
3.考虑修改怎么做。我们只需要考虑，一个点的连接的每一条边会被经过几次即可。这个也是容易的。具体地，可以先记录每个点连向父亲的边被经过了几次，然后每个点再扫一遍儿子求和，否则容易被菊花图卡。

D

很少有能改到D的场啊。
1.我们考虑根号分治。对于模数\(\large x \le \sqrt{n}\)的，就考虑搞一个\(s_{x,i}\)代表膜x为i的数的增量和。然后前缀和，\(\large ss_{x,i} = \sum\limits_{j=0}^{i-1}s_{x,i}\)，修改是简单的。查询的话，有点难办，自己手玩一下吧。
2.对于模数大于根号的也有办法，用分块搞一个\(O(1)\)区间修改，\(O(\sqrt{n})\)区间查询的东西就行了。具体地，我们先差分，\(\large c_i = a_i - a_{i-1}\)。
3.查询经过了一些转化，就是\(\big (r-l+1)\sum\limits_{i=1}^{l-1}c_i + (r+1)\sum\limits_{i=l}^{r}c_i - \sum\limits_{i=l}^{r}i \cdot c_i\)。所以整块维护一个sum1和sum2即可。修改的话，sum1容易的，sum2也差不多，就是把区间修改转化成单点修改。

周三

打的还行，改题改得太几把烂了。

A

结论是显然的，long long是没有开的。
容易发现，奇数位置和偶数位置互不影响。然后一次交换会减少3个逆序对。所以我们考虑：
1.先判断是不是奇数位置上都是奇数，偶数位置上都是偶数。
2.再判断总的逆序对个数是不是等于(奇数序列逆序对个数+偶数序列逆序对个数)*3。

周四

做了一些专题的题，但是都是简单题。
数据结构专题D是原，A就是考虑它实际上是一个二维偏序，先把询问离线按右端点排序，把每个点的\(i-L_i\)存到线段树下标为\(L_i\)的地方，这样就可以维护两维的偏序关系。

周六

打得还不错，主要是因为打出来了D的40pts部分分，所以排名上看着还行。

A

事实上是弱智题，但是乍一看题解容易感觉题解是伪的。
1.我们考虑把第一次修改的点当作根。
2.维护下面所有开启了投票装置的点到根的答案。
3.查询时查询从u直接走到rt的路径上的最小值，和2维护的答案的min就行，因为根已经开启了，我可以直接走到根，或者在LCA处转向。

B

一个比较经典且重要的题。
1.首先考虑不换根怎么做，就是用树形DP check每个点当根行不行。
2.设\(g_u\)为以u为根的子树中，所有的关键点到根的距离和，\(f_u\)为\(g_u\)在经过一系列操作后，所能达到的最小值，\(sz_u\)为子树里面关键点个数。
3.考虑f的计算。我们枚举每一棵子树\(v\)，如果对于每个v都有\(\large f_v + sz_v \le g_u -g_v - sz_v\)，那么就可以把这棵子树里面的一直往上跳，此时\(f_u\)就是\(g_u\)的奇偶性。
4.如果有一个\(\large f_v + sz_v > g_u -g_v - sz_v\)那么只能有一个这样的v，\(\large f_u = f_v + sz_v - g_u + g_v + sz_v\)。如果最后\(f_rt == 0\)那么答案就是g的一半，否则不能取答案。
5.考虑换根怎么做。我们每次其实只需要知道对于每一个v的\(\large f_v + g_v + 2 * sz_v\)即可，考虑放进set里面维护。
6.我们可以容易地根据当前set的情况，计算出来\(f_u\)，set的维护的话，就是每次把一个子树换到根上面，修改完数据，再换下去即可。

周日

感觉这场是sb场啊，不是很想总结，打得也非常垃圾。

A

我们需要一个修改\(O(1)\)，查询\(O(\log n)\)的算法。
考虑反向使用ST表。就是修改时给两大块打上标记，查询的时候就是把这些标记下放下去，一整遍是\(O(n\log n)\)的。

B

一个线性基相关的题，改了但是不想总结。

第三周

周一

这场打得不咋样，但是比较有总结价值。T1差一点就做出来了啊。

A

先前缀和一下，原式变为：
\(\large \sum\limits_{i=1}^{n} \sum\limits_{j=i}^{n} (a_j \oplus a_{i-1}) ^ 2\)
考虑按位分析。
\(\large \sum\limits_{i=1}^{n} \sum\limits_{j=i}^{n} (\sum\limits_{k=0}^{20}a_{j,k} \neq a_{i-1,k}乘上位值) ^ 2\)
考虑拆平方，首先是会有一些自己的二次方项。
可以设\(s_{k,0/1}\)为j前面的数之中所有第k位为0/1的贡献和，然后我们枚举\(a_j\)的二进制位即可知道前面在这一个位上和自己不同的贡献了。
贡献每次累加\(\large 2^{2k}\)即可。

接下来考虑形如\(2ab\)的项。
设\(ss_{k,l,0/1,0/1}\)就是前面第k位为0/1且第l位为0/1的贡献和。然后处理方式其实和上面的差不多了。

B

需要使用set。先咕了。

周二

T1弱智了，方案多输出了空格，100->0。

A

按照大样例给出的方法，稍加构造即可得出答案。

B

考虑二分老师期望能抓到多少人。我们要看学生能不能使得期望\(\le mid\)。
那么就只有人数大于mid的教室需要布防，这样的教室如果同学进入的概率是\(p_i\)，那么老师期望抓到的人数就是\((1-p_i) \times a_i \le mid\)。这样可以算出来每一个p的下界，含义就是我至少得给i分配下界的概率，才能够保全期望。
所以如果这个下界加起来超过1了，说明mid算小了。否则mid算大了。我们随之记录答案即可。