习惯孤独 题解

我们发现：
1.k非常小。
2.每一刀是独立的。每次要切掉的大小是\(a_{i-1} - a_i\)。
于是选择状压DP。

我们设\(f_{u, sta}\)为以u为根的子树，目前已经完成了sta状态中所标示为1的切的方案数。
考虑这么一个图（抽象派）：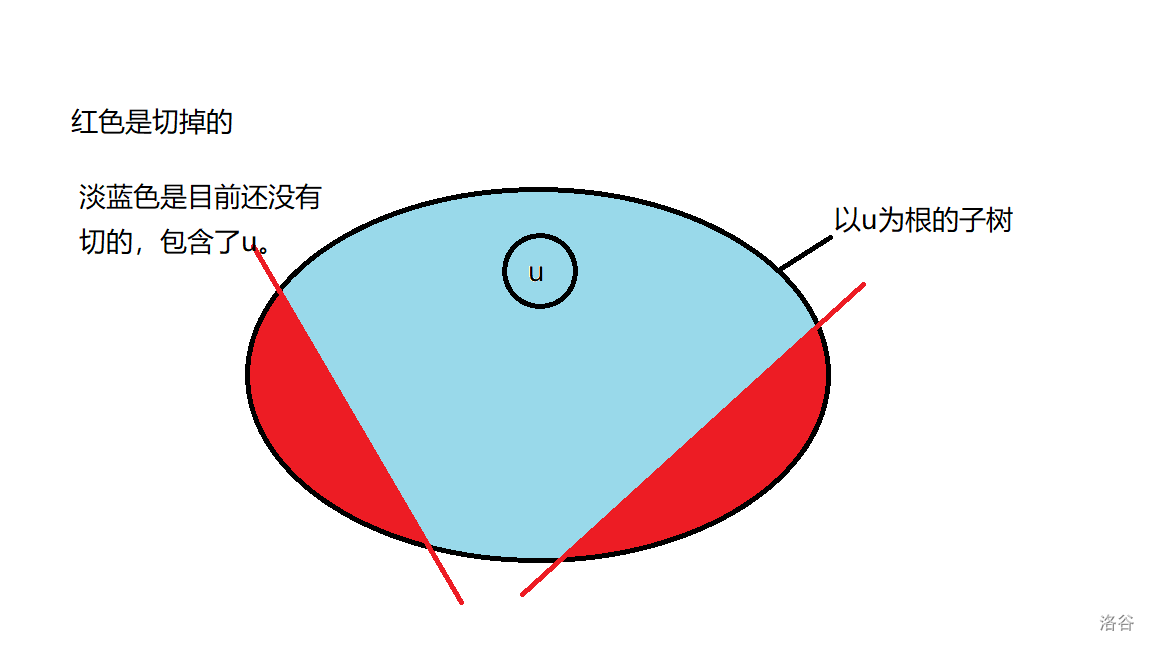

然后转移就分两步：
1.把子树或起来：\(f_{u,sta1 | sta2} += f_{son1, sta1} \times f_{son2, sta2}\)，注意sta1和sta2不能有共同的都切过了的刀，即\(sta1 \& sta2 == 0\)。注意此时记录一个g=f，这个g数组代表不包含u的以u为根的子树的方案数。

2.选择还没有切的刀，把它切掉：\(f_{u, sta | (1 << i)} += g_{u, sta}\)，注意此时要求的是：上图中淡蓝色联通块大小等于这一刀要切的大小，就是把u和u的父亲的链接斩断了。

好的到这里dfs1就结束了。

好的接下来维护一个前缀和和后缀和，\(pre[i][j]\)就是u的前i个子树，切除状态为j的方案数之和；然后\(suf[i][j]\)就是第i个子树到最后一个子树，切除状态为j的方案数之和。备注：其实不是“和”，而是方案数的合并，就是按照求解f的方式把pre和f合并，得到新的f；suf同理。

接下来是重头戏：求解h。\(h_{u,sta}\)代表以u为根的子树外的方案数。
然后先不考虑如何求解h，思考由上面定义的数组如何计算答案。结果是\(\sum_{i = 1}^{n} g_{i, sta1} \times h_{i, sta2}\)，还是注意两个sta与起来是0。

然后还要除以一个\(a_k\)，原理是我们在计数时，钦定u是要属于最后一个联通块的，所以既不能把它的贡献算到子树里，也不能算到父亲一坨里。 这样每个块里面，会有\(a_k\)个点记录同一种方案，所以要除掉。

现在再考虑h怎么算。分三个部分：
1.来自u的兄弟，就是要把刚才求的pre和suf合并起来。
2.来自u的父亲，就是把父亲的和自己的h合并起来。
3.来自切割掉这一坨上要切割的后，发现这个块的大小刚好是一次切割要求的，就像求f的时候一样求一下。

到这里本题算法流程结束，总结一下，就是将一个节点钦定在最后一个联通块里面，然后计算其他节点的方法，最后合并，并且使用状压DP。