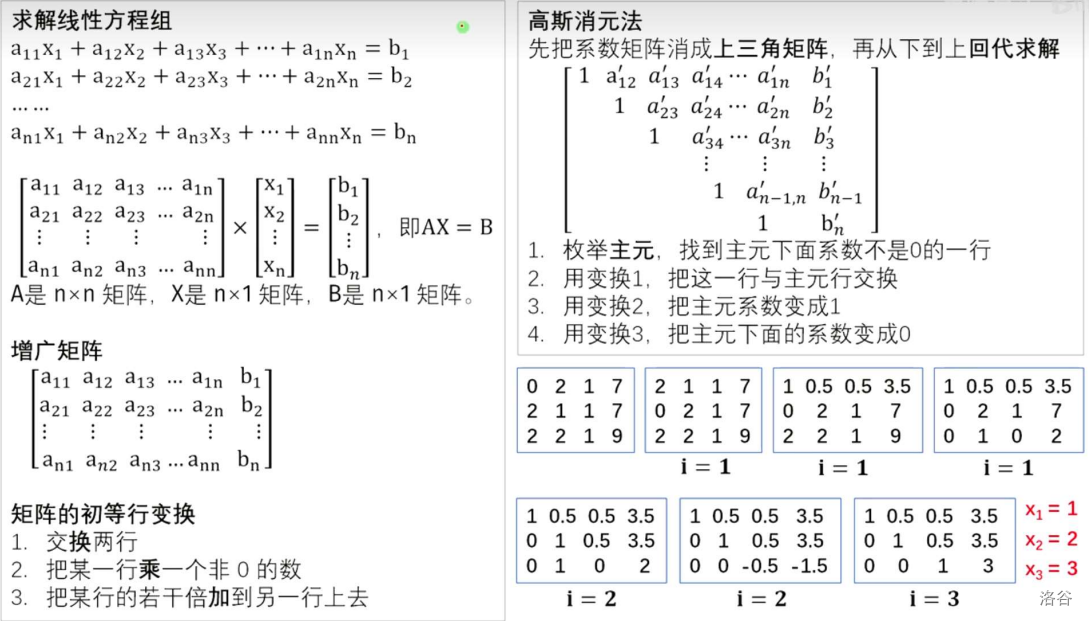
高斯消元

因为写概期用到了，所以回来复习一下。

先放置一张图，然后放一个满是注释的代码。

int guass()
{
	int r;
	for(int i = 1; i <= n; i++)
	{
		r = i;
		for(int j = i + 1; j <= n; j++)
			if(fabs(a[j][i]) > eps){r = j; break;}
		if(fabs(a[r][i]) < eps)return 0;
		if(i != r)swap(a[i], a[r]);
		//这一部分是寻找i下面主元系数不为0的一行，换上来 
		double x = a[i][i];//主元系数 
		for(int j = i; j <= n + 1; j++)a[i][j] /= x;//主元系数化为1 
		for(int k = i + 1; k <= n; k++)//只需要考虑i下面的行 
		{
			x = a[k][i];//这一行中主元的系数，要进行加减消元 
			for(int j = i; j <= n + 1; j++)a[k][j] -= x * a[i][j];//加减消元 
		}
	}
	for(int i = n - 1; i >= 1; i--)//回带未知数的值 
		for(int j = i + 1; j <= n; j++)//要和下面一行对齐
			a[i][n + 1] -= a[i][j] * a[j][n + 1];//数值减去下面未知数的值乘上本行该未知数的系数 
	 
    //往下的一部分是判无解的 
	int flag = 1;
	for(int i = 1; i <= n; i++)
	{
		if(fabs(a[i][i]) < eps)
		{
			if(fabs(a[i][n + 1]) >= eps)flag = -1;//有0x == a(a != 0)，显然无解 
			else if(flag != -1)flag = 0;//有0x == 0，无数种解 
		} 
	}
	return flag;
}

需要记住一个事情：消元从上到下，回代从下到上。