卷积神经网络

基本组件

卷积

相乘，再求和。

\[C_{x,y} = \sum A_{i,j,k} \times B_{i,j,k} \]

• 有几个卷积核，输出通道数就是几。

一维卷积

二维卷积

参见：

• Convolutions Over Volume | Coursera

• But what is a convolution? | 3Blue1Brown

• CNN Explainer

转置卷积

\[A_{i,j,k} = C_{x,y} \times B_{i,j,k} \]

参见：Transpose Convolutions | Coursera

应用

目标检测

概述

• 目标识别：识别图像中物体的类别（图片中有人还是狗）
• 目标定位：识别图像中物体的位置（图片中人的位置在哪里）
• 目标检测：识别图像的类别并定位（识别图片中的人和狗以及它们的位置）

目标检测的经典算法是 YOLO（You Only Look Once）。

基本流程

输入精确切割的目标图像，输出目标的类别。

卷积实现的全连接层：

用一个和输入张量同尺寸的卷积核可以实现全连接层的功能。

滑动窗口检测算法

不断对窗口运行目标识别算法，即可获得每个位置的识别结果。

对窗口内的图像运行图像识别算法：

其实可以对全图使用卷积运行一次图像识别，即可得到各个区域的结果：

在设计训练集时，可以计算每个物体的中心位置 \((b_x, b_y)\)，并分配给唯一的窗口。对于这个窗口，其标签为 \((p_c, b_x, b_y, b_h, b_w, c_1, c_2, c_3)\)。其中，\(p_c\) 表示窗口是否有物体，\((b_h, b_w)\) 表示物体边框的高和宽，\((c_1, c_2, c_3)\) 表示物体的具体类别。

\(b_x, b_y \in [0, 1]\)，是相对位置。\(b_h, b_w \geq 0\)，是相对长度。

参考：Convolutional Implementation of Sliding Windows | Coursera

原始论文：You Only Look Once: Unified, Real-Time Object Detection

语义分割

语义分割在目标检测之上更进一步，将目标的轮廓绘制出来。常见的应用如自动驾驶，病灶识别。

语义分割的经典算法是 U-Net。

与 YOLO 不同，U-Net 的后几层通过转置卷积增大张量尺寸到图像尺寸，并为每个像素分类。

简单理解，U-Net 是将 YOLO 后几层替换成转置卷积（Transpose Convolution）层的结果。

实际上 U-Net 的结构如下：

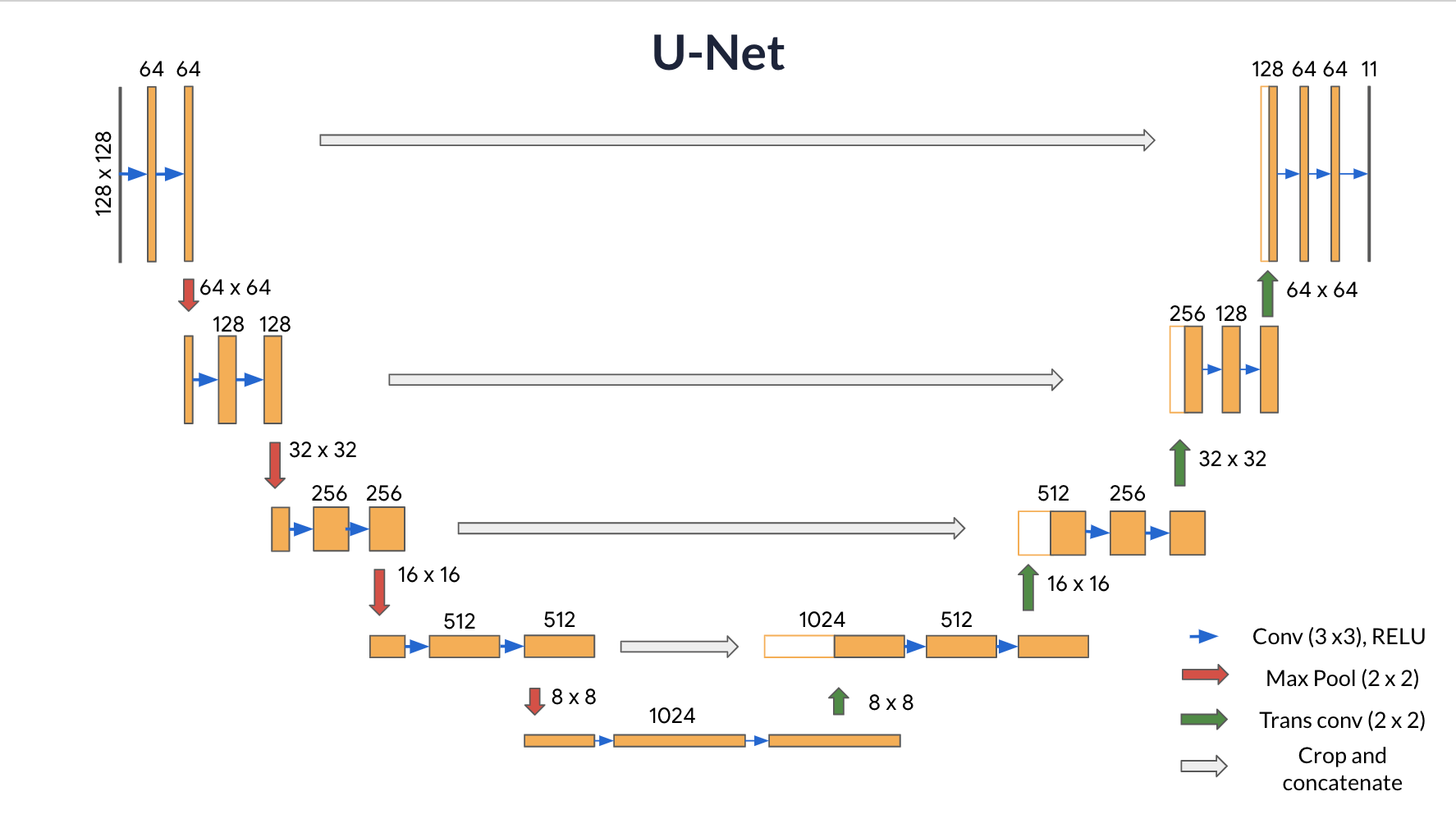
参考：U-Net Architecture | Coursera

原始论文：U-Net: Convolutional Networks for Biomedical Image Segmentation

人脸识别

孪生网络（Siamese Network）：

可以定义样本距离 \(d(x^{(1)}, x^{(2)})\)：

\[d(x^{(1)}, x^{(2)}) = \left\| f(x^{(1)}) - f(x^{(2)}) \right\|_2^2 \]

\(\|\cdot\|_2\) 表示 欧几里得范数

参考：Siamese Network | Coursera

三元损失（Triplet Loss）：

\[J(A, P, N) = \sum_{i=1}^m \left[ \left\| f(A^{(i)}) - f(P^{(i)}) \right\|_2^2 - \left\| f(A^{(i)}) - f(N^{(i)}) \right\|_2^2 + \alpha \right]_+ \]

• \(A\)：Ahchor，某人的图片。\(P\)：Positive，同人图。\(N\)：Negative，不同人图。
• 设置 \(\alpha\) 是为了避免网络将所有 \(f(x)\) 置零从而逃避学习数据特征。

参考：Triplet Loss | Coursera

定义为分类问题：

\[\hat y = \sigma\left(\sum_k \left\| f(x^{(i)})_k - f(x^{(j)})_k \right\| \right) \]

参考：Face Verification and Binary Classification | Coursera

风格迁移

风格迁移生成图像的方式是，先生成一张随机噪声图，然后计算图像的代价并运行梯度下降。也就是说，生成图像的过程是一个训练过程，只不过训练得到的不是模型而是图像。

将内容图像 \(C\) 和风格图像 \(S\) 分别输入到预训练的 CNN 网络，以获得网络各层的激活值 \(a^{[l](C)}\) 和 \(a^{[l](S)}\)。

代价函数

生成图像 \(G\) 的代价函数 \(J(G)\)：

\[J(G) = \alpha J_{\text{content}}(C, G) + \beta J_{\text{style}}(S, G) \]

其中，\(\alpha + \beta = 1\)。

参考：Cost Function | Coursera

内容代价

内容代价 \(J_{\text{content}}(C, G)\)，衡量生成图像和原始图像的相似度：

\[J_{\text{content}}(C, G) = \frac{1}{2 n_H n_W n_C} \sum \left\| a^{[l](C)} - a^{[l](G)} \right\|_F^2 \]

参考：Content Cost Function | Coursera

风格代价

通道之间的相关度就是风格。由此我们可以定义风格矩阵 \(G\)（Gram matrix），其记录了通道间的相关度：

\[G = A^{\top} A \]

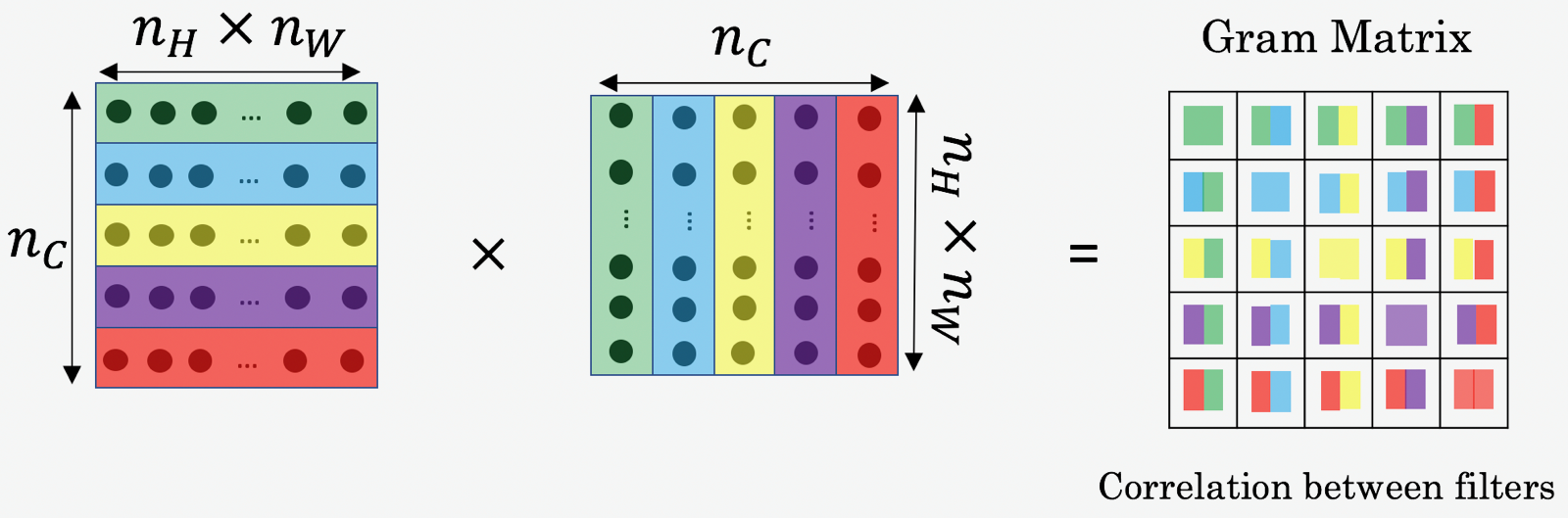
风格图像的风格 \(G_{kk'}^{[l](S)}\)：

\[G_{kk'}^{[l](S)} = a_k^{[l](S)} a_{k'}^{[l](S)} \]

生成图像的风格 \(G_{kk'}^{[l](G)}\)：

\[G_{kk'}^{[l](G)} = a_k^{[l](G)} a_{k'}^{[l](G)} \]

第 \(l\) 层的风格代价 \(J_{\text{style}}^{[l]}(S, G)\)：

\[\begin{aligned} J_{\text{style}}^{[l]}(S, G) &= \frac{1}{\ldots} \left\| G^{[l](S)} - G^{[l](G)} \right\|_F^2 \\ &= \frac{1}{\left( 2 n_H^{[l]} n_W^{[l]} n_C^{[l]} \right)^2} \sum_k\sum_{k'} \left(G_{kk'}^{[l](S)} - G_{kk'}^{[l](G)}\right)^2 \end{aligned} \]

\(\|\cdot\|_F\) 表示 Frobenius 范数

风格代价 \(J(S, G)\)，衡量生成图像和风格图像的相似度：

\[J_{\text{style}}(S, G) = \sum_l \lambda^{[l]} J_{\text{style}}^{[l]}(S, G) \]

参考：Style Cost Function | Coursera