CF1870B Friendly Arrays 题解

前言

这是一道大水题但我还是想了很久，主要考查选手对于位运算的理解。

正文

题目大意

已知有一个长度为 $n$ 的序列 $a$ 和一个长度为 $m$ 的序列 $b$，现在你可以选取任意的一个 $b_j$ 满足 $1\leq j\leq m$，并把所有的满足 $1\leq i\leq n$ 的 $a_i$ 和 $b_j$ 做按位或运算。已知变量 $x=a_1 \oplus a_2 \oplus \dots \oplus a_n$，请分别求出 $x$ 的最小值和最大值。

解题思路

我们可以把 $a$ 数组转化成二进制后近似的看作一个二维数组。易证，对于每一个 $b$ 数组中的元素，该元素可以把与它每一位相对应的且元素该位为 $1$ 的 $a_i$ 的这一位全部转化为 $1$，如下图所示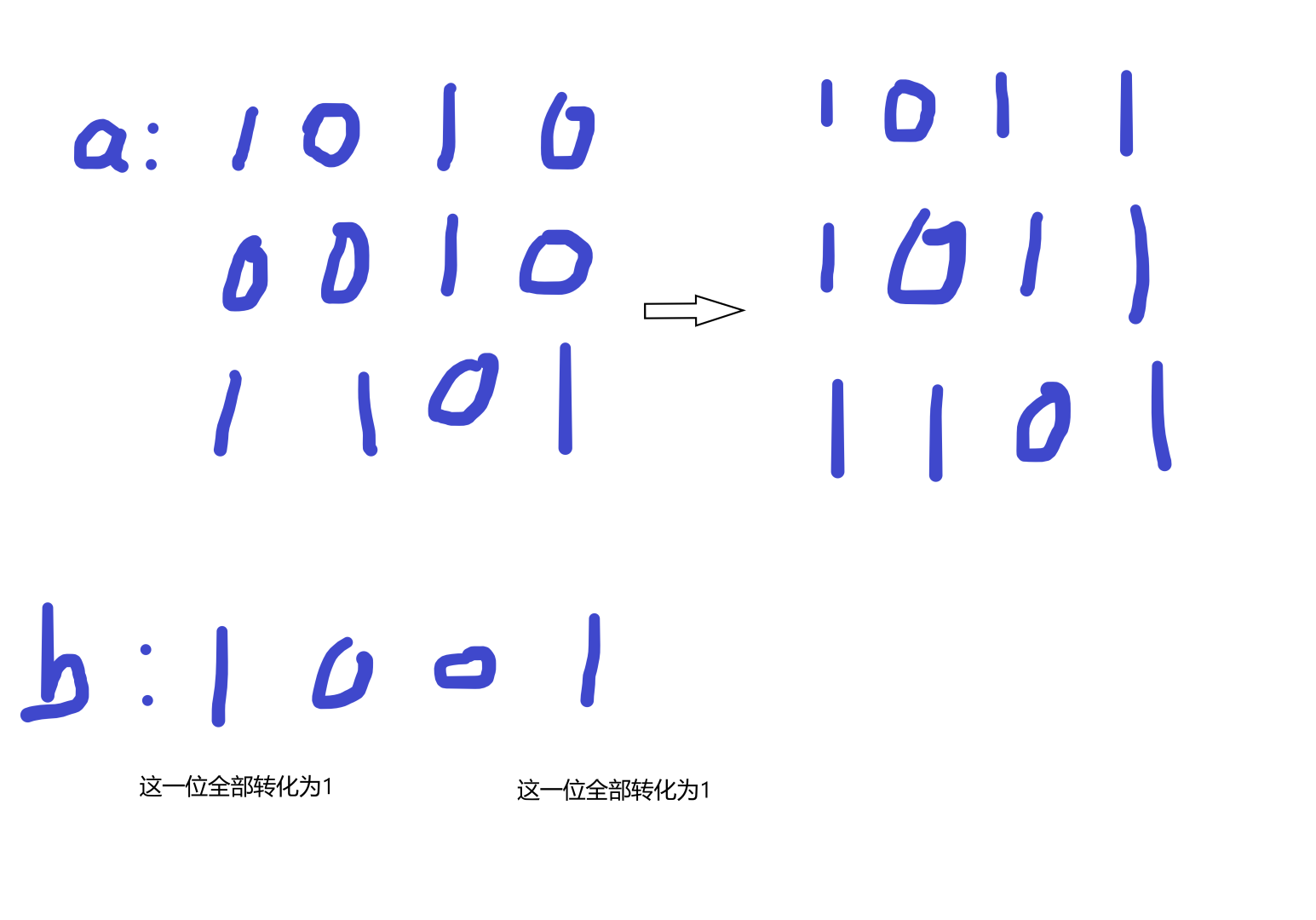： 由此可以知道，对于 $n$ 为偶数的 $a$ 数组，其 $x$ 的最大值为原本数组中所有元素的异或和，最小值为数组中的元素对于 $b$ 数组中的所有元素的按位或运算之和的按位或的值的异或和；同理，当 $n$ 为奇数时，最大值为运算后的异或和，最小值为原来的元素的异或和。

AC代码

#include<bits/stdc++.h>
using namespace std;
inline char gc() {
    static char buf[1 << 14], * p1 = buf, * p2 = buf;
    return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 14, stdin), p1 == p2) ? EOF : *p1++;
}
inline void read(int& x) {
    x = 0; int f = 1; char ch = getchar();
    while (ch < '0' || ch>'9') { if (ch == '-') f = -f; ch = getchar(); }
    while (ch >= '0' && ch <= '9') { x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar(); }
    x = (f == -1 ? -x : x); return;
}
inline void put(int x) {
    if (x < 0) putchar('-'), x = -x;
    if (x > 9) put(x / 10);
    putchar(x % 10 + '0'); return;
}inline void write(int x) { put(x); putchar('\n'); }
#define N 200005
int n,m,ans,mint,maxt;
int a[N],b[N];
inline void work(){
    read(n),read(m);
    for(int i=1;i<=n;i++)
        read(a[i]);
    for(int i=1;i<=m;i++)
        read(b[i]);
        maxt=a[1];
    for(int i=2;i<=n;i++){
        maxt^=a[i];
    }mint=maxt;
    if(n%2==0){
        int huo=0;
        for(int i=1;i<=m;i++)
            huo|=b[i];
        mint=(a[1]|huo);
        for(int i=2;i<=n;i++){
            mint^=(a[i]|huo);
        }
    }else{
        int huo=0;
        for(int i=1;i<=m;i++){
            huo|=b[i];
        }maxt=a[1]|huo;
        for(int i=2;i<=n;i++){
            maxt^=a[i]|huo;
        }
    }
    put(mint),putchar(' '),write(maxt);
}
int main() {
    int T;read(T);
    while(T--) work();
    return 0;
}