P4005 小 Y 和地铁 题解

解题思路

一眼丁真，模拟退火，那么具体怎么做呢，先来看看我们已经知道的结论：

1. 因为每条线路与所乘坐的线路最多只有两个换乘点，因此可以知道，这些线路可以看作若干条曲线线段，由此，我们可以把题意转化一下：

   • 已知有 $n$ 条曲线与一条直线相交，这些曲线和直线没有重合的部分且交点处只有两条线，不存在封闭曲线，求这些曲线之间的交点的最小值。

   由此可得，我们可以先把这 $n$ 个点处理一下，得到剩下的 $m$ 个点，这 $m$ 个点中，每个点均出现了两次（也就是说删除只出现了一次的点）。

2. 我们可以推出，所有的曲线共有 $6$ 种状态：

   • 全部位于线段下方；

   • 全部位于线段上放；

   • 从线段左端点到当前曲线左端点位于线段下方，从左端点到当前曲线右端点位于线段上方，可以看做将当前曲线分成了从线段左端点到曲线左端点的一条位于线段下方曲线和从左端点到曲线右端点的一条位于线段上方的曲线，如图：

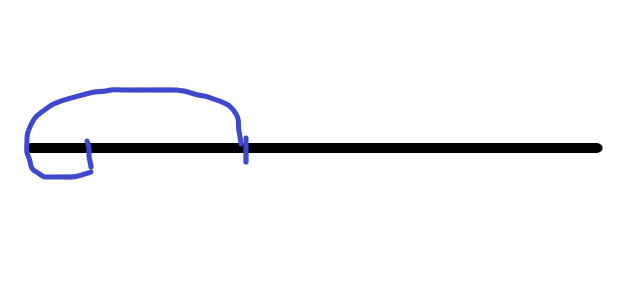
   • 从线段左端点到当前曲线左端点位于线段上方，从左端点到当前曲线右端点位于线段下方，可以看做将当前曲线分成了从线段左端点到曲线左端点的一条位于线段上方曲线和从左端点到曲线右端点的一条位于线段下方的曲线，如图：

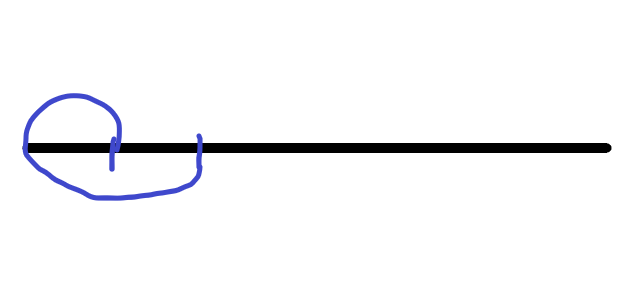
   • 从线段右端点到当前曲线右端点位于线段下方，从右端点到当前曲线的右端点位于线段上方，可以看做将当前曲线分成了从线段右端点到曲线右端点的一条位于线段下方曲线和从右端点到曲线左端点的一条位于线段上方的曲线，如图：

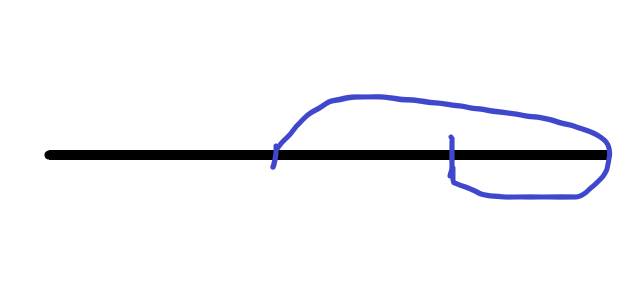
   • 从线段右端点到当前曲线右端点位于线段上方，从右端点到当前曲线的右端点位于线段下方，可以看做将当前曲线分成了从线段右端点到曲线右端点的一条位于线段上方曲线和从右端点到曲线左端点的一条位于线段下方的曲线，如图：

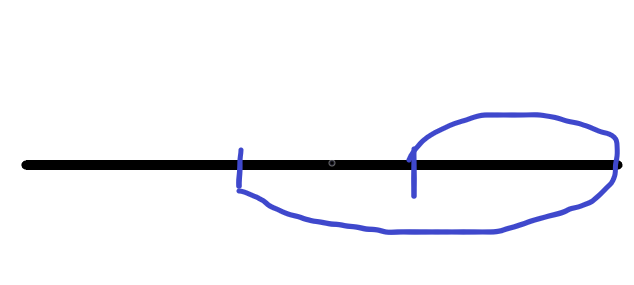
3. 两条曲线 $x$ 和 $y$ 有交点，当且仅当 $x.first<y.first<x.second<y.second$ 或 $y.first<x.first<y.second<x.second$ 且 $x$ 和 $y$ 位于同一方向。

做法如下：

1. 考虑维护一个关于曲线的集合，每一条曲线的表示如下：

   • stu：表示当前曲线的状态；

   • cnt：表示当前的曲线可以拆分为几条曲线，值为 $1$ 或 $2$；

   • line[]：表示当前曲线是由那几条曲线组合成的，其中，line 为一个 pair 类型的数组，最多可以存放两个元素，line 的 first 值表示曲线的左端点，second 表示曲线的右端点。

2. 考虑预处理出每条曲线最开始的状态，然后每次随机修改一条曲线的状态，不难发现，单次修改第 $i$ 条线段对于交点个数的影响为 $\displaystyle \Delta=\sum_{j=1}^{m} D(i_{lst},j)-\sum_{j=1}^{m} D(i_{now},j)$，其中 $\Delta$ 表示交点减少的数量，$D(i,j)$ 表示第 $i$ 条曲线和第 $j$ 条曲线交点的数量，$i_{lst}$ 表示修改前的第 $i$ 条曲线 $i_{now}$ 表示修改后的第 $i$ 条曲线，那么我们新的答案 $nowans=lstans-\Delta$，如果是最优解，直接更新答案，否则以一定概率接受，如果没有接受，那么需要改回第 $i$ 条曲线，消除随机修改的影响。

时间复杂度分析

我们预处理答案是 $O(n^2)$ 的，而单次修改答案的时间复杂度不会超过 $O(2n)$，那么总时间复杂度即为 $\displaystyle O\left(C\times 2n\log_{\Delta T} \frac{T_0}{T_e}\right)$，其中 $\Delta_T$ 为降温系数，$T_0$ 为初温，$T_e$ 为末温，$C$ 为模拟退火的次数，时间复杂度是能过的。当然了，本题肯定是有更优的更新方法的，可惜这里空白太小写不下。