Learn Learn Crypto
参考文章(多数都是搬这个老登的): https://www.cnblogs.com/gaoyucan/p/17087521.html
流密码
常见的有 RC4、Salsa20 以及 ChaCha20.之前一直是识别加密算法,虽然只会识别一个rc4,遇到其他还是傻眼,一直没想到流密码的密文是仅由明文与密钥流异或得到的,以此识别出流密码后,动调获取密钥流或者将密文patch进去拿输出即可.(明明就在高神的流密码第一段,这么久了才发现)
RC4
/*初始化函数*/
void rc4_init(unsigned char *s, unsigned char *key, unsigned long Len) {
int i = 0, j = 0;
char k[256] = {0};
unsigned char tmp = 0;
for (i = 0; i < 256; i++) {
s[i] = i;
k[i] = key[i % Len];
}
for (i = 0; i < 256; i++) {
j = (j + s[i] + k[i]) % 256;
tmp = s[i];
s[i] = s[j]; // 交换s[i]和s[j]
s[j] = tmp;
}
}
/*加解密*/
void rc4_crypt(unsigned char *s, unsigned char *Data, unsigned long Len) {
int i = 0, j = 0, t = 0;
unsigned long k = 0;
unsigned char tmp;
for (k = 0; k < Len; k++) {
i = (i + 1) % 256;
j = (j + s[i]) % 256;
tmp = s[i];
s[i] = s[j]; // 交换s[x]和s[y]
s[j] = tmp;
t = (s[i] + s[j]) % 256;
Data[k] ^= s[t];
}
}
Salsa20
遇到的话,有时间就补
ChaCha20
同上,暂时记一下例题[RCTF2022 checkserver],顺便附一个识别图,感觉好像见过
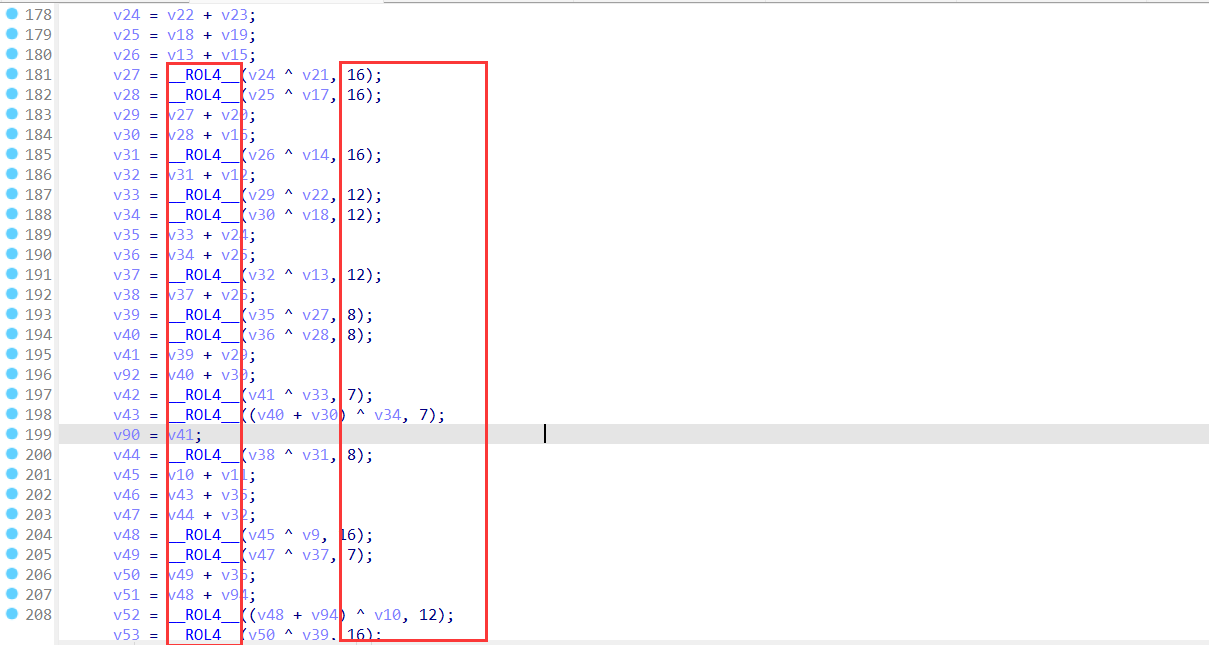
分组加密
Tea
#include
void encrypt (uint32_t* v, uint32_t* k) {
uint32_t v0=v[0], v1=v[1], sum=0, i; /* set up */
uint32_t delta=0x9e3779b9; /* a key schedule constant */
uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */
for (i=0; i < 32; i++) { /* basic cycle start */
sum += delta;
v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
} /* end cycle */
v[0]=v0; v[1]=v1;
}
void decrypt (uint32_t* v, uint32_t* k) {
uint32_t v0=v[0], v1=v[1], sum=0xC6EF3720, i; /* set up */
uint32_t delta=0x9e3779b9; /* a key schedule constant */
uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */
for (i=0; i<32; i++) { /* basic cycle start */
v1 -= ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
v0 -= ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
sum -= delta;
} /* end cycle */
v[0]=v0; v[1]=v1;
}
Tea类加密很好识别,delta=0x9e3779b9会被魔改
XTea
#include
/* take 64 bits of data in v[0] and v[1] and 128 bits of key[0] - key[3] */
void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
unsigned int i;
uint32_t v0=v[0], v1=v[1], sum=0, delta=0x9E3779B9;
for (i=0; i < num_rounds; i++) {
v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
sum += delta;
v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
}
v[0]=v0; v[1]=v1;
}
void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
unsigned int i;
uint32_t v0=v[0], v1=v[1], delta=0x9E3779B9, sum=delta*num_rounds;
for (i=0; i < num_rounds; i++) {
v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
sum -= delta;
v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
}
v[0]=v0; v[1]=v1;
}
与tea区别sum+=delta位置,key[(sum>>11) & 3]与key[sum & 3],其中detal会被魔改,移位数可能被魔改
XXTea
#define DELTA 0x9e3779b9
#define MX ((z>>5^y<<2) + (y>>3^z<<4) ^ (sum^y) + (k[p&3^e]^z))
long btea(long* v, long n, long* k) {
unsigned long z=v[n-1], y=v[0], sum=0, e;
long p, q ;
if (n > 1) { /* Coding Part */
q = 6 + 52/n;
while (q-- > 0) {
sum += DELTA;
e = (sum >> 2) & 3;
for (p=0; p<n-1; p++) y = v[p+1], z = v[p] += MX;
y = v[0];
z = v[n-1] += MX;
}
return 0 ;
} else if (n < -1) { /* Decoding Part */
n = -n;
q = 6 + 52/n;
sum = q*DELTA ;
while (sum != 0) {
e = (sum >> 2) & 3;
for (p=n-1; p>0; p--) z = v[p-1], y = v[p] -= MX;
z = v[n-1];
y = v[0] -= MX;
sum -= DELTA;
}
return 0;
}
return 1;
}
一般来说,识别可以通过,delta 以及round = 6 + 52/n、(sum >> 2) & 3这种特殊的运算来判断。
这里v指密文或者明文:n指round[len(flag)/4]正是加密,负是解密:k指密钥
魔改点:
- (sum>> 2) & 3改为(sum >> 2)& 5,注意此时的密钥变成了6*4字节(6个整型)

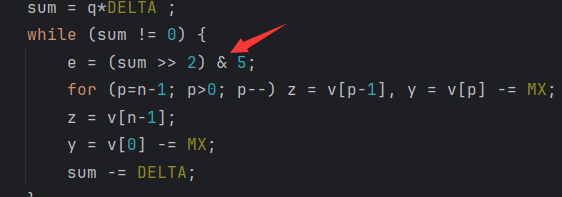
- delta值
- MX函数(z>>5^y<<2) + (y>>3^z<<4)中间的左移右移位数修改
- 最基础的就是将long类型转为uint32_t,注意改解密脚本的时候别把n的long类型也改了
DES
DES的密钥位64bit,但每个字节的第八位(最后一位)是奇偶校验位,所以有效密钥为56bit
主要通过 S盒 以及各个置乱表来识别,可以使用插件来自动化识别这些特征。
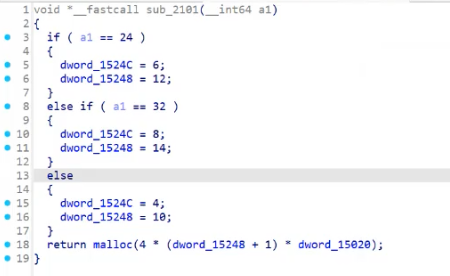
AES
AES(Advanced Encryption Standard,高级加密标准),分组大小为128位,根据密钥长度和轮数可以分为 AES-128、AES-192、AES-256,具体区别如下表:
| AES-128 | AES-192 | AES-256 | |
|---|---|---|---|
| 密钥长度 | 128 | 192 | 256 |
| 轮数 | 10 | 12 | 14 |
对于如何识别是哪一种,可能看密钥大小不好观察,可以选择看循环的次数
整体流程
整体来说AES加密有如下几步
- 密钥拓展,使用密钥拓展算法通过初始密钥获取轮密钥
- AES使用一个密钥扩展算法将原始密钥生成多个轮密钥(Round Keys),这些轮密钥在后续的加密轮次中使用。对于128位密钥,会生成10轮密钥
- 初始轮密钥加
- 将明文数据(明文)与第一个轮密钥进行异或(XOR)运算,得到初始状态。
- 主加密轮
- S盒替换(SubBytes)
- 行移位(ShiftRows)
- 列混合(MixColumns)
- 轮密钥加(AddRoundKey)
- 最后一轮(与主加密轮类似,但省略列混合)
- S盒替换(SubBytes)
- 行移位(ShiftRows)
- 轮密钥加(AddRoundKey)
解密
from Crypto.Cipher import AES
import struct
key = struct.pack("<4Q", 0xaaaaaaaaaaaaaaaa, 0xaaaaaaaaaaaaaaaa, 0xaaaaaaaaaaaaaaaa, 0xaaaaaaaaaaaaaaaa)
cipher = b"aaaaaaaaaaaaaaa"
aes1 = AES.new(key, mode=AES.MODE_ECB)
aes2 = AES.new(key, mode=AES.MODE_CBC, iv=b"")
flag = aes1.decrypt(cipher)
print(flag)
白盒AES
2022年国赛分区赛逆向有个,解法可以参考下面的文章:
https://bbs.pediy.com/thread-254042.htm
- 白盒AES介绍:白盒AES将S盒,轮密钥加,(行移位)?结合在一起形成了一个big box,进而起到防止攻击者得到密钥与轮密钥的作用.
- 差分故障分析:第十轮无列混淆,.在第九轮列混淆前注入,修改一个字节,输出密文会有几个字节的差别.
- 得到step2中的结构后,使用phoenixaes,第一行传入正确密文,后面传入故障密文,并且phoenixaes会检测故障密文是否合规
- 错误密文为4个字节: good candidate
- 错误密文大于4个字节: too much impact
- 错误密文小于4个字节: too few impact
- 经过step4后会得到k10,此时可使用stark中的aes_keyschedule
.\aes_keyschedule.exe D014F9A8C9EE2589E13F0CC8B6630CA6
识别
-
密钥字节数对应轮数
-
插件识别
-
AES查表法识别
-
(Te0,Te1,Te2,Te3)例Te0:
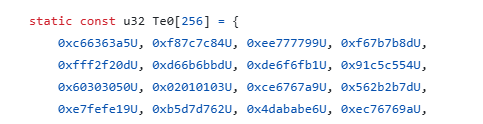
-
很多异或:

-
魔改
- 在某一步实现的函数里面加一个可逆的运算(一般是异或).
- 将行移位与列混合的顺序调换一下.
- S盒代换中将S盒修改一下
- 密钥拓展被修改,不进行分析哪里修改,直接动调将生成的轮密钥dump下来,之后对着源码,将密钥拓展函数(static void KeyExpansion())过程注释,将dump下来的轮密钥直接赋值给RoundKey
- (不知道会不会出,学习的时候想到的这个点)魔改Te表
解决方法:Te表中的每一个元素的中间两字节相同,且都是sbox的元素(魔改的sbox一样适用)

- 注意在分析魔改点的时候,需要注意ida与tiny-aes的行列优先关系
SM4
SM4是国密算法,由国家密码局发布,分组长度为128比特,密钥长度为128比特。
解密方法
拿到密钥与密文,确认加密模式就可以直接在cipherchef里面解密.
识别方法
SM4也有着 S盒、FK、CK几个常量表,所以使用插件也可以自动化识别。
非对称加密
RSA
加密&解密
- 取两个大素数p,q(p!=q),计算N = p*q
- 求φ(N) = phi = r = (p-1)*(q-1)
- 选择一个小于r的整数e(r与e互质),用此e求d,使得e*d = 1(mod r)
- 加密: 用公式c = $n^e$ mod N
- 解密:
- d=$e^−1$(modφ(N))
- n = $c^d$ mod N
识别方法
- 对于RSA的识别,关键是对于大数运算库函数的识别,常见的大数运算库有:GMP、Miracl
或者一些密码学的库 OpenSSL、Crypto++、libtomcrypt(用的GMP) 也有着对应的实现.- 静态:可能会去符号表,存在于string中
- 动态:动态链接不能去符号表,会直接看到库
- 一些特殊数字,e = 65537 = 0x10001
解密
import gmpy2 # 计算大整数模块
import libnum
import rsa
from Crypto.PublicKey import RSA # 安装时安装pycryptodome模块
# 已知:p,q,e,c
def known_p_q_e_c():
p = int(input('请输入一个素数p:'))
q = int(input('请输入另一个素数q:'))
e = int(input('请输入公钥e:'))
c = int(input('请输入密文c:'))
d = gmpy2.invert(e, (p - 1) * (q - 1))
m = gmpy2.powmod(c, d, p * q)
return d, m
# 已知:n(较小,不超过256bit),e,c
def known_nmin_e_c():
n = int(input('请输入一个整数n:'))
e = int(input('请输入公钥e:'))
c = int(input('请输入密文c:'))
divisor = libnum.factorize(n) # 因式分解
p = int(list(divisor.keys())[0])
q = int(list(divisor.keys())[1])
d = gmpy2.invert(e, (p - 1) * (q - 1))
m = gmpy2.powmod(c, d, n)
print(f'素数p:{p}\n素数q:{q}')
return d, m
# 已知:n,e1,c1,e2,c2
def known_n_e1_c1_e2_c2():
n = int(input('请输入一个整数n:'))
e1 = int(input('请输入公钥e1:'))
c1 = int(input('请输入密文c1:'))
e2 = int(input('请输入公钥e2:'))
c2 = int(input('请输入密文c2:'))
s, s1, s2 = gmpy2.gcdext(e1, e2) # 扩展欧几里得算法
if s1 < 0:
s1 = - s1
c1 = gmpy2.invert(c1, n)
elif s2 < 0:
s2 = - s2
c2 = gmpy2.invert(c2, n)
m = (pow(c1, s1, n) * pow(c2, s2, n)) % n
return m
# 已知:n,e(非常小),c
def known_n_emin_c():
n = int(input('请输入一个整数n:'))
e = int(input('请输入公钥e:'))
c = int(input('请输入密文c:'))
k = 0
while True:
m, flag = gmpy2.iroot(c + k * n, e)
if flag == True:
return m
k += 1
# 已知:公钥文件publickey_file
def known_publickey_file():
publickey_file = input('请输入公钥文件路径:')
public = RSA.importKey(open(publickey_file).read()) # 公钥解析
print(f'整数n:{public.n}\n公钥e:{public.e}')
# 已知:加密文件cfile,p,q,e
def known_cflie_p_q_e():
cfile = input('请输入加密文件路径:')
p = int(input('请输入一个素数p:'))
q = int(input('请输入另一个素数q:'))
e = int(input('请输入公钥e:'))
d = gmpy2.invert(e, (p - 1) * (q - 1))
key = rsa.PrivateKey(p * q, e, d, p, q) # 制定新的密钥对
m = libnum.s2n(rsa.decrypt(open(cfile, 'rb').read(), key)) # 使用密钥对文件进行解密,再转换成数字
return d, m
# 已知:p1~pn,e,c
def known_p1_pn_e_c():
x = int(input('请输入n分解的质因数个数:'))
list_p = []
pq = 1
n = 1
for index in range(x):
tmp = int(input(f'请输入质因子p{index + 1}:'))
list_p.append(tmp)
pq *= tmp - 1
n *= tmp
e = int(input('请输入公钥e:'))
c = int(input('请输入密文c:'))
d = gmpy2.invert(e, pq)
m = gmpy2.powmod(c, d, n)
return d, m
# 已知:p,q,dp,dq,c
def known_p_q_dp_dq_c():
p = int(input('请输入一个素数p:'))
q = int(input('请输入另一个素数q:'))
dp = int(input('请输入d模(p-1):'))
dq = int(input('请输入d模(q-1):'))
c = int(input('请输入密文c:'))
mp = gmpy2.powmod(c, dp, p)
mq = gmpy2.powmod(c, dq, q)
m = (((mp - mq) * gmpy2.invert(q, p)) % p) * q + mq
return m
# 已知:n,e,dp,c
def known_n_e_dp_c():
n = int(input('请输入一个整数n:'))
e = int(input('请输入公钥e:'))
dp = int(input('请输入d模(p-1):'))
c = int(input('请输入密文c:'))
for x in range(1, e):
if (dp * e - 1) % x == 0:
if n % (((dp * e - 1) // x) + 1) == 0:
p = ((dp * e - 1) // x) + 1
q = n // p
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = gmpy2.powmod(c, d, n)
return d, m
# 已知:p+q,(p+1)*(q+1),d,c
def known_paq_pa1mqa1_d_c():
paq = int(input('请输入p+q:'))
pa1mqa1 = int(input('请输入(p+1)*(q+1):'))
d = int(input('请输入私钥d:'))
c = int(input('请输入密文c:'))
n = pa1mqa1 - paq - 1
m = gmpy2.powmod(c, d, n)
return d, m
# 已知:e,n组、c组
def known_e_ngroup_cgroup():
e = int(input('请输入公钥e:'))
ngroup = list(map(int, input('请输入n组(空格隔开):').split()))
cgroup = list(map(int, input('请输入c组(空格隔开):').split()))
for count1 in range(len(ngroup)):
for count2 in range(len(ngroup)):
if count1 != count2:
if gmpy2.gcd(ngroup[count1], ngroup[count2]) != 1 and gmpy2.is_prime(gmpy2.gcd(ngroup[count1], ngroup[count2])): # 求公因数并为质数
p = gmpy2.gcd(ngroup[count1], ngroup[count2])
if gmpy2.is_prime(ngroup[count1] // p): # 只有当p、q都为质数时计算才有意义
q = ngroup[count1] // p
d = gmpy2.invert(e, (p - 1) * (q - 1))
m = pow(cgroup[count1], d, ngroup[count1])
return d, m
# 已知:n组(两两互质)、c组
def known_ngroup_cgroup():
ngroup = list(map(int, input('请输入n组(空格隔开):').split()))
cgroup = list(map(int, input('请输入c组(空格隔开):').split()))
e_begin = int(input('请输入e的最小范围(不小于2):'))
e_finish = int(input('请输入e的最大范围:'))
N = 1
for n in ngroup:
N *= n
for e in range(e_begin, e_finish):
m_power_e = 0
for count in range(len(ngroup)):
m_power_e += cgroup[count] * N // ngroup[count] * gmpy2.invert(N // ngroup[count], ngroup[count])
m, flag = gmpy2.iroot(m_power_e % N, e)
if flag:
return m
# 已知:p、q、e(与phi不互素)、c
def known_p_q_eprime_c():
p = int(input('请输入一个素数p:'))
q = int(input('请输入另一个素数q:'))
e = int(input('请输入公钥e:'))
c = int(input('请输入密文c:'))
n = p * q
phi = (p - 1) * (q - 1)
t = gmpy2.gcd(e, phi)
d = gmpy2.invert(e // t, phi)
m = pow(c, d, n)
return int(gmpy2.iroot(m, t)[0]) # 求m开t次根
d = None
m = None
condition = int(input('''已知条件:1、p,q,e,c
2、n(较小),e,c
3、n,e1,c1,e2,c2
4、n,e(非常小),c
5、公钥解析(公钥文件)
6、加密文件,p,q,e,d
7、p1~pn(多个质因子),e,c
8、p,q,dp,dq,c
9、n,e,dp,c
10、p+q,(p+1)*(q+1),d,c
11、e,n组、c组
12、n组(两两互质)、c组
13、已知:p、q、e(与phi不互素)、c
请输入序号:'''))
if condition == 1:
d, m = known_p_q_e_c()
elif condition == 2:
d, m = known_nmin_e_c()
elif condition == 3:
m = known_n_e1_c1_e2_c2()
elif condition == 4:
m = known_n_emin_c()
elif condition == 5:
known_publickey_file()
elif condition == 6:
d, m = known_cflie_p_q_e()
elif condition == 7:
d, m = known_p1_pn_e_c()
elif condition == 8:
m = known_p_q_dp_dq_c()
elif condition == 9:
d, m = known_n_e_dp_c()
elif condition == 10:
d, m = known_paq_pa1mqa1_d_c()
elif condition == 11:
d, m = known_e_ngroup_cgroup()
elif condition == 12:
m = known_ngroup_cgroup()
elif condition == 13:
m = known_p_q_eprime_c()
else:
print('请输入正确的序号!')
print(f'私钥d:{d}')
print(f'明文m:{m}')
if m != None:
print(f'字符明文:{libnum.n2s(int(m)).decode("utf-8")}')
# 数字转字符串,再进行utf-8编码
单向散列函数
MD5
-
MD5消息摘要算法(MD5,Message-Digest Algorithm)
-
代码实现
// Constants are the integer part of the sines of integers (in radians) * 2^32. const uint32_t k[64] = { 0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501, 0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821, 0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa, 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8, 0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a, 0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70, 0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05, 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665, 0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1, 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1, 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391 }; // r specifies the per-round shift amounts const uint32_t r[] = {7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21}; #define LEFTROTATE(x, c) (((x) << (c)) | ((x) >> (32 - (c)))) void to_bytes(uint32_t val, uint8_t *bytes) { bytes[0] = (uint8_t) val; bytes[1] = (uint8_t) (val >> 8); bytes[2] = (uint8_t) (val >> 16); bytes[3] = (uint8_t) (val >> 24); } uint32_t to_int32(const uint8_t *bytes) { return (uint32_t) bytes[0] | ((uint32_t) bytes[1] << 8) | ((uint32_t) bytes[2] << 16) | ((uint32_t) bytes[3] << 24); } void md5(const uint8_t *initial_msg, size_t initial_len, uint8_t *digest) { // These vars will contain the hash uint32_t h0, h1, h2, h3; // Message (to prepare) uint8_t *msg = NULL; size_t new_len, offset; uint32_t w[16]; uint32_t a, b, c, d, i, f, g, temp; // Initialize variables - simple count in nibbles: h0 = 0x67452301; h1 = 0xefcdab89; h2 = 0x98badcfe; h3 = 0x10325476; //Pre-processing: //append "1" bit to message //append "0" bits until message length in bits ≡ 448 (mod 512) //append length mod (2^64) to message for (new_len = initial_len + 1; new_len % (512/8) != 448/8; new_len++); msg = (uint8_t*)malloc(new_len + 8); memcpy(msg, initial_msg, initial_len); msg[initial_len] = 0x80; // append the "1" bit; most significant bit is "first" for (offset = initial_len + 1; offset < new_len; offset++) msg[offset] = 0; // append "0" bits // append the len in bits at the end of the buffer. to_bytes(initial_len*8, msg + new_len); // initial_len>>29 == initial_len*8>>32, but avoids overflow. to_bytes(initial_len>>29, msg + new_len + 4); // Process the message in successive 512-bit chunks: //for each 512-bit chunk of message: for(offset=0; offset<new_len; offset += (512/8)) { // break chunk into sixteen 32-bit words w[j], 0 ≤ j ≤ 15 for (i = 0; i < 16; i++) w[i] = to_int32(msg + offset + i*4); // Initialize hash value for this chunk: a = h0; b = h1; c = h2; d = h3; // Main loop: for(i = 0; i<64; i++) { if (i < 16) { f = (b & c) | ((~b) & d); // F g = i; } else if (i < 32) { f = (d & b) | ((~d) & c); // G g = (5*i + 1) % 16; } else if (i < 48) { f = b ^ c ^ d; // H g = (3*i + 5) % 16; } else { f = c ^ (b | (~d)); // I g = (7*i) % 16; } temp = d; d = c; c = b; b = b + LEFTROTATE((a + f + k[i] + w[g]), r[i]); a = temp; } // Add this chunk's hash to result so far: h0 += a; h1 += b; h2 += c; h3 += d; } // cleanup free(msg); //var char digest[16] := h0 append h1 append h2 append h3 //(Output is in little-endian) to_bytes(h0, digest); to_bytes(h1, digest + 4); to_bytes(h2, digest + 8); to_bytes(h3, digest + 12); } -
识别
- 首先常数 0x67452301, 0xefcdab89, 0x98badcfe, 0x10325476,是识别MD5的一大关键,其次就是 k 和 r 两个表(这俩不一定会写成数组的格式,也有可能硬编码到代码里),一般来说MD5是可以通过插件识别的。
BaseXX系列
base64
魔改:
- 换表
- 将一轮输出的四个字符改变顺序,或将四个字符对应的bit换位一下
- 输出结果进行异或
BaseKnowledge
IV
- 作用
- 防止相同的明文产生相同的密文
- 增强安全性: IV能有效防止重放攻击(patch密文)和某些模式下的分析攻击,特别是在某些分组加密模式(如CBC模式)中,IV的引入可以避免加密块之间存在的相似性,从而进一步提升加密强度。
- 本质:
- IV是加密算法中用来引入随机性或不可预测性的一个输入值,其本身并不需要保密,但它必须是唯一且随机生成的,至少对每次加密来说不能重复使用。IV本质上与密钥不同,密钥是保持加密解密过程的机密性,而IV只是引入随机性的手段。(但是对于真正做逆向的时候会是什么情况,下次遇到仔细分析)
Salt
定义: Salt 是在对密码或敏感数据做哈希(如 SHA256)或加密前,随机生成并与原始数据拼接,再进行处理的随机字符串。
使用实例:
- 用户密码: password123
- salt: 12345
拼接后为password12312345再做hash,并以salt+哈希值的形式存储.
分组大小
- 分组大小指的是加密算法处理的固定数据块的大小(例如AES分组大小为128bit)
- 在每次加密/解密时,AES会将输入的数据分成若干个128bit的数据块
- 如果输入的数据长度超过128位,AES会将数据分块处理.如果数据不足128位,通常会进行填充(padding)以凑满128位。
- 例如
- 如果明文数据为64字节(512bit),AES将这64字节的数据分为四个128位的分组,逐一进行加解密
- 如果明文数据不是128位的整数倍(比如输入是150位的明文),就会使用填充算法来凑齐到128位的倍数。
AEAD(Authenticated Encryption with Associated Data)
定义: AEAD 是一种同时实现机密性(Encryption)与完整性认证(Authentication)的对称加密模式,允许在加密数据的同时对附加的非加密数据(AAD)提供完整性验证。
作用: 解决传统对称加密解密后未知密钥正确与否的问题,例如:使用一个密钥可能解出意思明文的内容,但实际上该密钥与结果是错误的.
工作原理:
- 加密时,同时生成一个 认证标签(Tag)
- 解密时,除了还原密文,还会验证 Tag 是否匹配
> 验证方式: 用key,IV,AAD等重新生成一个Tag,与传入的Tag进行匹配
- 如果密钥或数据被篡改,Tag 校验失败,解密直接失败,不给你任何输出
AAD(Additional Authenticated Data,附加认证数据):
- 以明文形式传输
- 参与生成Tag
- 如果 AAD 传输中被篡改,解密时 Tag 校验会失败,数据解密失败
Mode of operation
注: 部分搬运
密码学中,分组密码的工作模式(mode of operation)允许使用同一个分组密码密钥对多于一块的数据进行加密,并保证其安全性。
分组密码自身只能加密长度等于密码分组长度的单块数据,若要加密变长数据,则数据必须先被划分为一些单独的密码块。通常而言,最后一块数据也需要使用合适填充方式将数据扩展到符合密码块大小的长度。一种工作模式描述了加密每一数据块的过程,并常常使用基于一个通常称为初始化向量的附加输入值以进行随机化,以保证安全。
电子密码本(ECB)
最简单的加密模式即为电子密码本(Electronic codebook,ECB)模式。需要加密的消息按照块密码的块大小被分为数个块,并对每个块进行独立加密。
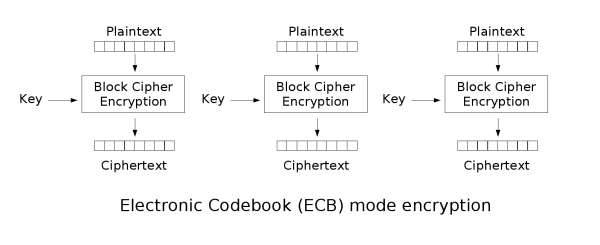
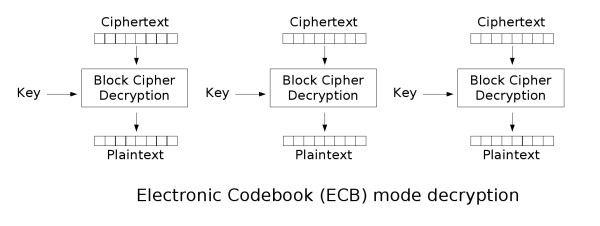
密码块链接(CBC)
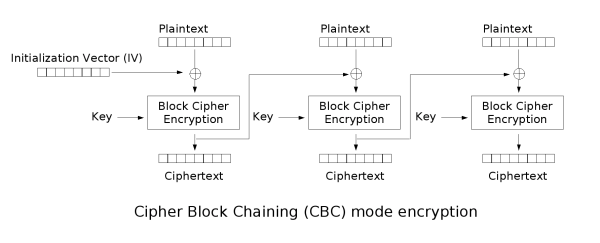
在CBC模式中,每个明文块先与前一个密文块进行异或后,再进行加密。在这种方法中,每个密文块都依赖于它前面的所有明文块。同时,为了保证每条消息的唯一性,在第一个块中需要使用初始化向量。
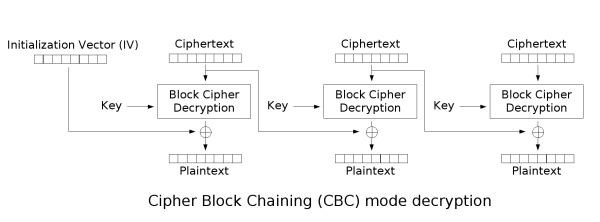
密文反馈(CFB)
密文反馈(CFB,Cipher feedback)模式类似于CBC,可以将块密码变为自同步的流密码;工作过程亦非常相似,CFB的解密过程几乎就是颠倒的CBC的加密过程:
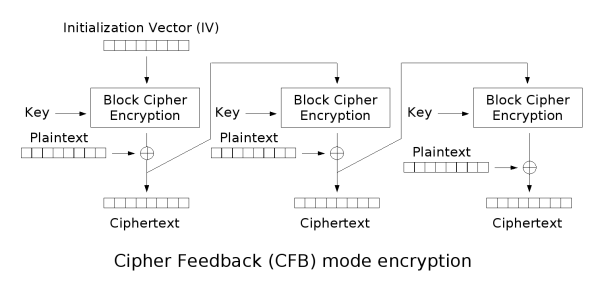
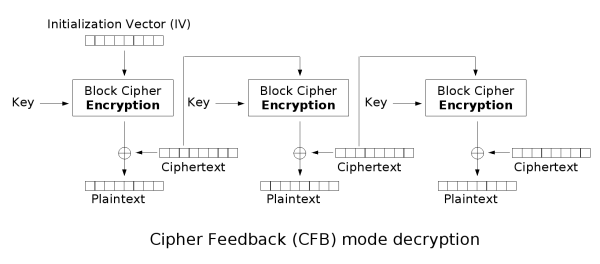
输出反馈(OFB)
输出反馈模式(Output feedback, OFB)可以将块密码变成同步的流密码。它产生密钥流的块,然后将其与明文块进行异或,得到密文。与其它流密码一样,密文中一个位的翻转会使明文中同样位置的位也产生翻转。这种特性使得许多错误校正码,例如奇偶校验位,即使在加密前计算,而在加密后进行校验也可以得出正确结果。
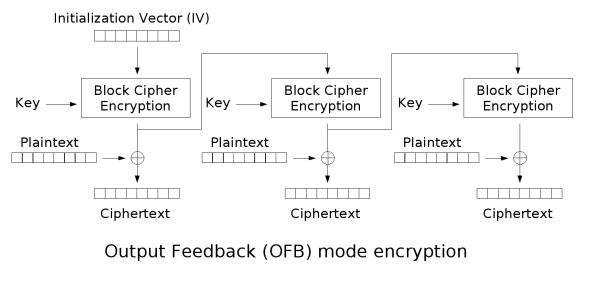
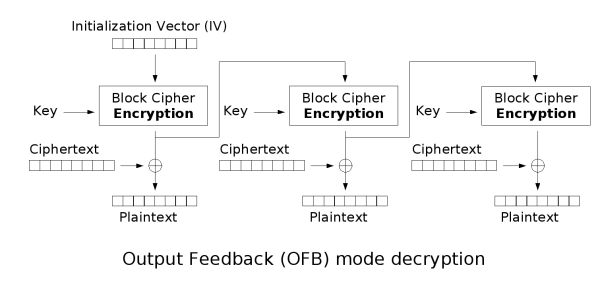
伽罗瓦计数器模式(GCM)
AES-GCM 加密 :
| 输入(Input) | 说明 |
|---|---|
| Key | 对称加密密钥(128/192/256 位) |
| IV(Nonce) | 初始化向量,一般12字节(96位) |
| Plaintext(明文) | 需要加密的数据 |
| AAD(附加认证数据,可选) | 不加密但参与认证的数据 |
| 输出(Output) | 说明 |
|---|---|
| Ciphertext(密文) | 加密后的数据 |
| Tag(认证标签) | 用于完整性和认证的校验标签(通常16字节) |
| AES-GCM 解密 : |
| 输入(Input) | 说明 |
|---|---|
| Key | 与加密时相同的对称密钥 |
| IV(Nonce) | 与加密时相同的初始化向量 |
| Ciphertext(密文) | 加密后的数据 |
| AAD(附加认证数据) | 与加密时相同的附加认证数据 |
| Tag(认证标签) | 加密时生成并附带的认证标签 |
| 输出(Output) | 说明 |
|---|---|
| Plaintext(明文) | 解密得到的原始数据(如果认证成功) |
| 错误/失败 | 如果认证标签不匹配,解密失败 |
注意
- 在遇到移位操作时,ida识为什么类型int or uint,再解密时便使用什么类型,如果int型密文报错便(int)强转一下



 浙公网安备 33010602011771号
浙公网安备 33010602011771号