P6646 [CCO 2020] Shopping Plans

严肃学习。写的很冗余，其实理解起来并不困难，只是想尽量将优化状态的过程描述出来。

求前 \(k\) 优，考虑设计状态 \(S\) 满足：

· 每个子段被唯一的状态 \(S\) 表示。

· \(w(S'\in nxt(S))\le w(S)\)

· \(pre(S)\) 唯一。

而每轮取出最优的 \(S\)，拓展出 \(nxt(S)\) 参与下一轮比较。

用堆维护最优状态即可。容易证明该策略是优秀的。

这题很复杂啊。先考虑限制特殊的情况。

\(m=1\)

此时相当于求从 \(n\) 个数，\(\sum_{i\in P}a_i\) 前 \(k\) 小的 \(P,|P|\in[l,r]\)，考虑如何设计状态。将 \(a\) 升序排序后初始状态必定形如选一段前缀，先将 \([1,i],i\in[l,r]\) 加入。

设计状态 \((|P|,sum)\)。考虑拓展，每种情况唯一表示则 \(|S|\) 不变，\(w(nxt(S))\ge w(S)\) 则每次相当于将其中一个物品替换为更大。加一维 \((|P|,sum,P)\)，每次替换一个，发现一个 \(P\) 能由多个状态替换过来（例如 \(100111\) 由 \(110110\)，\(101110\) 转移），考虑钦定每次替换的物品所在位置 \(id\)，\((sum,P,id)\)。

还有问题是 \(110011,101011\) 都能转移到 \(110111\)，将状态间转移看作图：

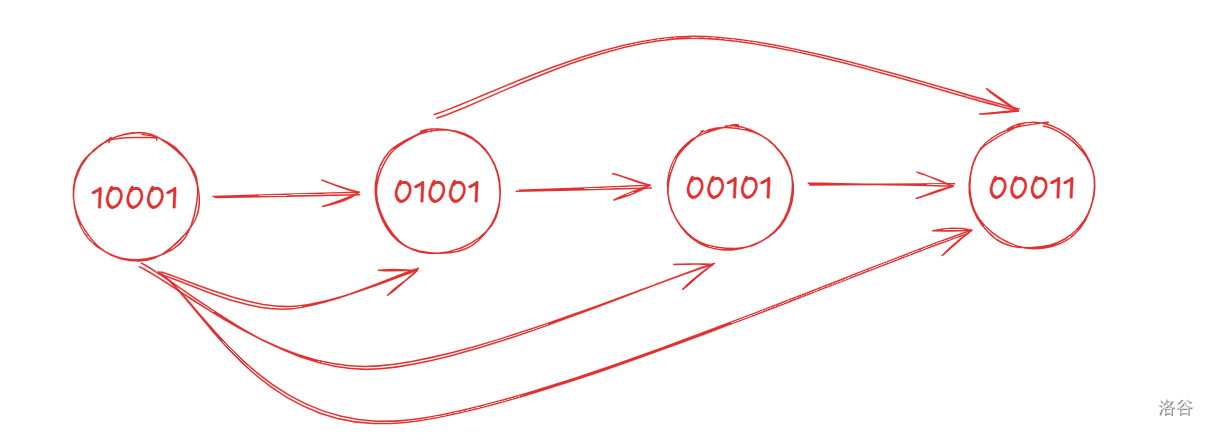
还是重复很多，到这里其实容易想到将物品固定替换为其下一个。

若要用来替换当前物品的元素 \(t\) 已经在 \(P\) 中，则不能再对该物品进行替换操作。

否则等价转移至 \(id\) 为 \(t\)，\(P'\) 为 \((P\setminus t)\bigcup \{t+1\}\) 的状态，不符合转移方向。

\[(sum,P,id)\to (sum-v_{id}+v_{id+1},(P\setminus{id})\bigcup\{id+1\},id+1),id+1\notin P \]

\[(sum,P,id)\to (sum,P,x),x< id\wedge x\in P \]

但是第二个转移实际上 \(P\) 没有任何变化，则 \(P\) 没有被唯一的状态表示。考虑强制 \(x\) 替换一次。

\[(sum,P,id)\to (sum-v_x+x_{x+1},(P\setminus x)\bigcup \{x+1\},x+1),x<id\wedge x\in P \]

记录 \(P\) 是不现实的，考虑实际上用了 \(P\) 记录的哪些信息：

1. 下一个在 \(P\) 中且 \(>id\) 的位置。

2. 符合条件的 \(x\)。

第一个显然能多一维状态数 \(O(n)\) \(nxt\) 表示，而第二个根据初始状态实际上能发现没有进行操作的数是一个前缀，且对于 \(i\) 必定在 \(i+1\) 操作之后才能进行操作，所以记录 \(lst\) 为前缀最后一个没有进行操作的位置。

\[(sum,nxt,lst,id)\to (sum-v_{id}+v_{id+1},nxt,lst,id+1),id+1<nxt \]

\[(sum,nxt,lst,id)\to (sum-v_{lst}+v_{lst+1},id,lst-1,lst+1) \]

和上面的转移是等价的。

于是就有 \(O(k\log n)\) 的做法。

\(m>1\)

将每个种类中按 \(m=1\) 的做法得到第 \(k\) 小的选法看作第 \(k\) 个物品，则相当于从每个种类中选择一个物品。这个可以封装等需要的时候再求。

考虑状态 \((W,sum)\)，其中 \(W\) 是每个种类的选择情况的集合，\(sum\) 是权值和。有重复，与 \(m=1\) 中类似，考虑钦定当前操作的 \(id\)，且转移方向从小到大，记录选择的是第 \(k\) 小的方案。

\[(id,k,sum)\to (id,k+1,sum-ans_{id,k}+ans_{id,k+1}) \]

\[(id,k,sum)\to (id+1,2.sum-ans_{id+1,1}+ans_{id+1,2}) \]

第二个转移同样钦定转移，但是这样会有问题，上文中能钦定转移是因为所有 \(i\) 必须在 \(i+1\) 操作后才能操作，所以若操作下一次的对象必定位 \(lst\)，但现在没有这个性质，不同种类的转移并不相依赖。若要钦定转移则需要直接转移到下一步操作的种类。

\[(id,k,sum)\to (id',2,sum-ans_{id',1}+ans_{id',2}),id'>id \]

但这样 \(|nxt(S)|\) 是 \(O(M)\) 级别的，拓展一次也需要 \(O(M)\)。

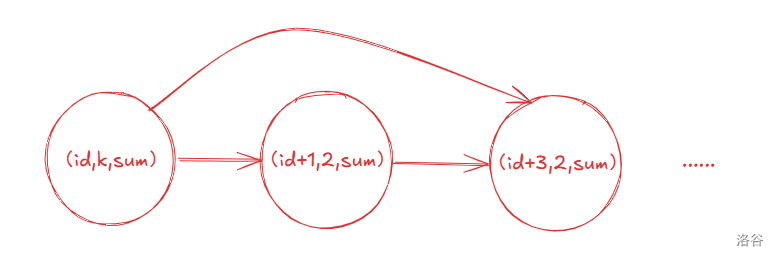
考虑去掉所有 \((id,,)\to (id+x,2,),x>1\) 的转移，则需要一种转移能描述集合不转移且所有情况能唯一表示。

在 \((id+1,2,),(id+2,2,)\) 之间加入一种转移描述原本转移到两种状态的 \(\Delta\)，也就是：

\[(id,2,sum)\to (id+1,2,sum-ans_{id,2}+ans_{id,1}-ans_{id+1,1}+ans_{id+1,2}) \]

而 \(ans_{id,2}+ans_{id,1}-ans_{id+1,1}+ans_{id+1,2}\) 可能 \(<0\) 就不满足 \(w(nxt(S))\ge w(S)\)，其实只需要按 \(ans_{i,2}-ans_{i,1}\) 排序后就好了。

则将 \(|nxt(S)|\) 量级降到 \(O(1)\) 每次拓展也是 \(O(1)\)。于是也是复杂度 \(O(k\log n)\)。注意一下若初始状态是 \((1,1,minsum)\) 则不能转移到 \((2,2,)\) 否则会与第三种转移重复。看情况实现吧。

Takanshi Rikka

#include<bits/stdc++.h>
using namespace std;
#define fin(x) freopen(#x".in","r",stdin)
#define fout(x) freopen(#x".out","w",stdout)
#define fr(x) fin(x),fout(x);
#define Fr(x,y) fin(x),fout(y)
#define INPUT(_1,_2,FILE,...) FILE
#define IO(...) INPUT(__VA_ARGS__,Fr,fr)(__VA_ARGS__)
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define il inline
#define cfast ios::sync_with_stdio(false);cin.tie(0),cout.tie(0)
#define ll long long
#define ull unsigned long long
#define intz(x,y) memset((x),(y),sizeof((x)))
inline void cmx(auto &x,ll y){if(y>x)x=y;}
inline void cmn(auto &x,ll y){if(y<x)x=y;}
inline int max(vector<int>w){int res=-1e9;for(int i:w)cmx(res,i);return res;}
#define pcount(x) __builtin_popcount(x)
#define int ll
const int N=2e5+5,inf=1e15;
int n,m,k,id[N];
struct state{
	basic_string<int>w,ans;
	int l,r;
	struct node{
		int x,y,z,sum;
		il friend bool operator<(node x,node y){
			return x.sum>y.sum;
		}
	};priority_queue<node>dl;
	il void pb(int x){w.pb(x);}
	il void calc(int x){
		if(x<ans.size())return;
		if(!dl.size())return ans.pb(inf),void();
		node u=dl.top();dl.pop();ans.pb(u.sum);
		if(u.y>0&&u.y+1<u.z)dl.push({u.x,u.y+1,u.z,u.sum-w[u.y]+w[u.y+1]});
		if(u.x>0&&u.x+1<u.y)dl.push({u.x-1,u.x+1,u.y,u.sum-w[u.x]+w[u.x+1]});
	}
	il void init(){
		sort(w.begin(),w.end());
		if(l>=w.size()||l>r){for(int i=1;i<=k;i++)cout<<-1<<'\n';exit(0);}
		cmn(r,w.size()-1);int s=0;
		for(int i=0;i<=r;i++)s+=w[i],
			(i>=l?(dl.push({i-1,i,(int)w.size(),s}),1):0);
		ans.pb(0),calc(1),calc(2);
	}
}t[N];
struct State{
	basic_string<int>ans;
	struct node{
		int x,y,sum;
		il friend bool operator<(node x,node y){
			return x.sum>y.sum;
		}
	};priority_queue<node>dl;
	il void calc(int x){
		if(x<ans.size())return;
		if(!dl.size())return ans.pb(inf),void();
		node u=dl.top();dl.pop();ans.pb(u.sum);
		if(u.y>1&&u.x+1<=m)dl.push({u.x+1,2,u.sum+t[id[u.x+1]].ans[2]-t[id[u.x+1]].ans[1]});
		t[id[u.x]].calc(u.y+1),
		dl.push({u.x,u.y+1,u.sum+t[id[u.x]].ans[u.y+1]-t[id[u.x]].ans[u.y]});
		if(u.x+1<=m&&u.y==2)
			dl.push({u.x+1,2,u.sum-t[id[u.x]].ans[2]+t[id[u.x]].ans[1]+t[id[u.x+1]].ans[2]-t[id[u.x+1]].ans[1]});
	}
	il void init(int S){dl.push({1,1,S}),ans.pb(0);}
}q;
void UesugiErii(){
	cin>>n>>m>>k;
	for(int i=1;i<=m;i++)t[i].pb(0);
	for(int i=1,c,x;i<=n;i++)
		cin>>c>>x,t[c].pb(x);
	int sum=0;
	for(int i=1;i<=m;id[i]=i,i++)
		cin>>t[i].l>>t[i].r,t[i].init(),sum+=t[i].ans[1];
	sort(id+1,id+1+m,[&](int x,int y){return t[x].ans[2]-t[x].ans[1]<t[y].ans[2]-t[y].ans[1];});
	q.init(sum);
	for(int i=1;i<=k;i++){
		q.calc(i);
		if(q.ans[i]>=inf){for(int j=i;j<=k;j++)cout<<-1<<'\n';return;}
		cout<<q.ans[i]<<'\n';
	}
}
signed main(){
	//IO();
	cfast;
	int _=1;//cin>>_;
	for(;_;_--)UesugiErii();
	return 0;
}