CF1090J Two Prefixes

完成了一系列字符串大学习。

考虑刻画相同的两种情况。

\(s:[1,x]+t:[1,y]=s:[1,x']+t:[1,y']\)。假定 \(y'<y\)。

也就是说 \(t:[1,y']=t:[y-y'+1,y]\)。即 \(t:[1,y']\) 为 \(t:[1,y]\) 的 border。

考虑取 \(t:[1,y],t:[1,y']\) 时有多少种 \(x\) 能满足相等，发现等同于 \(t:[1,y-y']\) 在 \(s\) 中出现次数。

也就是需要求出 \(t\) 每个前缀在 \(s\) 中作为真子串的出现次数 \(c\)。

还是第一次看到这个怎么求。建出 \(t\) 的 fail 树，\(s\) 在 \(t\) 中匹配到 \(t:[1,i]\) 对应点 \(u\)，则相当于以 fail 树上跟到 \(u\) 的路径 \(+1\)。这里有一个细节，要求真子串，所以当 \(s\) 被完全匹配时 \(u\) 这个点不能加。

知道怎么求出 \(c\)，再考虑计数。

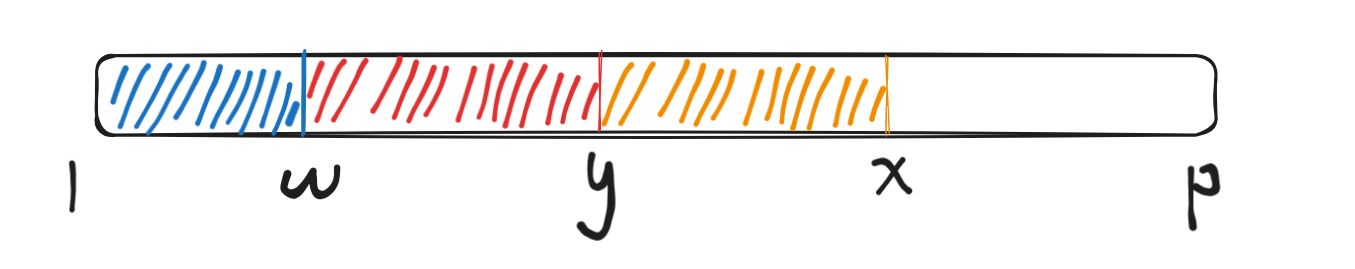
如果 \(t:[1,i]\) 对其所有 border \(t:[1,j]\) 都贡献 \(c_{i-j}\)，发现会算重。

考虑 \(t:[1,i]\) 两个 border \(t:[1,j],t:[1,k],k<j\) 分别贡献了 \(c_{i-j},c_{i-k}\)。

上图 \(s:[w,p]=t:[1,i]\)，\(s:[w,x]=t:[1,i-k]\)，\(s:[w,y]=t:[1,i-j]\)（根据 border 的性质一定存在 \(s:[w,y]=t:[1,i-j],w<y<x\)）。

则有：

\(s:[1,w]+t:[1,i] \\=s:[1,x]+t:[1,i-k] \\=s:[1,y]+t:[1,i-j]\)

需要去除的是 \(s:[1,w]+t:[1,i]\) 的贡献，所以这里就已经算重了。

对于长度越长的 border \(t:[1,j]\)，\(t:[1,i-j]\) 越短，在 \(s\) 中的出现条件越宽松且对于所有 \(k<j,t:[1,i-k]\) 在 \(s\) 作为子串 \([l,r]\) 出现均会存在前缀 \([l,r'],r'<r\) 为 \(t:[1,i-j]\)。

所以对于每个 \(t:[1,i]\) 仅需对于其最长 border 统计答案即可。

#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define fin(x) freopen(#x".in","r",stdin)
#define fout(x) freopen(#x".out","w",stdout)
#define fr(x) fin(x),fout(x);
#define Fr(x,y) fin(x),fout(y)
#define INPUT(_1,_2,FILE,...) FILE
#define IO(...) INPUT(__VA_ARGS__,Fr,fr)(__VA_ARGS__)
using namespace std;
using namespace __gnu_pbds;
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define cfast ios::sync_with_stdio(false);cin.tie(0),cout.tie(0)
#define ll long long
#define ull unsigned long long
#define intz(x,y) memset((x),(y),sizeof((x)))
char *p1,*p2,buf[100000];
#define nc() (p1==p2 && (p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
#define tup(x) array<int,(x)>
inline ll read(){
    ll x=0,f=1;char ch=nc();
    while(ch<48||ch>57){if(ch=='-')f=-1;ch=nc();}
    while(ch>=48&&ch<=57)x=x*10+ch-48,ch=nc();
   	return x*f;
}
//void write(int x){cout<<x<<' ';}
//void write(pii x){cout<<"P("<<x.fi<<','<<x.se<<")\n";}
//void write(vector<auto>x){for(auto i:x)write(i);cout<<'\n';}
//void write(auto *a,int l,int r){for(int i=l;i<=r;i++)write(a[i]);cout<<'\n';}
inline ll lowbit(ll x){return x&-x;}
inline int pcount(ll x){
	for(int i=0,res=0;;res+=(x>>i)&1,i++)
		if(i>60)return res;
}

//struct mt{
//	ll v;
//	mt(){v=0;}
//	mt(int x){this->v=x;}
//	inline mt operator+(mt x){return {(v+x.v)%mod};}
//	inline mt operator-(mt x){return {(v+mod-x.v)%mod};}
//	inline mt operator*(mt x){return {1ll*v*x.v%mod};}
//};
//inline void add(mt &x,mt y){x=x+y;}
//mt qp(mt x,int y){mt res(1);for(;y;x=x*x,y>>=1)if(y&1)res=res*x;return res;}
const int N=1e5+5;
string s,t;int nxt[N],c[N]; 
inline void UesugiErii(){
	cin>>s>>t,s=' '+s,t=' '+t;
	int n=s.size()-1,m=t.size()-1;ll ans=0;
	for(int i=2,j=0;i<=m;i++){
		while(j&&t[i]!=t[j+1])j=nxt[j];
		if(t[i]==t[j+1])++j;nxt[i]=j;
	}
	for(int i=1,j=0;i<=n;i++){
		while(j&&s[i]!=t[j+1])j=nxt[j];
		if(s[i]==t[j+1])++j;
		++(i==j?c[nxt[i]]:c[j]);
	}
	for(int i=m;i;i--)c[nxt[i]]+=c[i];
	for(int i=1;i<=m;i++)
		if(nxt[i])ans+=c[i-nxt[i]];
	cout<<1ll*n*m-ans;
}
signed main(){
	//IO();
	cfast;
	int _=1;//cin>>_;
	for(;_;_--)UesugiErii();
	return 0;
}