CF506E Mr. Kitayuta's Gift

没见过的套路，还是很神的。模数写成 \(10^4+5\) 调了 1h /fn。

参考题解 修仙-Otomachi_Una_

首先记 \(m=|S|+n\)。

计数考虑 dp。插入字符使其成为回文串 dp 显然是困困难难的。

考虑从最终插入字符后的结果入手，则对于回文串 \(T\) 能通过 \(S\) 插入字符得到当且仅当 \(|T|=|S|+n\) 且 \(S\) 为 \(T\) 的子序列。

因为 \(T\) 是回文串，所以若是类似状态 \(f_{i,j}\) 表示前 \(i\) 个字符最多匹配到 \(S\) 第 \(j\) 个字符则会有后效性。

于是设计状态 \(f_{i,l,r}\) 表示考虑 \(T\) 的前后 \(i\) 个字符，尽量匹配后 \(S\) 剩下 \(S:[l,r]\) 未匹配的方案数，则转移为：

奇数情况最后一位比较特殊，所以先钦定 \(m\) 为偶数。

1. \(S_l=S_r\)：

\(f_{i+1,l+1,r-1}\to f_{i,l,r}\)。

\(f_{i+1,l,r}\to 25\cdot f_{i,l,r}\)。

第一条转移表示 \(T_{i+1}=T_{m-i}=S_l(S_r)\) 则 \(T_{i+1}\)，\(T_{m-i}\) 只有一种选择，且 \(S_l,S_r\) 均会被匹配。

第二条转移表示 \(T_{i+1}=T_{m-i}\ne S_l(S_r)\) 则 \(T_{i+1}\)，\(T_{m-i}\) 有 25 种选择，且 \(S_l,S_r\) 均不会被匹配。

2. \(S_l\ne S_r\)：

\(f_{i+1,l+1,r}\to f_{i,l,r}\)。

\(f_{i+1,l,r-1}\to f_{i,l,r}\)。

\(f_{i+1,l,r}\to 24\cdot f_{i,l,r}\)。

前两条转移式分别表示 \(T_{i+1}=T_{m-i}=S_l\)，\(T_{i+1}=T_{m-i}=S_r\)。

第三条转移表示 \(T_{i+1}=T_{m-i}\ne S_l/S_r\) 则 \(T_{i+1}\)，\(T_{m-i}\) 只有 24 种选择，且匹配情况不变。

若 \(l>r\) 则记入状态 \(g_i\) 表示考虑前后 \(i\) 个字符匹配成功的方案数，则 \(g_{i+1}\to 26\cdot g_i\) 即任意插入一个字符。答案即为 \(g_{\frac{m}{2}}\)

暴力转移为 \(O(m|S|^2)\)。

容易发现 \(n\) 的范围而考虑矩阵优化。但若是将当前轮每个 \((l,r)\) 标号。构建矩阵，矩阵大小为 \(|S|^2\)，则时间复杂度为 \(O(|S|^6\log m)\)。依旧爆炸。

发现若是将当前轮每一个 \((l,r)\) 视作一个点，若 \((l,r)\) 能转移 \((l',r')\) 则有边 \((l,r)\to (l',r')\)。发现这样形成的图除去自环为 DAG。（貌似说是有限状态自动机，不会 /ll）。

建出的图类似（* 代表该位置已匹配）：

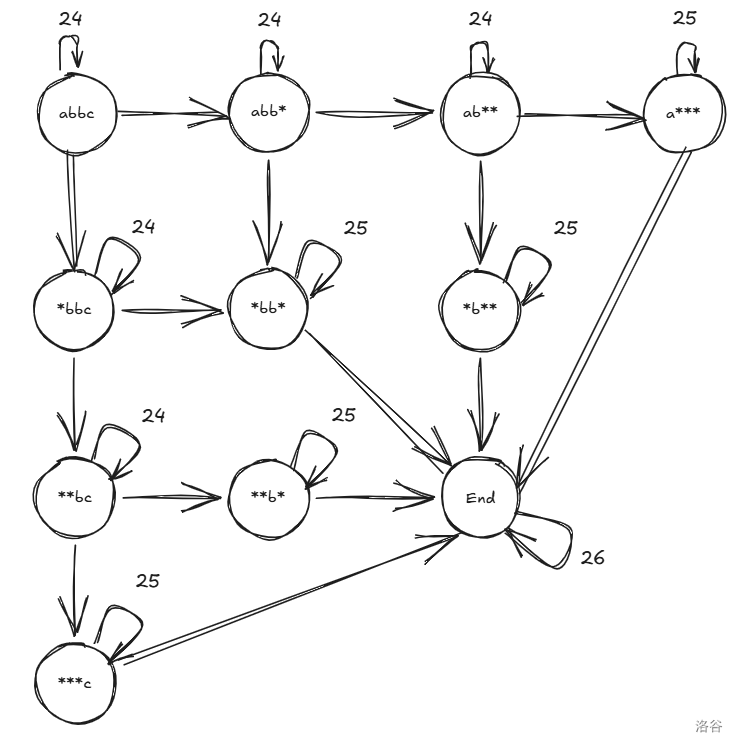
而 dp 相当于在 DAG 走 \(\frac{m}{2}\) 步且最终停在终点，权值为路径上边权的乘积。答案即为所有方案的权值和。

发现一条路径的权值实际上之与其 \(deg-24,deg-25\) 两种点的个数有关，将 \(deg=24\) 称为蓝点，\(deg=25\) 称为红点。

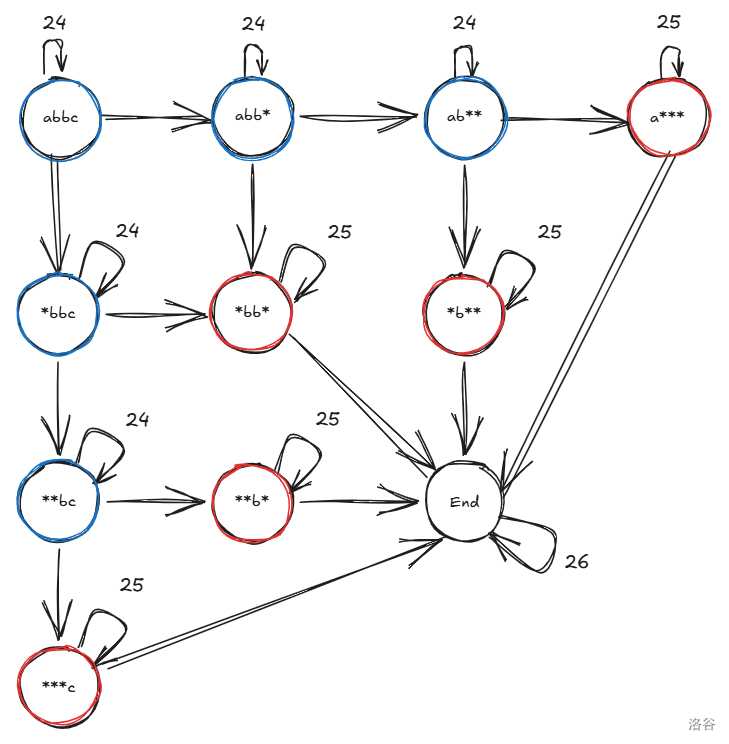
假设 \(deg-24\) 的点的个数为 \(x\)，则 \(deg-25\) 的点数为 \(y=\lceil\frac{n-x}{2}\rceil\)。

考虑两种点在 dp 中的实际意义，\(deg-24\) 相当于 \(S\) 匹配一个字符，\(deg-25\) 相当于匹配两个。最终结束状态匹配 \(n/n+1\) 个字符（n+1 个字符是因为存在 \(l=r,S_l=S_r\) 此时仍认为匹配了两个），容易得出。

于是分别从每种路径所有可能权值和、经过该种路径的方案数（不考虑自环）入手。

设经过 \(x\) 个蓝点的路径方案数 \(f_{x}\)。

对于 \(f\) 可以直接记忆化搜索 \((l,r,x)\) 表示当前还要经过 \(x\) 个蓝点，\(S:[l,r]\) 尚未匹配，得到结果，因为每一层搜索 \(O(1)\) 且不考虑自环，则每递归一层未匹配区间长度至少 -1。则最劣复杂度为 \(O(|S|)\)。

接下来考虑每种路径所有可能权值和。

若将自环上的权值视作向自己连有多少条边，则每种路径所有可能权值和即为从起点走到终点长度为 \(\frac{m}{2}\) 的路径数量，套路的矩阵快速幂算。

假设 \(x=3,y=3\)：

即为这个图从第一个蓝点 \(\frac{m}{2}\) 停在结束状态的方案数。

于是可以枚举经过蓝点个数，\(O(|S|)\) 算方案数，\(O(|S|^3\log m)\) 求出路径所有可能权值和，则这种路径对答案的贡献为两者之积。

总复杂度 \(O(|S|^4\log m)\)。还需进一步优化。

每次对对应的链做一次矩乘时间复杂度无法接受。但发现若是每个红点都连向一个结束状态。就能够一次矩乘算出经过 \(x\) 个蓝点，\(y'(y'\le y)\) 个红点的路径可能权值和。这启发按照上图的形式直接连出 \(|S|\) 个蓝点，\(|S|\) 个红点的情况，再给每个红点一个对应的结束状态。

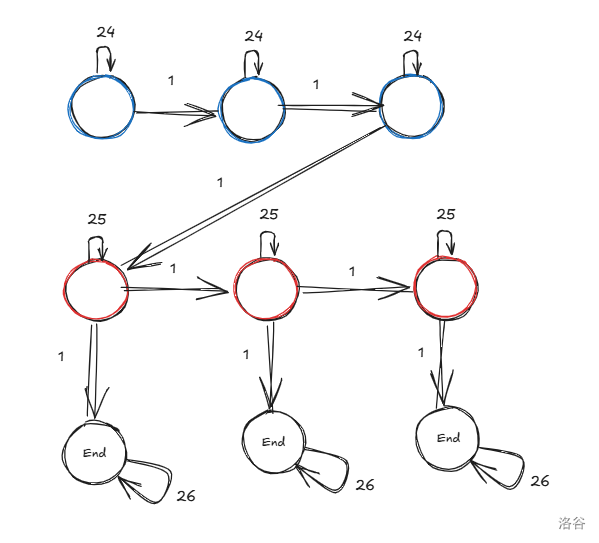
就像这样，于是就可以 \(O(|S|^3\log m)\) 预处理，\(O(1)\) 查询了。

于是复杂度优化到单词查询最劣 \(O(|S|)\)，总复杂度最劣 \(O(|S|^2+|S|^3\log m)\)。

现在解决了。偶数的情况。还得考虑奇数的。奇数的情况下 dp 需要考虑 \(\lceil\frac{m}{2}\rceil\) 轮。对应的，需要在图上走 \(\lceil\frac{m}{2}\rceil\) 步。这是容易的，但是会发现结果较大。这是因为形如 \(f_{\lceil\frac{m}{2}\rceil-1,l,r},r=l+1,S_l=S_r\) 的状态，不能用最终生成的回文串的最中间的一个字符去匹配 \(S_l,S_r\) 两个字符。

接下来的容斥我比较蠢理解了挺久 /wq。要除去多余的情况，首先要注意 dp 在 DAG 上的路径最终必定为走到一红点再走到结束状态（因为无论是剩下一个字符未匹配或两个的情况均对应红点）。所以若经过了 \(x\) 个蓝点，\(|S|-x\) 为奇数的话，那么最终走到的最后一个红点必定对应着一个 \(S:[i,i+1]\) 未匹配的情况。要除去的部分是剩余 \(S:[i,i+1]\) 未匹配且在最后一轮走到结束状态的情况，所以只需求出走 \(\lceil\frac{m}{2}\rceil-1\) 步且停留在最后一个红点的情况数即可。也就是还需要求出矩阵的 \(\lceil\frac{m}{2}\rceil-1\) 次方。

哦忘记这题还卡常了。上文提到经过 \(x\) 个蓝点，红点个数为 \(y=\lceil\frac{n-x}{2}\rceil \le \lceil\frac{n}{2}\rceil\)。所以红点只用建 \(\lceil\frac{n}{2}\rceil\) 个就行了，还有就是对于每条边都 \((u,v)\)，建图时都使 \(u\le v\) 就能使矩阵成为上三角矩阵，有 \(\frac{1}{6}\) 常数。

代码建的图与参考题解的相同。

#include<bits/stdc++.h>
#define fin(x) freopen(#x".in","r",stdin)
#define fout(x) freopen(#x".out","w",stdout)
#define fr(x) fin(x),fout(x);
#define Fr(x,y) fin(x),fout(y)
#define INPUT(_1,_2,FILE,...) FILE
#define IO(...) INPUT(__VA_ARGS__,Fr,fr)(__VA_ARGS__)
using namespace std;
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define cfast ios::sync_with_stdio(false);cin.tie(0),cout.tie(0)
#define ll long long
#define ull unsigned long long
#define intz(x,y) memset((x),(y),sizeof((x)))
char *p1,*p2,buf[100000];
#define nc() (p1==p2 && (p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
inline ll read(){
    ll x=0,f=1;char ch=nc();
    while(ch<48||ch>57){if(ch=='-')f=-1;ch=nc();}
    while(ch>=48&&ch<=57)x=x*10+ch-48,ch=nc();
   	return x*f;
}
void write(int x){cout<<x<<' ';}
void write(pii x){cout<<"P("<<x.fi<<','<<x.se<<")\n";}
void write(vector<auto>x){for(auto i:x)write(i);cout<<'\n';}
inline ll lowbit(ll x){return x&-x;}
inline int pcount(ll x){
	for(int i=0,res=0;;res+=(x>>i)&1,i++)
		if(i>60)return res;
}
#define int ll
const int N=205,M=605,mod=1e4+7;
int n,id[N][3],tot,len,m,f[N][N][N];char s[N];
struct matrix{
	int w[M][M];
	matrix(){intz(w,0);}
	inline void init(){for(int i=1;i<=tot;i++)w[i][i]=1;}
	inline matrix operator*(const matrix x){
		matrix res;
		for(int i=1;i<=tot;i++)
			for(int j=i;j<=tot;j++)
				for(int k=j;k<=tot;k++)
					(res.w[i][k]+=w[i][j]*x.w[j][k]%mod)%=mod;
		return res;
	}
	void print(){
		for(int i=1;i<=tot;i++,cout<<'\n')
			for(int j=1;j<=tot;j++)cout<<w[i][j]<<' ';
	}
	inline matrix qp(matrix x,int y){
		matrix res;res.init();
		while(y){
			if(y&1)res=res*x;
			x=x*x,y>>=1;
		}return res;
	}
	inline void upd(int x,int y,int v){(w[x][y]+=v)%=mod;}
}w,A,B;
int get(int l,int r,int k){
	if(k<0)return 0;
	if(f[l][r][k]!=-1)return f[l][r][k];
	if(l>r)return (k==0);int ans=0;
	if(s[l]==s[r])ans=get(l+1,r-1,k);
	else ans=(get(l+1,r,k-1)+get(l,r-1,k-1))%mod;
	return (f[l][r][k]=ans);
}
inline void UesugiErii(){
	cin>>s>>m;n=strlen(s),m+=n;
	for(int i=n;i;i--)s[i]=s[i-1];s[0]=' ';//0-26,1-25,2-24
	for(int i=(n+1)/2;i;i--){
		id[i][0]=++tot,id[i][1]=++tot;
		w.upd(id[i][0],id[i][1],1),
		w.upd(id[i][1],id[i][1],25);
		if(i<(n+1)/2)w.upd(id[i+1][1],id[i][1],1);
	}
	id[0][0]=++tot;
	w.upd(id[1][1],id[0][0],1);
	for(int i=1;i<=n;i++){
		id[i][2]=++tot;
		w.upd(id[i][2],id[i][2],24);
		if(i>1)w.upd(id[i-1][2],id[i][2],1);
	}
	w.upd(id[1][1],id[1][2],1);
	for(int i=0;i<=(n+1)/2;i++)
		w.upd(id[i][0],id[i][0],26);
	A=w.qp(w,(m+1)/2-1),B=A*w;
	ll sum=0;intz(f,-1);
	for(int i=0;i<=n;i++){
		(sum+=get(1,n,i)*B.w[id[(n-i+1)/2][0]][(i?id[i][2]:id[1][1])]%mod)%=mod;
		if((m&1)&&!((n-i)&1))(sum+=mod-get(1,n,i)*A.w[id[(n-i+1)/2][1]][(i?id[i][2]:id[1][1])]%mod)%=mod;
	}cout<<(sum%mod+mod)%mod;
}
signed main(){
	cfast;
	int _=1;//cin>>_;
	for(;_;_--)UesugiErii();
	return 0;
}