1584. 连接所有点的最小费用

题目：给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

示例 ：

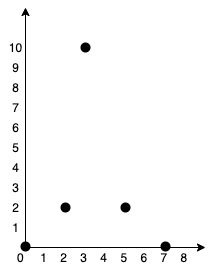
输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
解释：

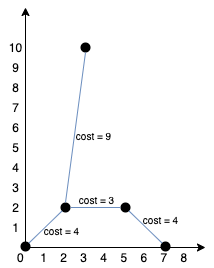
我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。注意到任意两个点之间只有唯一一条路径互相到达。

题解：

class Solution {
public:
    int prim(vector<vector<int> >& points, int start) {
        int n = points.size();
        int res = 0;
        // 1. 计算任意两个point之间的距离
        vector<vector<int> > g(n, vector<int>(n));
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int dist = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1]);
                g[i][j] = dist;
                g[j][i] = dist;
            }
        }
        // 记录V[i]到Vnew的最近距离
        vector<int> lowcost(n, INT_MAX);
        // 记录V[i]是否加入到了Vnew
        vector<int> v(n, -1);

        // 2. 先将start加入到Vnew
        v[start] = 0;
        for (int i = 0; i < n; i++) {
            if (i == start) continue;
            lowcost[i] = g[i][start];
        }

        // 3. 剩余n - 1个节点未加入到Vnew，遍历
        for (int i = 1; i < n; i++) {
            // 找出此时V中，离Vnew最近的点
            int minIdx = -1;
            int minVal = INT_MAX;
            for (int j = 0; j < n; j++) {
                if (v[j] == 0) continue;
                if (lowcost[j] < minVal) {
                    minIdx = j;
                    minVal = lowcost[j];
                }
            }     
            // 将该点加入Vnew，更新lowcost和v
            res += minVal;
            v[minIdx] = 0;
            lowcost[minIdx] = -1;

            // 更新集合V中所有点的lowcost
            for (int j = 0; j < n; j++) {
                if (v[j] == -1 && g[j][minIdx] < lowcost[j]) {
                    lowcost[j] = g[j][minIdx];
                }
            }
        }
        return res;

    }
    int minCostConnectPoints(vector<vector<int>>& points) {
        return prim(points, 0);  
    }
};