DP问题初步
DP初步
记忆化搜索
例题:
AcWing 901.滑雪
#include <bits/stdc++.h>
using namespace std;
const int N=310;
int n,m;
int g[N][N],f[N][N];
int dx[4]={0,1,-1,0},dy[4]={1,0,0,-1};
//这里用递归设置状态
int dp(int x,int y)
{
int &v=f[x][y];
if(v!=-1)return v;
v=1;
for(int i=0;i<4;i++)
{
int a=x+dx[i],b=y+dy[i];
if(a>=1&&a<=n&&b>=1&&b<=m&&g[x][y]>g[a][b])
{
v=max(v,dp(a,b)+1);
}
}
return v;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&g[i][j]);
memset(f,-1,sizeof f);
int res=-1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
res=max(res,dp(i,j));
printf("%d\n",res);
return 0;
}
上升子序列
原始题目描述
给定一个长度为'N'的数列,求数值严格单调递增的子序列的长度最长是多少。
状态转移方程:f[j]=max(f[i],f[j]+1)
#include <bits/stdc++.h>
using namespace std;
const int N=1234;
int f[N],n,a[N];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
{
if(a[j]<a[i])
f[i]=max(f[i],f[j]+1);
}
}
int res=0;
for(int i=1;i<=n;i++)res=max(res,f[i]);
cout<<res;
return 0;
}
例题:
1.怪盗基德的滑翔翼
由题意分析:起点:a[i] 最长距离:以a[i]为起点的最长上升子序列,正反各做一遍
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int f1[N],h1[N],f2[N],h2[N];
int k,n;
int main()
{
cin>>k;
while(k--)
{
memset(f1,0,sizeof f1);
memset(f2,0,sizeof f2);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>h1[i];
h2[n-i+1]=h1[i];
}
for(int i=1;i<=n;i++)
{
f1[i]=1;f2[i]=1;
for(int j=1;j<i;j++)
{
if(h1[i]>h1[j])
f1[i]=max(f1[i],f1[j]+1);
if(h2[i]>h2[j])
f2[i]=max(f2[i],f2[j]+1);
}
}
int res=0;
for(int i=1;i<=n;i++)res=max(f1[i],f2[i]);
cout<<res<<endl;
}
return 0;
}
2.登山
题意分析:
1.按照编号递增的顺序来浏览---->必须是子序列
2.相邻两个景点不能相同-------->严格单调
3.一旦开始下降,就不能上升---->先严格上升,再严格下降
目标:满足上面所有条件的子序列的最大长度
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int f1[N],h1[N],f2[N],h2[N];
int k,n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>h1[i];
h2[n-i+1]=h1[i];
}
for(int i=1;i<=n;i++)
{
f1[i]=1;f2[i]=1;
for(int j=1;j<i;j++)
{
if(h1[i]>h1[j])
f1[i]=max(f1[i],f1[j]+1);
if(h2[i]>h2[j])
f2[i]=max(f2[i],f2[j]+1);
}
}
int res=0;
for(int i=1;i<=n;i++){
res=max(res,f1[i]+f2[n-i+1]-1);
}
cout<<res<<endl;
return 0;
}
3.合唱队形
题意分析:筛出最少的人数使得序列满足条件即从队伍中选出最多的人书满足序列的条件,此题为登山题意的对偶问题
代码只要将登山的输出res改为n-res即可
4.友好城市
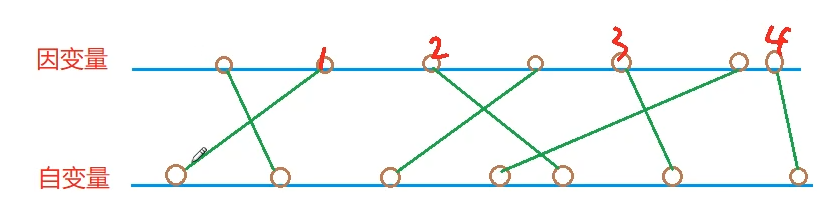
题意分析:对于上面的每一个上升子序列,都匹配一种合理的建桥方式
简单来讲,这题的思路是下面一个有序的序列对应的上序列一定是有序的,如果出现逆序那么一定会交叉
#include <bits/stdc++.h>
using namespace std;
const int N=5010;
typedef pair<int,int>PII;
PII a[N];
int f[N],b[N];
int n;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
a[i].first=x,a[i].second=y;
}
sort(a+1,a+n+1);
for(int i=1;i<=n;i++)
{
b[i]=a[i].second;
}
for(int i=1;i<=n;i++)
{
f[i]=1;
for(int j=1;j<i;j++)
{
if(b[i]>b[j])
{
f[i]=max(f[i],f[j]+1);
}
}
}
int res=0;
for(int i=1;i<=n;i++)res=max(res,f[i]);
cout<<res<<endl;
return 0;
}
5.最大上升子序列的和
题意分析:对模板进行改变,就是将模板中的长度换成数字的和
for(int i=1;i<=n;i++)
{
f[i]=a[i];
for(int j=1;j<i;j++)
{
if(a[j]<a[i])
f[i]=max(f[i],f[j]+a[i]);
}
}
6.拦截导弹
题意分析:
问题1计算这套系统最多能拦截多少导弹:裸的最长上升子序列问题,直接写
问题2如果要拦截所有导弹最少要配备多少套这种导弹拦截系统:贪心(有空写解析)
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int n;
int h[N],f[N],q[N];
int main()
{
string line;
getline(cin,line);
stringstream ssin(line);
while(ssin>>h[n])n++;
int res=0,cnt=0;
for(int i=0;i<n;i++)
{
f[i]=1;
for(int j=0;j<i;j++)
{
if(h[i]<=h[j])
{
f[i]=max(f[i],f[j]+1);
}
}
res=max(res,f[i]);
int k=0;
while(k<cnt&&q[k]<h[i])k++;
if(k==cnt)q[cnt++]=h[i];
else q[k]=h[i];
}
cout<<res<<endl<<cnt<<endl;
return 0;
}
7.导弹防御系统
题意分析:
dfs(u,v,t)意味着当前已经有u个上升,v个下降,正在处理第t个数
#include <bits/stdc++.h>
using namespace std;
const int N=66;
int a[N],ans,up[N],down[N],n;
void dfs(int u,int d,int t)
{
if(u+d>=ans)return;//剪枝,当前的序列数已经大于答案
if(t==n){//当前已经遍历到最后一个点
if(u+d<ans)ans=u+d;
return;
}
int i;
for(i=1;i<=u;i++)if(up[i]<a[t])break;//找到第一个末尾数小于a[t]的导弹系统
int temp=up[i];
up[i]=a[t];//将a[t]添加到该导弹系统中
dfs(max(u,i),d,t+1);
up[i]=temp;//恢复现场
for(i=1;i<=d;i++)if(down[i]>a[t])break;
temp=down[i];
down[i]=a[t];
dfs(u,max(d,i),t+1);
down[i]=temp;
}
int main()
{
while(cin>>n&&n)
{
ans=100;
for(int i=0;i<n;i++)cin>>a[i];
dfs(0,0,0);
printf("%d\n",ans);
}
return 0;
}
8.最长公共上升子序列
题意分析:
状态表示:f [ i , j ]所有由第一个序列的前i个字母,和第二个序列的前j个字母构成的,且以b[j]结尾的公共上升子序列
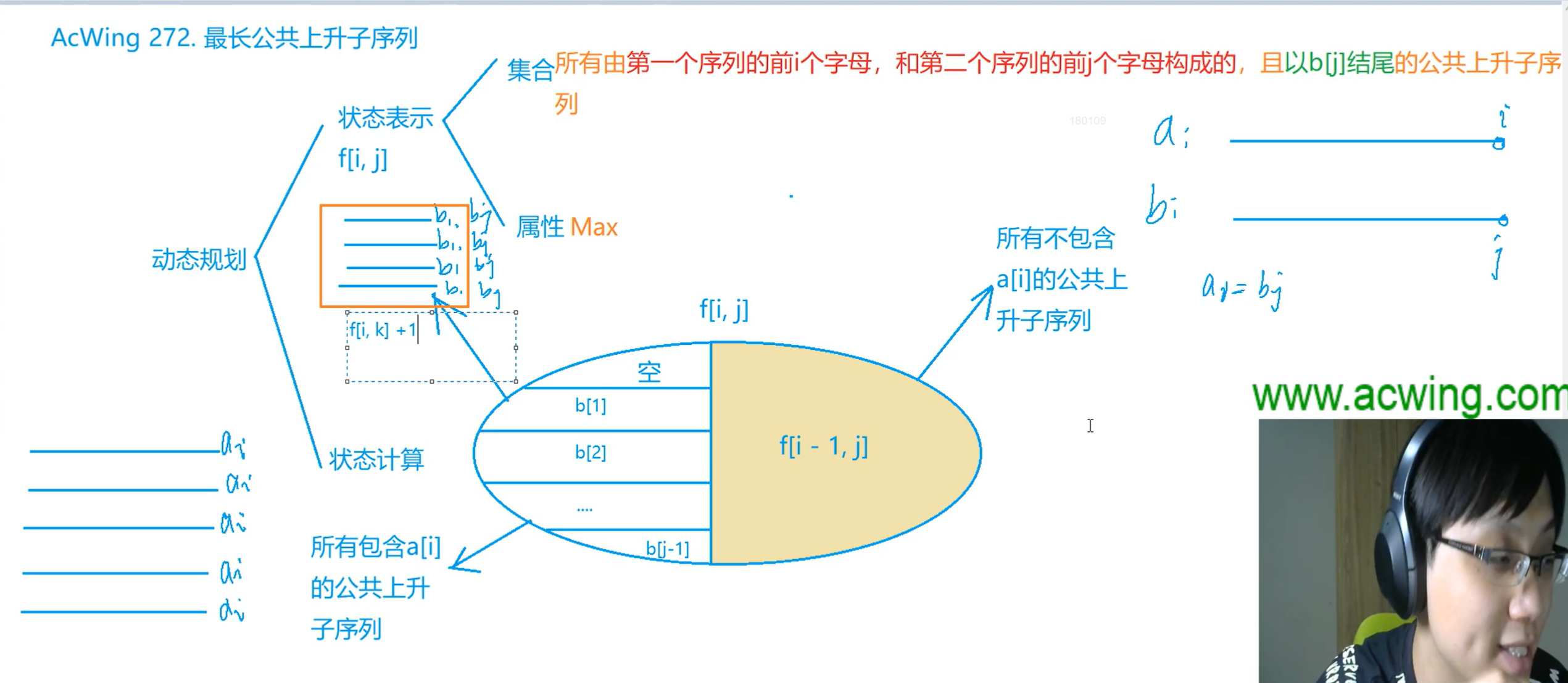
暴力 O(n^3)
#include <bits/stdc++.h>
using namespace std;
const int N=3210;
int n;
int a[N],b[N];
int f[N][N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)scanf("%d",&b[i]);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
f[i][j]=f[i-1][j];
if(a[i]==b[j])
{
f[i][j]=max(f[i][j],1);
for(int k=1;k<j;k++)
if(b[k]<b[j])
f[i][j]=max(f[i][j],f[i][k]+1);
}
}
int res=0;
for(int i=1;i<=n;i++)res=max(res,f[n][i]);
cout<<res<<endl;
return 0;
}
等价优化后O(n^2)
#include <bits/stdc++.h>
using namespace std;
const int N=3210;
int n;
int a[N],b[N];
int f[N][N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)scanf("%d",&b[i]);
for(int i=1;i<=n;i++)
{
int maxv=1;
for(int j=1;j<=n;j++)
{
f[i][j]=f[i-1][j];
if(a[i]==b[j])f[i][j]=max(f[i][j],maxv);
if(b[j]<a[i])maxv=max(maxv,f[i][j]+1);
}
}
int res=0;
for(int i=1;i<=n;i++)res=max(res,f[n][i]);
cout<<res<<endl;
return 0;
}
背包问题
01背包(朴素版)
问题描述: 有N个物品和容量为V的背包,每件物品只能使用一次,第i件物品的体积是vi,价值是wi,求解将这些物品装入背包,使这些物品,体积不超过背包容量,且总价值最大
解题思路
假设子问题的最优解是m(i,j)(物品个数,背包容量)
当前背包容量 j 可选择的物品是 i,i+1.....n
公式:max{m(i+1,j),m(i+1,j-wi)+vi}(j>=wi)
j<wi max{m(i+1,j)} 跳过这个放后面的物品
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int n,m,f[N][N],w[N][N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
f[i][j]=f[i-1][j];
if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
}
return 0;
}
状态机模型
模型简介
例题
1.大盗阿福
题意分析
选择店铺时有两种状态:抢该店铺和不抢该店铺
状态转移方程:f[i]=max(f[i-2]+w[i],f[i-1]) 这个状态转移方程要依赖上两层的状态,在选择第i家时我们不知道i-1家有没有被选
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int w[N],f1[N];
void solve()
{
int n;scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&w[i]);
f1[1]=w[1];
for(int i=2;i<=n;i++)
{
f1[i]=max(f1[i-2]+w[i],f1[i-1]);
}
cout<<f1[n]<<endl;
}
int main()
{
int t;
cin>>t;
while(t--)
{
memset(f1,0,sizeof f1);
solve();
}
return 0;
}
优化的状态表示:f[i,0],f[i,1]:所有走了i步,且当前位于状态j的所有走法
对于f[i,0]:以最后一步进行划分 f[i-1,0] f[i-1,1]
对于f[i,1]:以最后一步进行划分 f[i-1,0]+w[i]
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int w[N],f[N][2];
void solve()
{
int n;scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&w[i]);
for(int i=1;i<=n;i++)
{
f[i][0]=max(f[i-1][0],f[i-1][1]);
f[i][1]=f[i-1][0]+w[i];
}
cout<<max(f[n][1],f[n][0])<<endl;
}
int main()
{
int t;
cin>>t;
while(t--)
{
memset(f,0,sizeof f);
solve();
}
return 0;
}
总结:本题线性DP和状态机都可以做,且两种算法的时间复杂度并没有什么不同,说白了只是状态转移方程两种不同的形式而已
2.股票买卖IV
题意分析
有两个状态:当前手里有股票、当前手里没股票

状态表示为:f[i,j,k]表示 第i天 进行第j次交易 手中是否有股票
1.手中没有股票:f[i-1,j,1]+w[i] f[i-1,j,0]
2.手中有股票:f[i-1,j-1,0]-w[i] f[i-1,j,1]
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int w[N],f[N][110][2];
int main()
{
int n,k;
cin>>n>>k;
for(int i=1;i<=n;i++)scanf("%d",&w[i]);
memset(f,-0x3f,sizeof f);
for(int i=0;i<=n;i++)f[i][0][0]=0;//初始化
for(int i=1;i<=n;i++)
for(int j=1;j<=k;j++)
{
f[i][j][0]=max(f[i-1][j][1]+w[i],f[i-1][j][0]);
f[i][j][1]=max(f[i-1][j-1][0]-w[i],f[i-1][j][1]);
}
int res=0;
for(int i=1;i<=k;i++)res=max({res,f[n][i][1],f[n][i][0]});
cout<<res<<endl;
return 0;
}
3.股票买卖V
题意分析
条件:1.手中只能有一股 2.每股卖出后有一天的冷冻期
三个状态:有股票 没有股票的第一天 没有股票的第>=2天
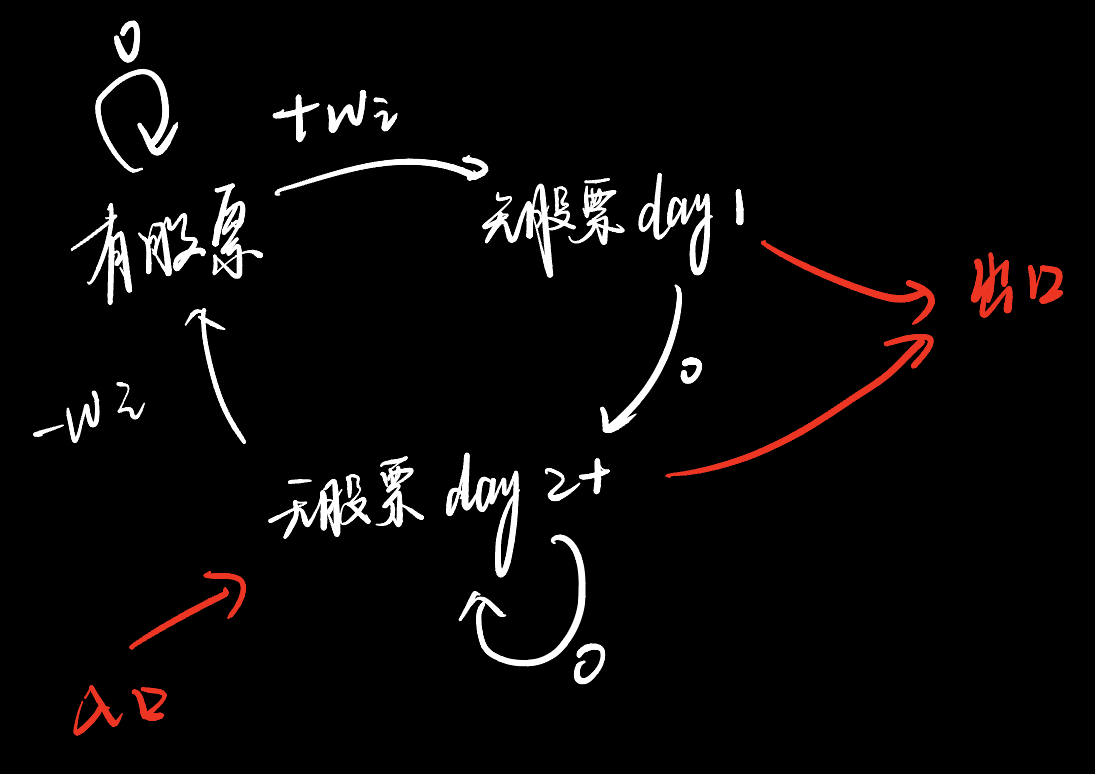
状态表示为:f[i,k] 表示第i天,状态k下的收益
1.有股票:f[i-1,2]-w[i] f[i-1,0]
2.无股票day1:f[i-1,0]+w[i]
3.无股票day2+:f[i-1,1] f[i-1,2]
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10,dinf=-0x3f3f3f3f;
int w[N],f[N][3];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)scanf("%d",&w[i]);
f[0][1]=f[0][0]=dinf;
f[0][2]=0;
for(int i=1;i<=n;i++)
{
f[i][0]=max(f[i-1][2]-w[i],f[i-1][0]);
f[i][1]=f[i-1][0]+w[i];
f[i][2]=max(f[i-1][1],f[i-1][2]);
}
cout<<max(f[n][1],f[n][2])<<endl;
return 0;
}
4.设计密码(*)
题意分析
条件:设计一个密码S满足:
1.S的长度是N
2.S只包含小写的英文字母
3.S不包含字串T
状态表示为:f[i,j] 表示密码已经生成了i位,并且第i位匹配到字符串中的位置为j时的方案数
#include <bits/stdc++.h>
using namespace std;
const int N=55,mod=1e9+7;
int f[N][N],ne[N];
char str[N];//子串
int main()
{
int n,m;
cin>>n>>str+1;
m=strlen(str+1);
for(int i=2,j=0;i<=m;i++)//求出ne数组(kmp模板)
{
while(j&&str[j+1]!=str[i]) j=ne[j];
if(str[j+1]==str[i]) j++;
ne[i]=j;
}
f[0][0]=1;//已经匹配了0位,且匹配的子串的位置是0时的方案数为1;(初始化)
for(int i=0;i<n;i++)//枚举密码位
for(int j=0;j<m;j++)//把第i位密码匹配到的子串位置都枚举一遍
//j表示第i位密码匹配到的位置,因为不能包含子串,所以不能匹配到m这个位置
for(char k='a';k<='z';k++)//把第i+1所有可能的字母都枚举一遍
{
//匹配过程:寻找当第i+1的位置是k时,并且密码已经生成了第i位,匹配的子串的位置是j时,能跳到哪个位置
int u=j;
while(u&&str[u+1]!=k) u=ne[u];
if(str[u+1]==k) u++;
if(u<m) f[i+1][u]=(f[i+1][u]+f[i][j])%mod;
//因为是从f[i][j](i+1的位置为k)跳到f[i+1][u]这个位置,所以f[i+1][u]=f[i+1][u]+f[i][j];
/*
注:可能存在重边,因为j不同但ne[j]是相同的,并且k是相同的,所以此时
f[i][j1]和f[i][j2]跳到的位置是一样的(k相同,ne[j1]=ne[j2])
*/
}
int res=0;
for(int i=0;i<m;i++) res=(res+f[n][i])%mod;
//将所有的方案数加起来即为总方案数
printf("%d",res);
return 0;
}
数位统计DP
模板题:计数问题
刷题
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int
int main()
{
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号