最大流学习笔记

最大流学习笔记

最大流是个毒瘤，我会“详细”记录笔记。

定义

网络，是一张有向图，其上的边权称为容量，即 $ c_{u,v} $。额外地，它拥有一个源点和汇点。

流，就像水流或电流，也具有它们的性质。如果把网络想象成一个自来水管道网络，那流就是其中流动的水。每条边上的流不能超过它的容量，并且对于除了源点和汇点外的所有点（即中继点），流入的流量都等于流出的流量。

网络流的性质如下：

我们不妨设 $ f_{u,v} $ 表示从 $ u $ 到 $ v $ 的最大流。

1. 容量限制：每条边的流量不超过该边的容量，即 $ f_{u,v} \le c_{u,v} $。

2. 斜对称性：每条边的流量与相反边的流量为相反数，即 $ f_{u,v} = -f_{v,u} $。

3. 流量守恒：从源点流出的流量等于汇入汇点的流量，其他中转点，流入和流出量相等。

最大流的定义是：我们有一张图，要求从源点流向汇点的最大流量（可以有很多条路到达汇点）。

Ford-Fulkerson 算法

这个算法的步骤是不断找增广路径，然后计算最大流，最后加起来就行了。

但是如果我们找了一条错误的路径，导致原本的两条路径变成了一条，怎么办？

比如下图：

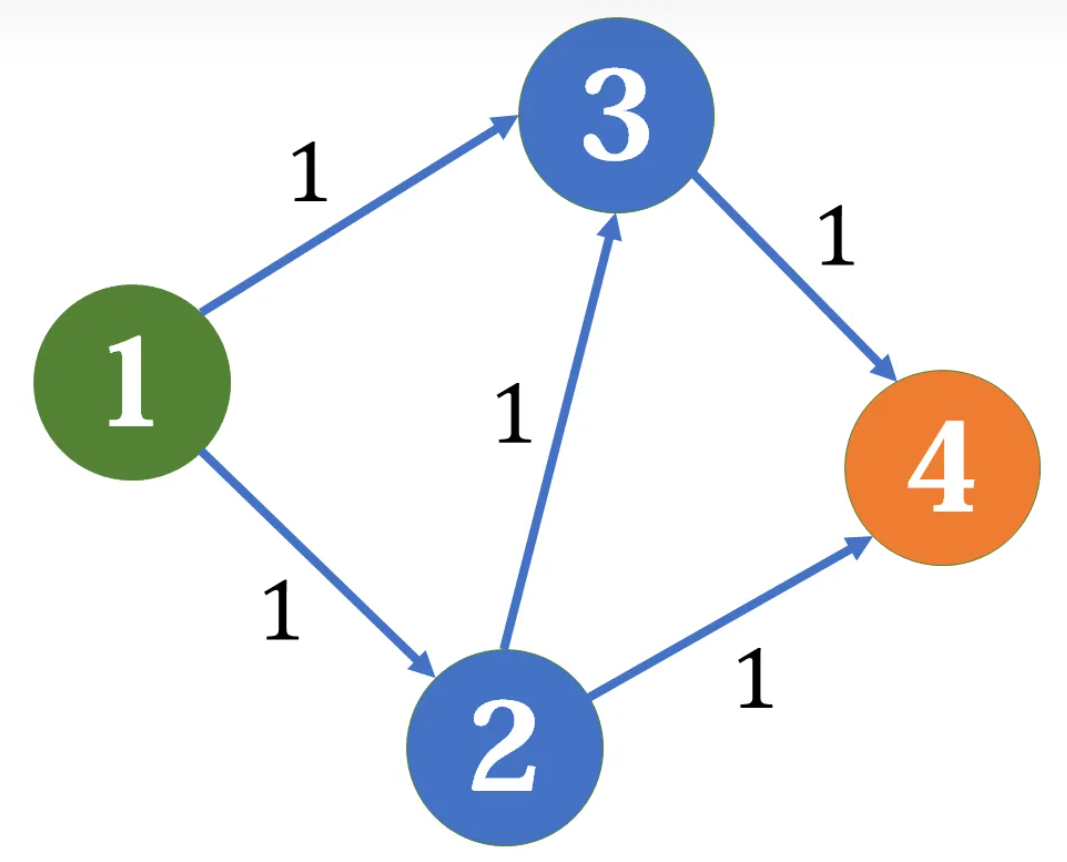
我们找到了一条路径：1 --- 2 --- 3 --- 4。

然后剩下的路径就如下图：

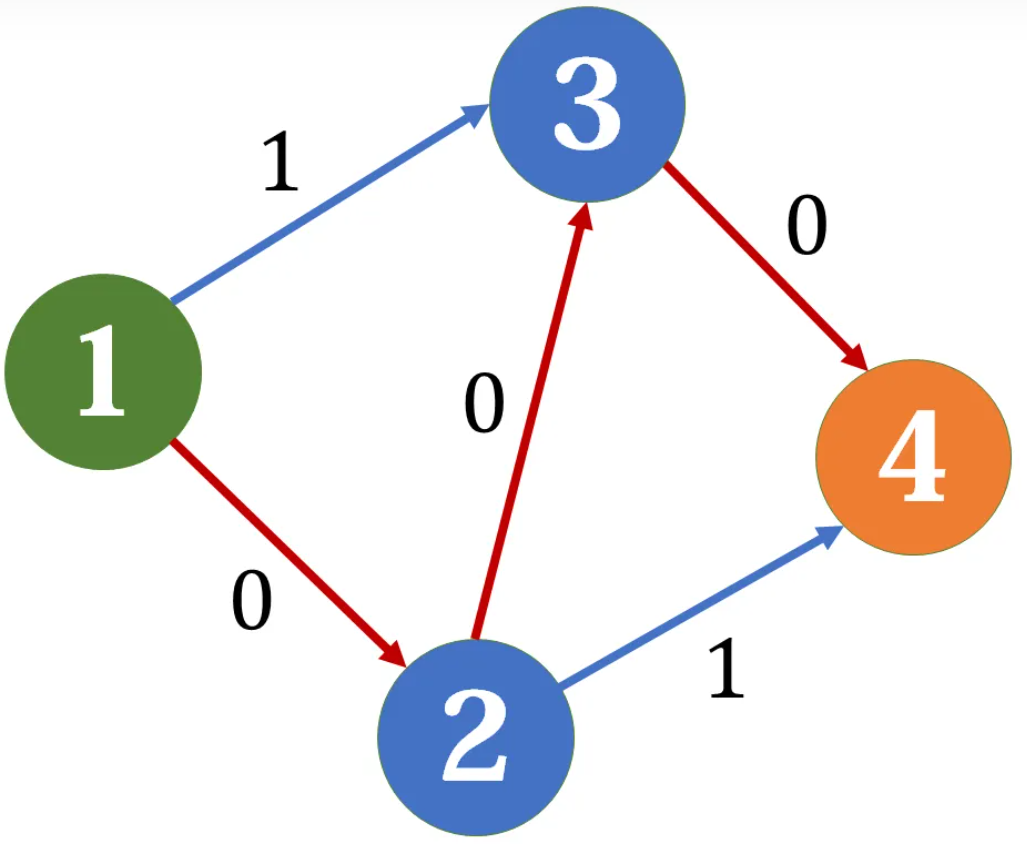
这样算出来的最大流是 $ 1 $，其实实际上最大流是 $ 2 $。这就说明我们的路径找的不对。

我们考虑使用反向路径，我们把正向边减少后在反向边上加上流量，这样我们就可以使用反向路径了。当反向路径被使用的时候，就说明抵消了，也就是这条路径不选了。是不是很好理解？

那最大流就好求了。

Edmond-Karp

这基本就是沿用了 FF 算法。使用 BFS 来找增广路径，然后计算最大流，最后处理反向边。

代码如下：

int n, m;

int G[1005][1005];

int pre[10005]; // 记录路径

int flow[10005]; // 记录最大流

inline int BFS (int s, int t) { // 传入源点和汇点，求增广路径

    for (register int i = 1; i <= n; ++ i) pre[i] = -1;

    flow[s] = 2147483647, pre[s] = 0;

    queue < int > Q;

    Q.push (s);

    while (! Q.empty ()) {

        int u = Q.front ();

        Q.pop ();

        if (u == t) break; // 找到了，退出

        for (register int i = 1; i <= n; ++ i) {

            if (i != s && G[u][i] > 0 && pre[i] == -1) { // 不能回到源点，还有流量，没有访问过

                pre[i] = u;

                Q.push (i);

                flow[i] = min (G[u][i], flow[u]); // 不能超过容量，即容量限制

            }

        }

    }

    if (pre[t] == -1) return -1; // 找不到返回 -1

    else return flow[t]; // 否则返回最大流

}

inline int Edmond_Karp (int s, int t) {

    int Maxflow = 0; // 存储最终答案

    while (1) {

        int flow = BFS (s, t); // 调用 BFS，找一条增广路径

        if (flow == -1) break; // 找不到增广路径就退出

        int cur = t;
        
        while (cur != s) {
            
            int father = pre[cur];

            G[father][cur] -= flow; // 正向边减

            G[cur][father] += flow; // 反向边加

            cur = father;

        }

        Maxflow += flow; // 计算最大流

    }

    return Maxflow;

}