树状数组学习笔记

树状数组学习笔记

基础应用

效果：单点修改+区间查询。

lowbit

首先我们来研究 lowbit。lowbit 是用于求一个数二进制最低位的 $ 1 $ 的位置以及后面的 $ 0 $ 组成的二进制数。比如 $ 6 $ 的二进制是 $ 110 $，所以 lowbit (6) = $ 10 $。

那 lowbit 怎么求呢？这就要考虑关于二进制的补码。二进制的补码就是按位取反再 $ +1 $。那反码的最低位的 $ 0 $，就是原本数最低位的 $ 1 $。那补码就是反码加上 $ 1 $，考虑进位，直到找到最低位的 $ 0 $ 停止进位。那么只有 lowbit 部分是一样的，最后按位与就可以求出 lowbit。所以 lowbit (x) = x & (-x)。

原理

我们考虑用二进制的方式存储。$ c_i $ 存储其二进制内所有为 $ 1 $ 的位数代表的数字。其实就是 lowbit。举个例子：$ c_7 $，$ 7 $ 的二进制是 $ 111 $，然后它有三位是 $ 1 $，最低位代表 $ 1 $，其次是 $ 2 $，然后是 $ 4 $。其实就是用二的幂去拼数，这里用二进制快速解决。所以 $ c_7 = a_1 + a_2 + a_4 $。那我们想要求 $ 1 $ 到 $ n $ 的前缀和，我们考虑把 $ n $ 按刚刚的方式拆分，然后不断加上对应的 $ c $ 数组即可。比如说 $ n=7 $，我们把 $ n $ 拆分成 $ 1,2,4 $，所以我们开始减，每次减去自己的 lowbit 值，也就是分别减 $ 1,2,4 $。也就是说，$ 1 $ 到 $ 7 $ 的前缀和就是 $ c_4 + c_6 + c_7 $。

具体存储方式见下图：

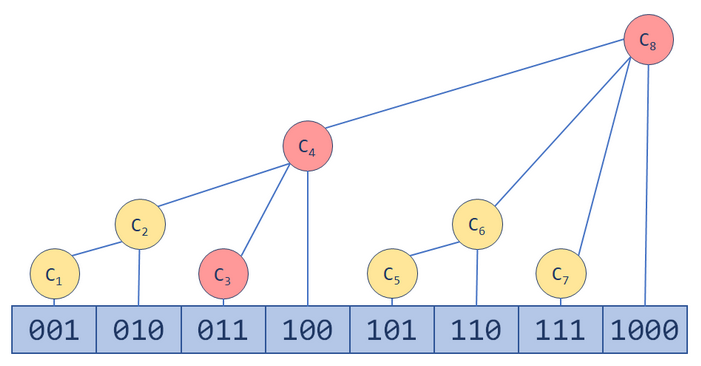
初始化

我们要初始化 $ c $ 数组。

inline void init () {

    for (int i = 1; i <= n; ++ i) c[i] = 0;

}

修改操作

由于修改一个数组的元素，知会影响到后面的数组，我们不放每次加上自己的 lowbit 值。

inline void add (int x, int y) {

    for (int i = x; i <= n; i += lowbit (i)) c[i] += y;

}

于是，我们再输入原始数组的时候，调用 $ add $ 函数就可以了。

查询区间和

我们按照刚刚说的，代码如下：

inline int sum (int x) {

    int ret = 0;

    for (int i = x; i; i -= lowbit (i)) ret += c[i];

    return ret;

}

以上就是树状数组的全部基础应用。下面是更高级的。

进阶应用

效果：区间修改+单点查询。

原理

我们只需要修改一下存储内容。这里我们使用查分树状数组，我们存储的内容是 $ a_i-a_{i-1} $。

简单修改一下代码即可。其他的函数不需要进行修改。