P4479 [BJWC2018] 第k大斜率

Solution

前置芝士：二分，树状数组。

如果要直接统计第 \(k\) 大斜率的值是比较难统计的，可以考虑二分斜率，即要求最大的 \(x\)，满足斜率大于等于 \(x\) 直线数量要大于等于 \(k\)。

对于二分到的一个斜率 \(mid\)，需要考虑如何求直线斜率大于等于它的数量。我们可以枚举一个点，统计以它为直线一端且斜率大于等于 \(mid\) 的数量。

从几何意义上理解这个问题：

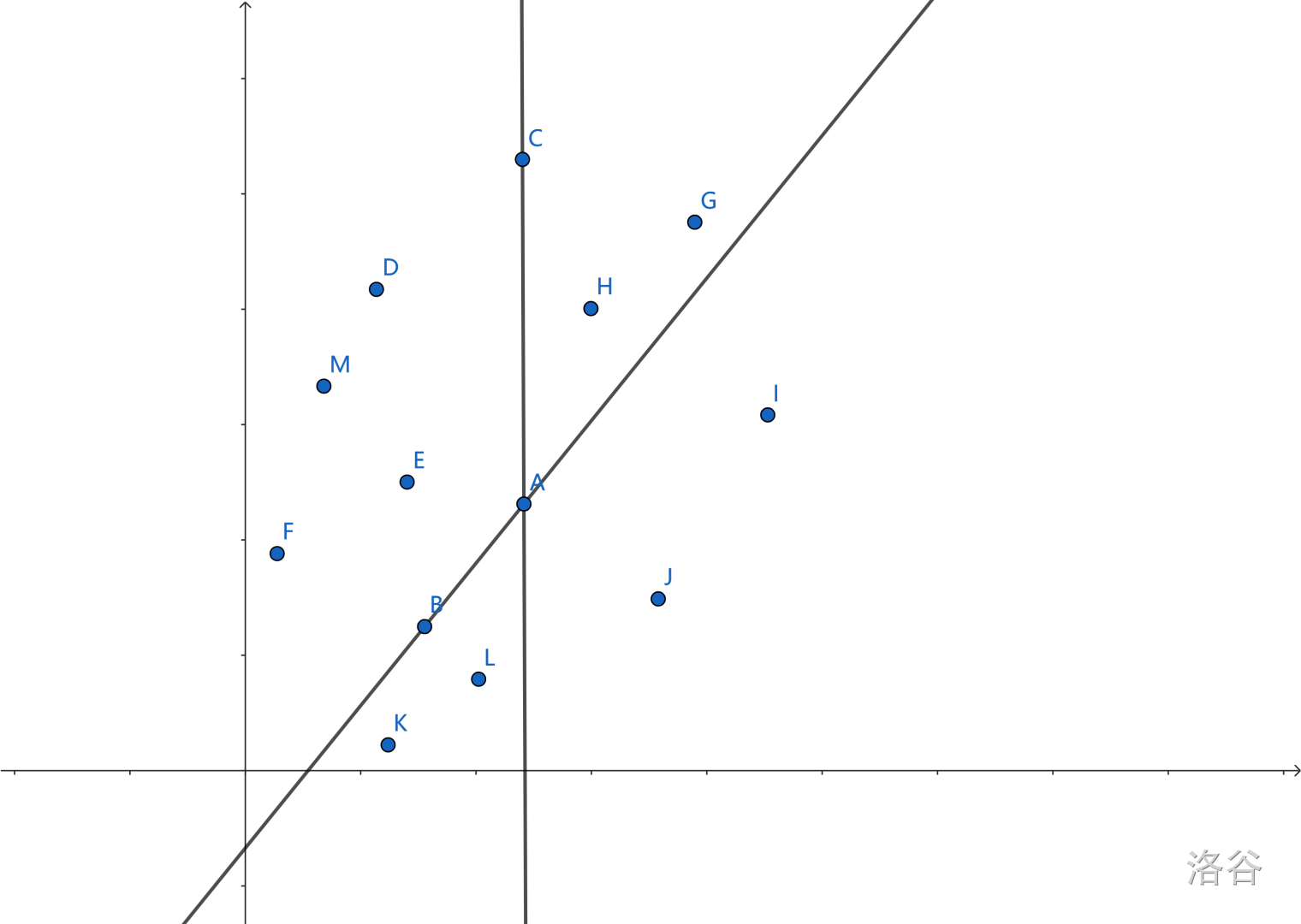
竖线是过 \(A\) 且平行于 \(y\) 轴的直线。若枚举到的点为 \(A\)，那么会发现 \(A\) 与 \(B,G,H,K,L\) 所构成的直线的斜率要大于等于 \(mid\)。

因此，若点在两条直线所切割成平面的左下或右上部分，则这个点与枚举的点所构成的斜率大于等于 \(mid\)。

但如何统计这些点的数量？其实挺简单的。考虑如何判断一个点在直线 \(l_0:y_0=mid \times x+b_0\) 的下方。设过这个点斜率为 \(mid\) 的直线为 \(l_i:y_i=mid \times x+b_i\)，那么要求直线 \(l_i\) 在直线 \(l_0\) 下方，即 \(b_i\le b_0\)。

对于固定的斜率，每个点所在直线的 \(b\) 是可以计算的。因此我们可以按 \(x\) 坐标排序，做一个计算逆序对的方法。具体操作：

1. 计算每一个点的 \(b\)，再离散化
2. 枚举每一个点，用树状数组统计前面有多少个点的 \(b\) 小于等于这个。
3. 将这个点加入树状数组。

左上方也是同理，即统计后面有多少个点在直线上面。

因为线段的两个端点都会被计算一次，因此计算出来的总和要除 \(2\)。

注意：会存在平行于 \(y\) 轴的直线，排序时对于相同的 \(x\) 要按 \(y\) 从大到小排，不然会多算。

Code

#include<bits/stdc++.h>
#define IOS cin.tie(0),cout.tie(0),ios::sync_with_stdio(0)
#define ll long long
#define db double
#define pb push_back
#define eb emplace_back
#define MS(x,y) memset(x,y,sizeof x)
#define MC(x,y) memcpy(x,y,sizeof x)
#define PLL pair<ll,ll>
#define lb(x) (x&-x)
using namespace std;
const int N=1e5+5,M=1e5+5;
const ll INF=1ll<<60,mod=998244353;
int n;
ll k,b[N];
struct point{
	int x,y;
}a[N];
struct BIT{//树状数组 
	int s[N];
	void clear(){
		MS(s,0);
	}
	void add(int x,int d){
		for(;x<=n;x+=lb(x)) s[x]+=d;
	}
	int query(int x){
		int ans=0;
		for(;x;x-=lb(x)) ans+=s[x];
		return ans;
	}
}bit;
vector<ll> z;
void lis(vector<ll> &xx){//离散化 
	sort(xx.begin(),xx.end());
	xx.erase(unique(xx.begin(),xx.end()),xx.end());
}
void getid(vector<ll> &xx,ll &d){
	d=lower_bound(xx.begin(),xx.end(),d)-xx.begin()+1;
}
bool check(int mid){
	bit.clear();z.clear();
	ll sum=0;
	for(int i=1;i<=n;i++){
		b[i]=1ll*a[i].y-1ll*mid*a[i].x;
		z.pb(b[i]);
	}
	lis(z);
	for(int i=1;i<=n;i++) getid(z,b[i]);
	for(int i=1;i<=n;i++) sum+=bit.query(b[i]),bit.add(b[i],1);//右下 
	bit.clear();
	for(int i=1;i<=n;i++) b[i]=z.size()-b[i]+1;
	for(int i=n;i;i--) sum+=bit.query(b[i]),bit.add(b[i],1);//左上 
	return sum/2<k;//要除 2 
} 
int main(){
	IOS;cin>>n>>k;
	for(int i=1;i<=n;i++) cin>>a[i].x>>a[i].y;
	sort(a+1,a+1+n,[&](const point xx,const point yy){
		if(xx.x^yy.x) return xx.x<yy.x;
		return xx.y>yy.y;// y 从大到小排
	});
	int l=-2e8,r=2e8;
	while(l<r){
		int mid=(l+r+1-((l+r+1)%2+2)%2)/2; //等同于 (r+l+1)/2 向下取整
		if(check(mid)) r=mid-1;
		else l=mid;
	}
	cout<<l<<"\n";
	return 0;
}