强化学习收敛性分析工具-2

Optimal Condition

这一章主要介绍判定某个策略是最优策略的依据. 该引理的简单表述如下:

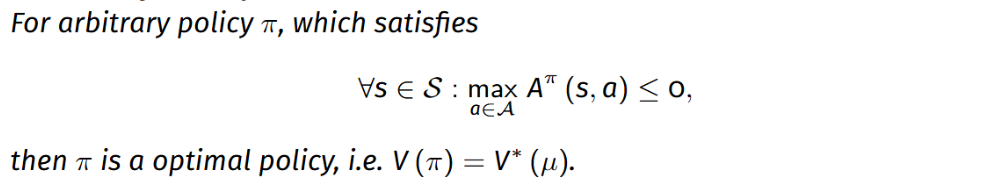
这个定理说明了如果策略 \(\pi\) 的优势函数 \(A\) 处处非正, 那么 \(\pi\) 是最优的, 证明相对简单.

proof

不妨记最优策略为 \(\pi^*\), 记策略 \(\pi\) 满足上述条件:

\[\forall s\in \mathcal{S}:\max_{a\in\mathcal{A}}A^{\pi}(s,a)\leq 0 \]

则

\[\begin{aligned} 0\leq V(\pi^*)-V(\pi)\overset{(i)}{=}\frac{1}{1-\gamma}\mathbb{E}_{s\sim d_{\mu}^{\pi^*}}\mathbb{E}_{a\sim\pi^*(\cdot|s)}[A^{\pi}(s,a)]\leq 0 \end{aligned} \]

\((i)\) 可以通过之前文章中介绍的定理得到, 所以我们有 \(V(\pi^*)=V(\pi)\), 这表明满足上述 Optimal Condition 的 \(\pi\) 也是最优策略. 这就证明了 Optimal Condition 对保证策略最优性的充分性.

同时, Optimal Condition 也是策略最优性的必要条件(这儿默认 \(\forall s\in \mathcal{S}, \mu(s)>0\), 因此 \(\forall\pi,s\in\mathcal{S},d_{\mu}^{\pi}(s)>0\))

proof

设 \(\pi^*\) 是最优策略

假设存在 \(\epsilon>0,s\in \mathcal{S},{a\in\mathcal{A}}\) \(s.t.\) \(A^{\pi^*}(s,a) > \epsilon\), 记这样的 \(s\) 构成集合 \(\mathcal{S}^+\subset\mathcal{S}\) , 构造新的策略

\[\pi'(a|s) = \begin{cases} \frac{\chi_{\{A^{\pi^*} > \epsilon\}}(s,a)}{\displaystyle\sum_{{a\in\mathcal{A}}}\chi_{\{A^{\pi^*} > \epsilon\}}(s,a)} \quad& s\in\mathcal{S}^+\\ \pi^*(a|s) & s \notin \mathcal{S}^+ \end{cases} \]

Then, let

\[\pi(a|s)=\frac{\pi^*({a|s})+\pi'({a|s})}{2} \]

则

\[\begin{cases} \mathbb{E}_{a\sim\pi(\cdot|s)}[A^{\pi^*}(s,a)]>\frac{\epsilon}{2}\quad & s\in\mathcal{S}^+\\ \mathbb{E}_{a\sim\pi(\cdot|s)}[A^{\pi^*}(s,a)] = 0\quad & s\notin\mathcal{S}^+ \end{cases} \]

所以

\[V(\pi)-V(\pi^*)=\frac{1}{1-\gamma}\mathbb{E}_{s\sim d_{\mu}^{\pi}}\mathbb{E}_{a\sim\pi(\cdot|s)}[A^{\pi^*}(s,a)]>0 \]

与 \(\pi^*\) 是最优策略的条件矛盾, 因此假设不成立, 所以若 \(\pi^*\) 是最优策略, 一定满足 Optimal Condition.