【题解】P4220 [WC2018] 通道
题意简述: 给定三棵树 \(T_1,T_2,T_3\),求 \(max\{T_1.dis(a,b)+T_2.dis(a,b)+T_3.dis(a,b)\}\) ,边权为正。
什么??是黑题!!!
先别慌!!!毕竟我连紫题都没做过。
考场上最重要的是什么???是拿分啊!!!
那我们用了什么算法重要吗??不重要!!
我们可以使用一种随机化贪心算法——爬山算法。
这种算法有助于我们在短时间内避开神奇码量,最大化考场得分。
欸那有的人就要问了:到底什么是爬山算法呢??
爬山算法是一种局部择优的方法,采用启发式方法,是对深度优先搜索的一种改进,它利用反馈信息帮助生成解的决策。
直白地讲,就是当目前无法直接到达最优解,但是可以判断两个解哪个更优的时候,根据一些反馈信息生成一个新的可能解。
因此,爬山算法每次在当前找到的最优方案 \(x\) 附近寻找一个新方案。如果这个新的解 \(x'\) 更优,那么转移到 \(x'\) ,否则不变。
是不是感觉有点不太明白?那就不用看明白了,其实就是一种加了随机化的贪心。
那么这道题应该怎么做呢??
我们令 \(dist_{u,v}=dis1_{u,v}+dis2_{u,v}+dis3_{u,v}\) 表示 \(u,v\) 之间的三条路径长度之和。
然后选择一个根 \(a\) ,以这个点为起点在三棵树上分别跑单源最短路,我们就可以得到一个 \(dist_a\) 数组,有一最大值 \(dist_{a,b}\) ,这个节点 \(b\) 即当前根为 \(a\) 的情况下题意中的最远点 \(b\) 。
那么这样就有了一个问题,答案中的这个根到底是谁呢?那么就有了一个想法,我们可以先选择一个点作为初始根,然后用跑到的这个最远点 \(b\) 来继承原来的根。
是的,接下来就不断迭代然后更新最大值就完事了。
然后呢?好像没有了……交一发?

【多么痛的领悟
那么为什么会挂分呢?
记不记得我们前面说到这道题使用的是一种名为爬山算法的随机化算法,但是我们的代码中并没有体现这个随机化。
那我们到底为什么要随机化呢?
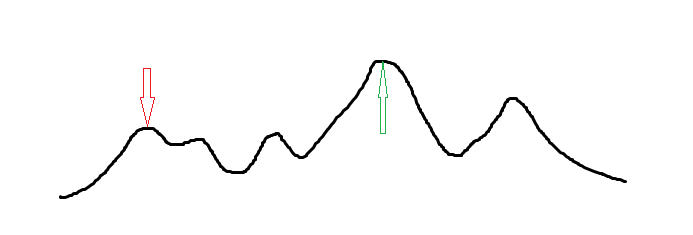
这种贪心对于单峰函数显然是可行的,但如果遇到如图所示的数据,爬山算法很容易陷入一个局部最优解,例如图中的最优解应该为绿色箭头所指的位置,但是爬山算法可能找到的最优解为红色箭头所指的位置。
所以我们考虑使用随机化确定初始根。
但是关键在于我们要随机多少次呢?如何既保证正确,又保证不超时呢?我们需要一个自适应的东西。
这时就要拿出去年上 zhx 的第一节课时学会的一个非常非常实用的东西——时间函数。
是的!我们可以使用卡时大法!!然后就会发现我们成功 AC 了。
代码如下:
#include <bits/stdc++.h>
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 29;
int _, n, m, k, dis[5][N], dist[N], ans, tmp;
bool vis[N];
vector<pii> a[5][N];
void bfs(int s) { // 一个普普通通的 BFS
queue<int> q;
memset(dis, 0, sizeof dis);
for (int g = 1; g <= 3; g++) {
memset(vis, 0, sizeof vis);
q.push(s);
vis[s] = true;
while(q.size()) {
int u = q.front(); q.pop();
for (auto v : a[g][u]) {
if (vis[v.first]) continue;
vis[v.first] = true;
dis[g][v.first] = dis[g][u] + v.second;
q.push(v.first);
}
}
}
}
void tbcsolve() {
cin >> n;
for (int i = 1; i <= 3; i++) {
for (int j = 1; j < n; j++) {
int u, v, w;
cin >> u >> v >> w;
a[i][u].push_back({v, w});
a[i][v].push_back({u, w});
}
}
srand(time(0));
while (clock() < 3.7 * CLOCKS_PER_SEC) { // 卡时大法好!!!
int s = abs(rand()) % n + 1; // 随机化选择初始点
tmp = 0;
int tot = 0;
while (++tot <= n && clock() < 3.7 * CLOCKS_PER_SEC) { // 卡时大法好!!!
bfs(s);
for (int i = 1; i <= n; i++)
dist[i] = dis[1][i] + dis[2][i] + dis[3][i];
for (int j = 1; j <= n; j++) {
if (dist[j] > dist[s]) s = j;
}
if(tmp < dist[s]) tmp = dist[s];
else break;
}
ans = max(ans, tmp); // 迭代更新最大值
}
cout << ans << endl;
}
signed main() {
ios:: sync_with_stdio(0), cin.tie(0), cout.tie(0);
int SHENSELF = 1;
// cin >> SHENSELF;
while (SHENSELF--) tbcsolve();
return 0;
}
感谢 hm2ns 大佬帮我调代码
参考文献



 浙公网安备 33010602011771号
浙公网安备 33010602011771号