[codeforces 804F. Fake bullions]

题目大意：

　　传送门。

　　给一个n个点的有向完全图（即任意两点有且仅有一条有向边）。

　　每一个点上有$S_i$个人，开始时其中有些人有真金块，有些人没有金块。当时刻$i$时，若$u$到$v$有边，若$u$中第$i%S_u$个人有金块（无论真假），且$v$中第$i%S_v$个人没有金块，则会给$v$中第$i%S_v$个人一个假金块。

　　假设这样传递了无数次。（即不会再满足上面的条件时）

　　最后，拥有真金块的人一定可以把金子买出去，而拥有假的人有一半的概率买出去，每买出去一个会给自己的点贡献1的价值。

　　问题是：对于每种所有人卖出金块的结果，卖出最多的前$a$个点中会等概率挑出$b$个点，每个不同的$b$的方案（即存在一个点x在方案一中出现而在方案二中没有出现，称为两个不同的方案）会给答案贡献1,求答案对$1e9+7$的余。

题解：

　　二柱子找到的神题……（它和dp有什么关系……

　　显然我们如果能求出最后每个点有多少假金子这就是一道组合裸体。

　　先不考虑真假。

part1：

　　考虑$u$对$v$的贡献。若u中第x个人有金子，则v中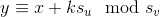的y均会拥有金块，显然 。

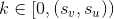　　即所有满足$y \equiv x \mod (s_v,s_u)$的y所有金子。这个推导很简单，把x移到左边然后贝祖定理就完了。

　　即相当与把x映射到$(s_v,s_u)$的剩余系中。我们将其称为$u$对$v$的贡献，用$F(gcd,x)$来表示$u$的元素$x$在$gcd$剩余系下的结果。

　　当$v$又向$w$连边时，我们会发现x对w的贡献是每一个y直接贡献的，即   。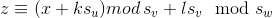

　　类比$x$与$y$的关系我们知道$z\equiv y\mod (s_v,s_w)$。所有有贡献 。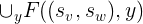

　　再来思考$x$与$z$的关系。有一个显然的结果是$z\equiv x \mod \gcd (s_u,s_v,s_w)$。

　　这个也很好证明：

　　我们知道：设变量$a,b,c,d$满足$c|a,d|b$则会有$(c,d)|a+b$。

　　我们令$c=(s_u,s_v),d=(s_v,s_w),a=x-y,d=y-z$。自然就可以得到这个关系了。

　　同时我们再考虑是否所有满足这个关系的$z$一定会得到金块。

　　即：通过$z$与$x$的关系和$z$与$y$的关系，构造出一个$y$使得能满足$y$与$x$的关系：

　　　　 

　　　　

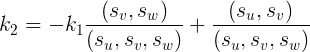
　　这样我们就证明了逆定理的正确性。

　　这用归纳法我们可以证明：设$u$到$v$的一条路径上，设路径上所有点的最大公约数为$gcd$，$u$上$x$对$v$的贡献为$F(gcd,x)$。

part2：

　　可是当出现环呢？

　　我们发现上面的结论时刻成立的，两点间的贡献只和路径$gcd$有关。环内两点的路径可以遍历环内每一个元素，我们会发现最后环里任意两点$gcd$为所有元素最大公约数以后不再变化。那么我们就知道对于环内每个点上的x会对环上所有点产生$F(gcd,x)$的贡献。这样我们用状态$H$来表示在$gcd$的剩余系下都有那些位置被标记过，即$H=\cup_x F(gcd,x)$。

part3：

　　由于这是一个有向完全图，当我们缩点以后，会发现这还是一个有向完全图，不过这次是有向完全DAG。

　　我们已经计算出了缩点后每个环点的状态。

　　考虑在这个有向完全DAG的性质。

　　1.点的出度是递减的。

　　2.点的入度是递增的。

　　3.根据拓扑序遍历我们会得到一条链，且链上点标号递减。

　　以下为缩点后点数为5的例子（由于linux不太会用且校园网有限制只给出有向边，请读者手画一下……）：

　　5->4，5->3，5->2，5->1；4->3，4->2，4->1；3->2，3->1；2->1

　　我们考虑此时环对环的贡献可以转化为$H$间的贡献，其贡献方式与点完全相同。由于缩点以后图的特殊性质，我们如果根据两点之间有边计算贡献无疑会T得飞起。以5对3的贡献为例，一种是5先给4贡献，4在计算此时$H_4$对3的贡献时再把5的贡献传给3,另一种是5对3直接计算贡献。显然我们发现这两种最后的结果都是一样的。那么前者无疑是跟为优秀的，我们按照拓扑后得到的链来传递贡献的话，那么就可以在只枚举一次每个环的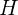计算出所有的贡献。

代码：

　　

#include "bits/stdc++.h"

using namespace std;

inline int read(){
    int s=0,k=1;char ch=getchar();
    while (ch<'0'|ch>'9') ch=='-'?k=-1:0,ch=getchar();
    while (ch>47&ch<='9') s=s*10+(ch^48),ch=getchar();
    return s*k;
}

const int N=5e3+10,M=2e6+10,mod=1e9+7;
typedef long long ll;

struct edges {
    int v;edges *last;  
}edge[N*N],*head[N<<1],*ecnt=edge;

inline void push(int u,int v){
    *ecnt=(edges){v,head[u]},head[u]=ecnt++;
}

inline int powmod(int a,int b){
    int ret=1;
    while (b) {
        if(b&1) ret=(ll)ret*a%mod;
        a=(ll)a*a%mod;
        b>>=1;
    }return ret;
}

inline int gcd(int x,int y){
    return y?gcd(y,x%y):x;
}

int bcc_cnt,bccno[N],stk[N],dfn[N],low[N],idx,top,bgcd[N],s[N],n,a,b,instk[N];

inline void tarjan(int x) {
    low[x]=dfn[x]=++idx;
    stk[++top]=x;
    instk[x]=true;
    for (edges *i=head[x];i;i=i->last)
        if(!dfn[i->v])
            tarjan(i->v),low[x]=min(low[x],low[i->v]);
        else  if(instk[i->v])  low[x]=min(low[x],dfn[i->v]);
    if(dfn[x]==low[x]) {
        bcc_cnt++;int t;
        do instk[t=stk[top--]]=false,bccno[t]=bcc_cnt,bgcd[bcc_cnt]=gcd(bgcd[bcc_cnt],s[t]);while (t!=x);
    }
}

char me[N],gold[M<<1];
int fr[N<<1],in[N],now[N],num[N],mx[N],mn[N];

int inv[N],fac[N];

#define C(i,j) ((ll)fac[(i)]*inv[(j)]%mod*inv[(i)-(j)]%mod)

int  main(){
    //freopen("1.in","r",stdin);
    //freopen("war.out","w",stdout);
    n=read(),a=read(),b=read();
    for (int i=1;i<=n;++i) {
        scanf("%s",me+1);
        for (int j=1;j<=n;++j)  if(me[j]^48)  push(i,j);
    }
    for (int i=1;i<=n;++i)  {
        s[i]=read();
        fr[i]=fr[i-1]+s[i-1];
        scanf("%s",gold+fr[i]);
    }
    for (int i=1;i<=n;++i)  if(!dfn[i])
        tarjan(i);
    bgcd[0]=s[n];
    for (int i=1;i<=bcc_cnt;++i)
        fr[i+n]=fr[i-1+n]+bgcd[i-1];
    fr[n+bcc_cnt+1]=fr[n+bcc_cnt]+bgcd[bcc_cnt];
    for (int i=0;i<fr[n+1];++i)
        gold[i]^=48;
    for (int i=1;i<=n;++i) {
        for (edges *j=head[i];j;j=j->last)  
            if (bccno[i]!=bccno[j->v])
                push(bccno[i]+n,bccno[j->v]+n),++in[bccno[j->v]];
        for (int j=fr[i];j<fr[i+1];++j)
            if (gold[j])    
                gold[fr[bccno[i]+n]+(j-fr[i])%bgcd[bccno[i]]]=true;
    }
    now[bcc_cnt]=bgcd[bcc_cnt];
    for (int i=bcc_cnt;i>1;--i) {
        now[i-1]=gcd(bgcd[i],bgcd[i-1]);
        for (int j=0;j<bgcd[i];++j)    if(gold[fr[i+n]+j])
            ++num[i],gold[fr[i+n-1]+j%now[i-1]]=true;
    }
    for (int j=0;j<bgcd[1];++j) if(gold[fr[1+n]+j])
        ++num[1];
    for (int i=1;i<=n;++i)  {
        mx[i]=(ll)num[bccno[i]]*s[i]/bgcd[bccno[i]];
        for (int j=fr[i];j<fr[i+1];++j)
            mn[i]+=gold[j];
    }
    fac[0]=1;
    for (int i=1;i<=n;++i) fac[i]=(ll)fac[i-1]*i%mod;inv[0]=inv[1]=1;
    for (int i=2;i<=n;++i)  inv[i]=(ll)inv[mod%i]*(mod-mod/i)%mod;
    for (int i=2;i<=n;++i)  inv[i]=(ll)inv[i]*inv[i-1]%mod;
    int ans=0;
    for (int i=1;i<=n;++i) {
        int c1=0,c2=0;
        for (int j=1;j<=n;++j) if (mn[j]>mx[i]) ++c1;
        if (c1>=a) continue;
        for (int j=1;j<=n;++j)  
            if (mn[j]<=mx[i]&&(mx[j]>mx[i]||mx[j]==mx[i]&&j>i)) ++c2;
        for (int j=min(b-1,min(c2,a-1-c1));b-j-1<=c1&&(~j);--j) 
            ans=(ans+C(c2,j)*C(c1,b-j-1)%mod)%mod;
    }
    printf("%d\n",ans);
}