算法

本章节主要介绍了二分查找法、三种低级排序的方法（冒泡排序、选择排序、插入排序）、三种高级排序方法（快速排序、堆排序、归并排序）。

二分查找法

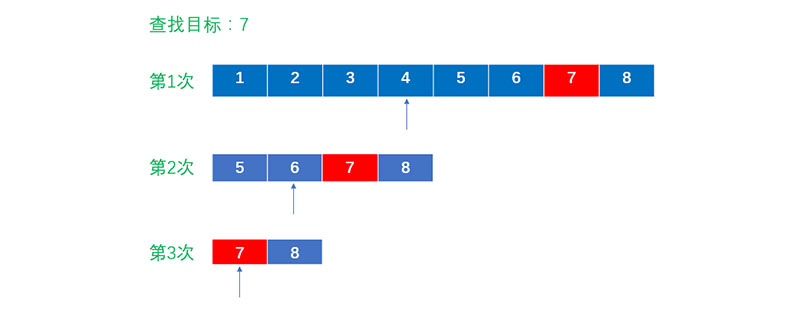
二分查找法是基于此列表是有序的，比如是一个升序。

def binary_search(li, val):
    """
    二分查找法，成功找到值则返回索引，否则返回-1
    :param li:
    :param val:
    :return:
    """
    low = 0
    height = len(li) - 1
    while low <= height:
        mid = (low + height) // 2
        if li[mid] > val:
            height = mid - 1
        elif li[mid] < val:
            low = mid + 1
        else:
            return mid
    else:
        return -1

冒泡排序

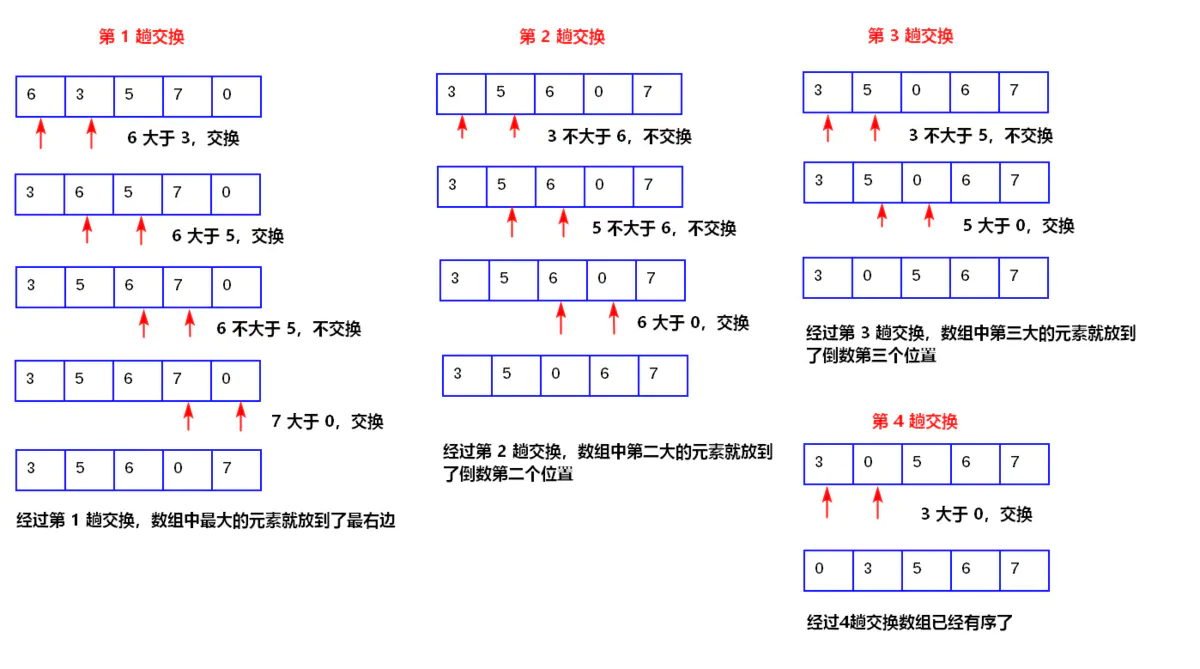
它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。

def bubble_sort(li):
    """
    冒泡排序
    :param li:
    :return:
    """
    for i in range(len(li) - 1):
        # i表示的是第几趟
        for j in range(0, len(li) - i - 1):
            if li[j] > li[j + 1]:
                li[j], li[j + 1] = li[j + 1], li[j]


def bubble_sort2(li):
    """
    冒泡排序改进版，就是一趟没有任何改变，则直接结束
    :param li:
    :return:
    """
    for i in range(len(li) - 1):
        # i表示的是第几趟
        change = False
        for j in range(0, len(li) - i - 1):
            if li[j] > li[j + 1]:
                li[j], li[j + 1] = li[j + 1], li[j]
                change = True
        if not change:
            return

选择排序

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

def select_sort(li):
    for i in range(len(li) - 1):
        min_loc = i  # 最小数位置
        for j in range(i + 1, len(li) - 1):
            if li[j] < li[min_loc]:
                min_loc = j
        li[i], li[min_loc] = li[min_loc], li[i]

插入排序

插入排序的思想：把列表分成有序区和无序区，拿无序区的第一个数，然后把此数放到有序区合适的位置。如此循环，直到无序区没有数。

def insert_sort(li):
    for i in range(1, len(li)):
        # 无序区的第一个数
        tmp = li[i]
        # 有序区的最后一个位置
        j = i - 1
        while li[j] > tmp and j >= 0:
            li[j + 1] = li[j]
            j -= 1
        li[j+1] = tmp

快速排序

快速排序的思想：从列表中取一个元素（一般是第1个），然后遍历列表，使得此元素的左边均比它小，右边的元素均比它大，然后继续通过递归实现排序

def partition(li, left, right):
    """
    此函数用于对于列表li，首先从一个随机位置和第一个位置交换数值，然后把第一个数放到一个位置，此位置的左边
    数值均比它小，右边的数值均比它大，返回此位置的索引
    :param li: 列表
    :param left: 最左边的位置
    :param right: 最右边的位置
    :return: 返回此位置的索引
    """
    # 交换数
    random_index = random.randint(left + 1, right)
    li[left], li[random_index] = li[random_index], li[left]
    tmp = li[left]
    while left < right:
        # 当left=right时，即找到位置时，退出循环
        while left < right and li[right] >= tmp:
            # 当找到比tmp小的数时退出循环
            right -= 1
        li[left] = li[right]
        while left < right and li[left] <= tmp:
            # 当找到比tmp大的数时退出循环
            left += 1
        li[right] = li[left]
    li[left] = tmp
    return left


def _quick_sort(li, left, right):
    if left < right:
        # 表明有起码有两个元素
        mid = partition(li, left, right)
        _quick_sort(li, left, mid - 1)
        _quick_sort(li, mid + 1, right)

堆排序

概念解析：
二叉树：度不超过2的树（节点最多有两个叉）
满二叉树：如果每层的节点数都达到最大值的二叉树
完全二叉树：叶节点只能出现在最下层或是次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树

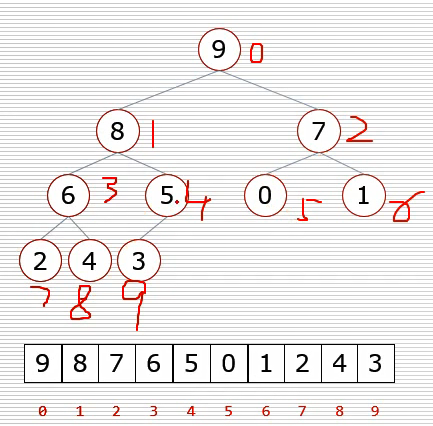
小根堆：满足父亲节点均比孩子节点小的完全二叉树
大根堆：满足父亲节点均比孩子节点大的完全二叉树
向下调整：顶端节点不符合堆的字义，而其左右的子树符合堆的定义，可通过向下调整帮顶端找到合适的位置。

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了
步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。
a.假设给定无序序列结构如下

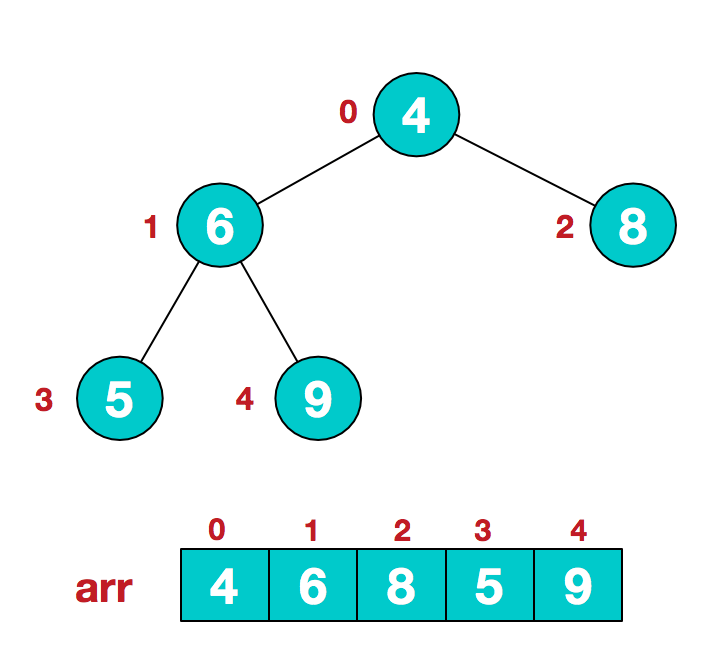
2.此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

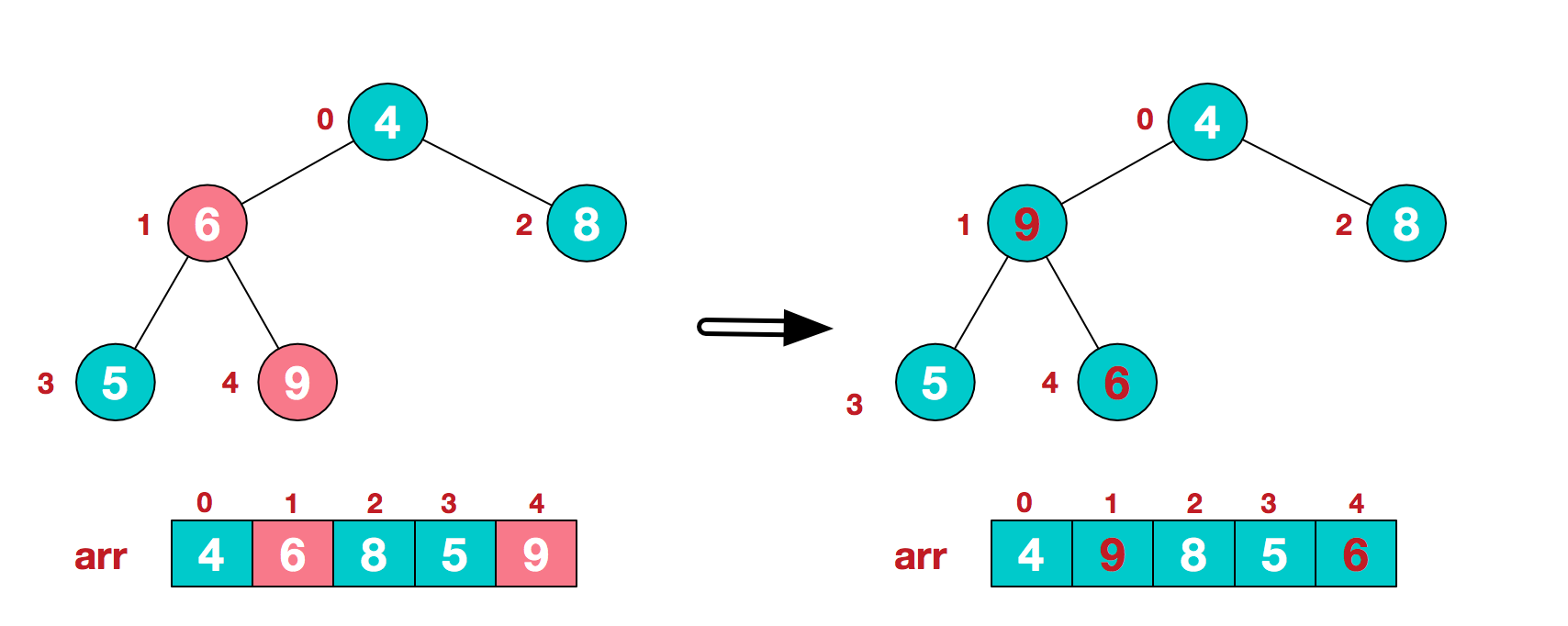
4.找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

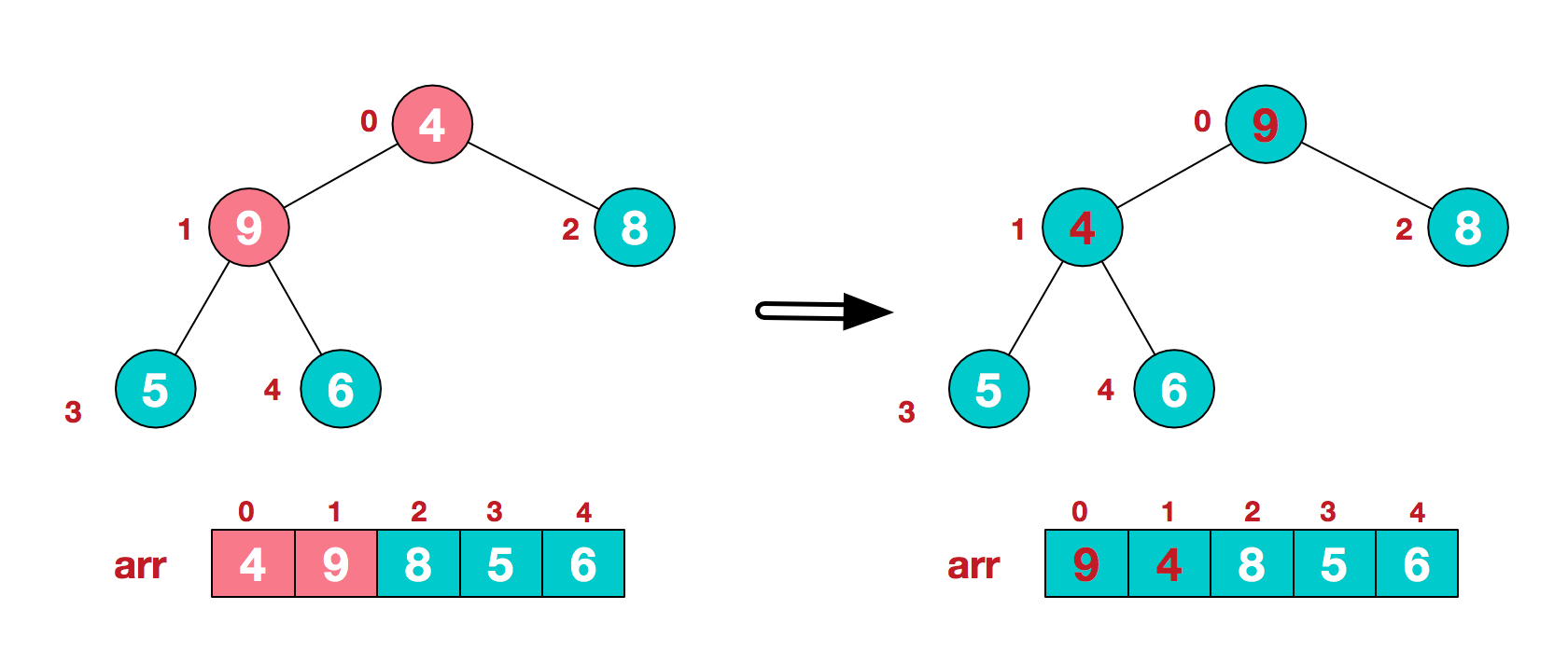
这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

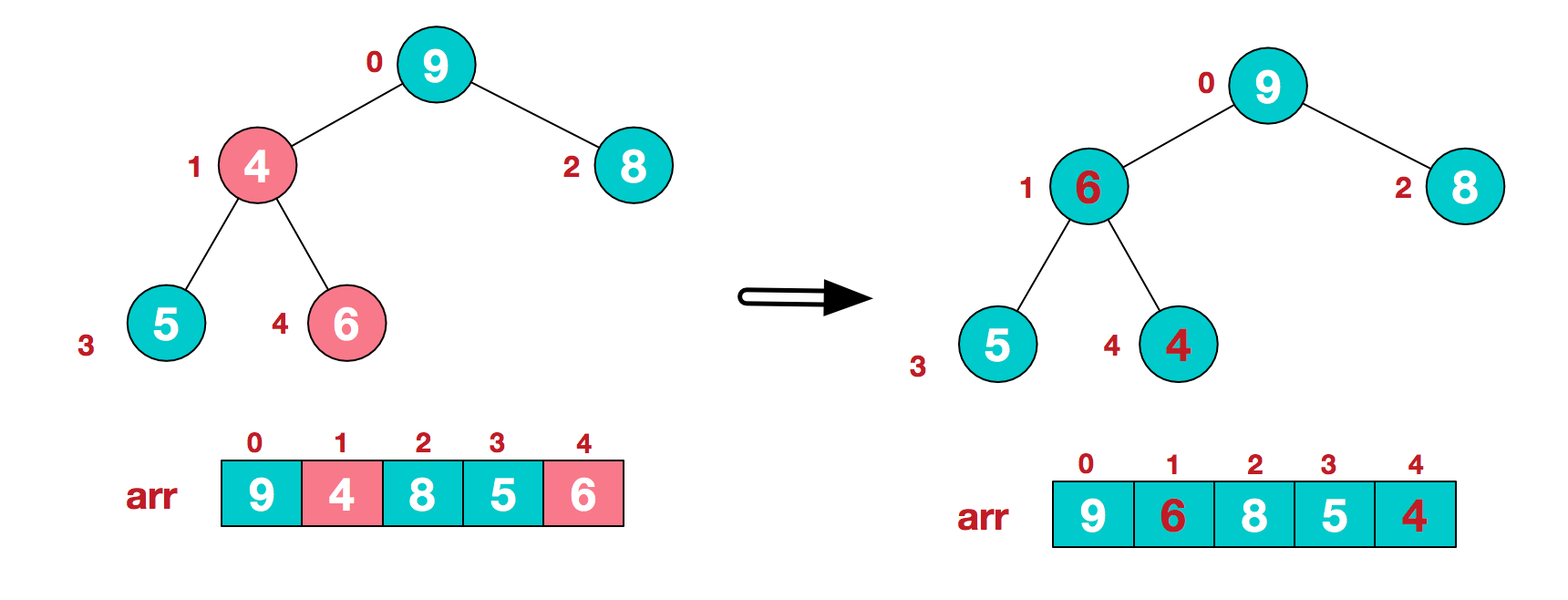
此时，我们就将一个无需序列构造成了一个大顶堆。
步骤二 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。
a.将堆顶元素9和末尾元素4进行交换

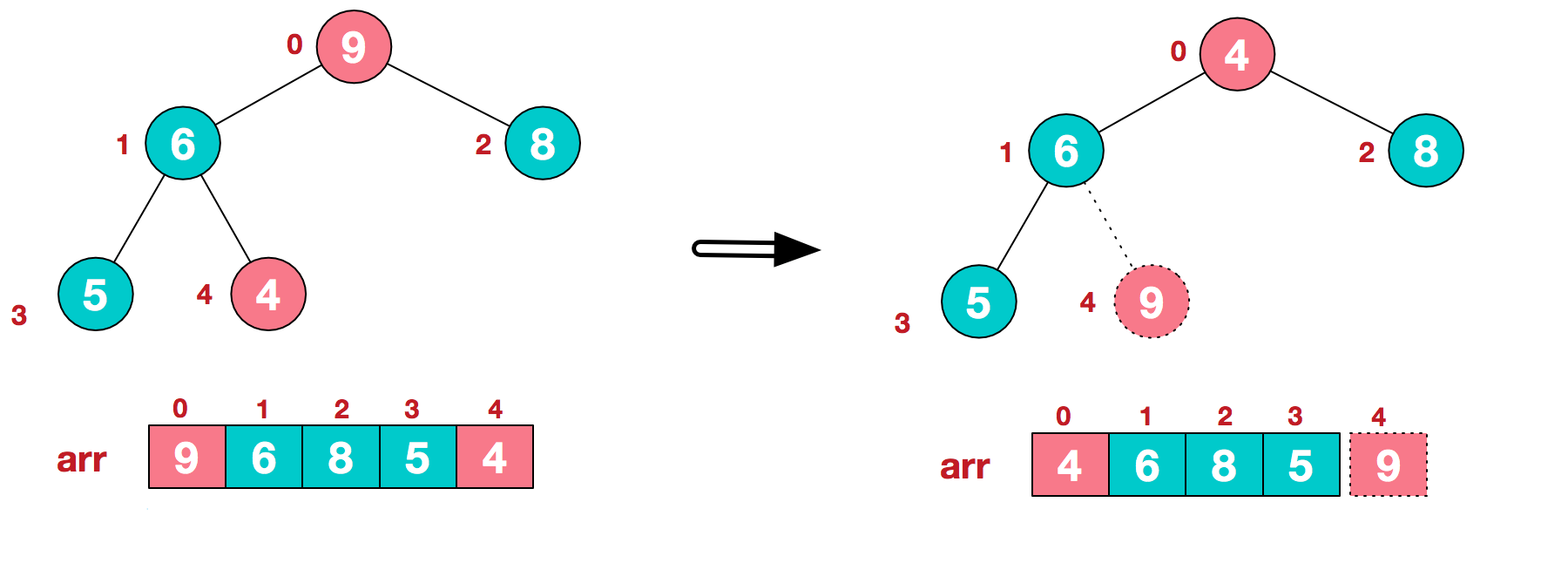
b.重新调整结构，使其继续满足堆定义

c.再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.

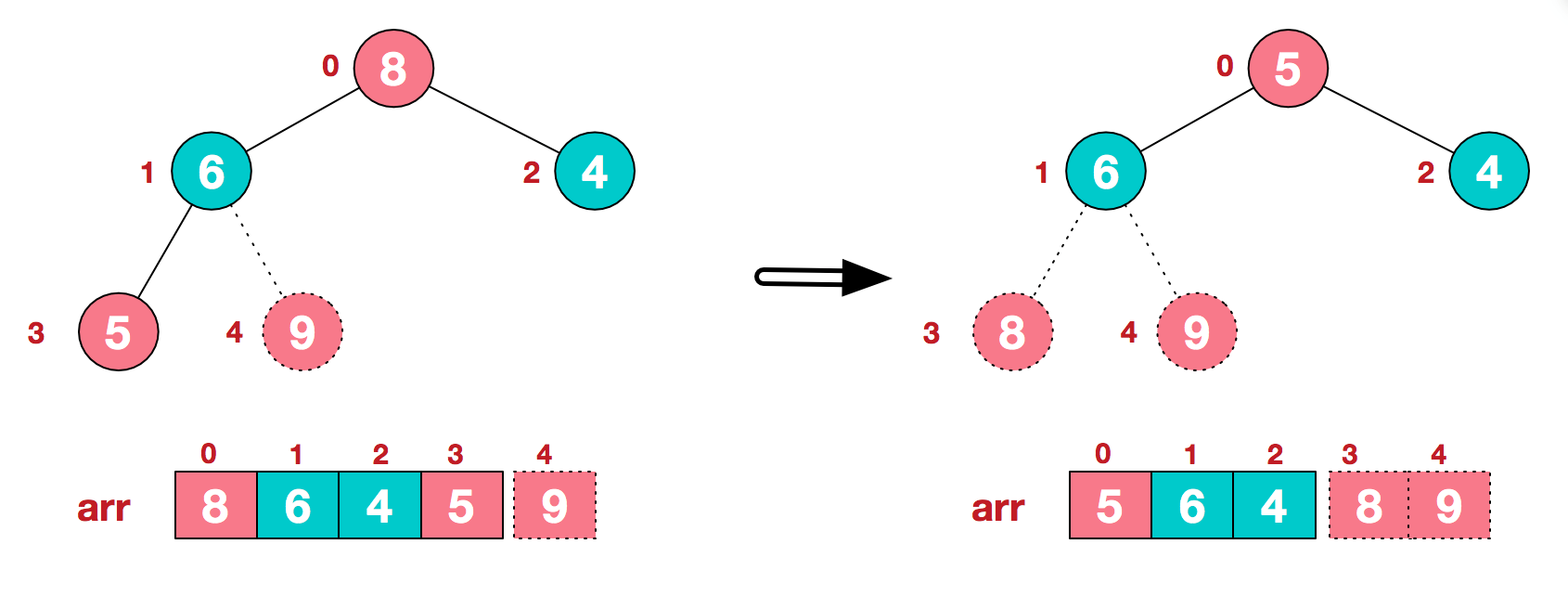
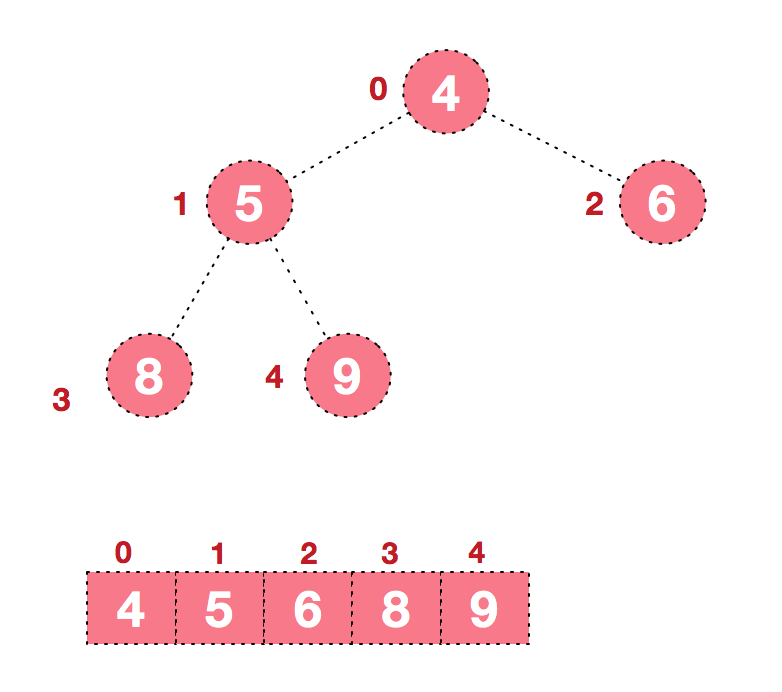
后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

def sift(li, low, high):
    """
    向下调整
    有一个堆，最顶端（省长）不是堆，其左右堆均是堆，现在要调整省长的位置
    :param li: 列表
    :param low: 堆的开始位置
    :param high: 堆的结束位置
    :return:
    """
    tmp = li[low]  # 堆顶端的值
    i = low  # 父亲的位置
    j = 2 * i + 1  # 左孩子的位置
    while j <= high:
        # 如果右孩子存在并且右孩子较大
        if j + 1 <= high and li[j + 1] > li[j]:
            # 把孩子当中较大的给j保存
            j += 1
        # 较大的孩子如果比省长大，则原省长位置就给此孩子
        if tmp < li[j]:
            li[i] = li[j]
            i = j
            j = 2 * i + 1
        else:
            break
    li[i] = tmp



def heap_sort(li):
    """
    对列表li利用堆进行排序，首先建堆，然后挨个数
    :param li:
    :return:
    """
    n = len(li)
    # 第一步、建堆
    for i in range(n // 2 - 1, -1, -1):
        sift(li, i, n - 1)
    # 第二步，挨个出数
    # j表示最后一个元素的位置
    for j in range(n - 1, -1, -1):
        # 交换省长和傀儡的位置，同时元素减1
        li[0], li[j] = li[j], li[0]
        sift(li, 0, j - 1)

利用堆模块排序

import heapq


def heap_sort(li):
    """
    利用heapq模块实现排序功能
    :param li:
    :return:
    """
    # 构造堆
    heapq.heapify(li)
    n = len(li)
    new_li = []
    for i in range(n):
        # heapop每次会从列表获取最小的值
        new_li.append(heapq.heappop(li))
    return new_li

heapq.nlargest(k, li)  # 从列表中获取最大的k个值
heapq.nsmallest(k, li)  # 从列表中获取最小的k个值

归并排序

归并排序是用分治思想，分治模式在每一层递归上有三个步骤：
分解（Divide）：将n个元素分成个含n/2个元素的子序列。
解决（Conquer）：用合并排序法对两个子序列递归的排序。
合并（Combine）：合并两个已排序的子序列已得到排序结果。

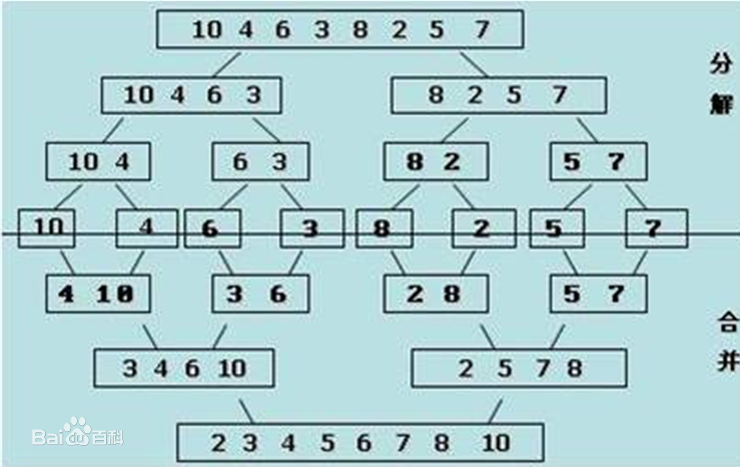
def merge(li, low, mid, high):
    """
    一次归并
    :param li:
    :param low:
    :param mid:
    :param high:
    :return:
    """
    i = low
    j = mid + 1
    l_tmp = []
    # 左右两边的指针都还未遍历完时
    while i <= mid and j <= high:
        if li[i] < li[j]:
            l_tmp.append(li[i])
            i += 1
        else:
            l_tmp.append(li[j])
            j += 1
    while i <= mid:
        l_tmp.append(li[i])
        i += 1
    while j <= high:
        l_tmp.append(li[j])
        j += 1
    li[low:high+1] = l_tmp


def _merge_sort(li, low, high):
    if low < high:
        mid = (low + high) // 2
        _merge_sort(li, low, mid)
        _merge_sort(li, mid+1, high)
        merge(li, low, mid, high)