栈
1、基本概念
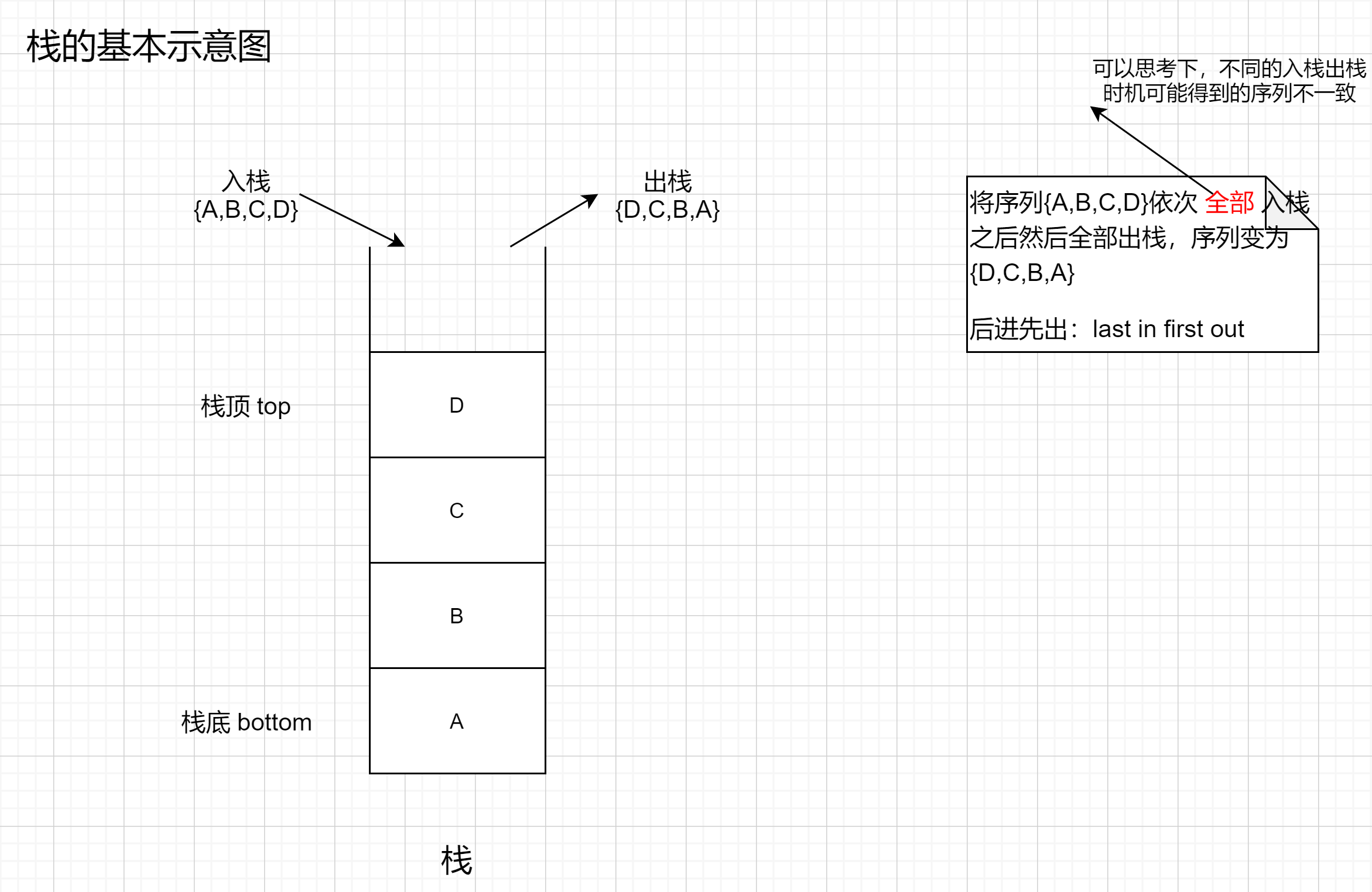
- 栈(stack)是一种特殊的线性表,其插入何删除操作只允许再线性表的一端进行。允许操作的一端成为栈顶(top),不允许操作的一端称为栈底(bottom)。
- 栈中插入元素的操作叫做入栈(push),删除元素的操作叫做出栈(pop)。
- 没有元素的栈成为空栈。
- 后进先出(last in first out):由于栈的插入和删除只允许再一端进行,每次入栈元素即成为当前栈顶元素,每次出栈元素总是最后一个入栈的元素,也被叫做后进先出表。
2、两种实现方式:顺序栈 + 链表栈
存储方式分为两种:开辟一块连续的内存空间顺序存储、链式空间存储
栈基本操作有创建栈、入栈、出栈、取栈顶元素、判断栈是否为空等,其中取栈顶元素仅取元素而不将元素删除。
public interface SStack<T> {
/**
* 判断当前栈是否为空栈
*
* @return boolean true-是空栈、false-不是空栈
*/
boolean isEmpty();
/**
* 元素入栈
*
* @param t 待入栈元素
* @return void
*/
void push(T t);
/**
* 元素出栈
*
* @return T 所出栈的元素
*/
T pop();
/**
* 取出栈顶元素,此时栈顶元素并未出栈
*
* @param
* @return T 栈顶元素
*/
T get();
}
2.1、顺序栈
概念简介:
采用顺序存储结构来实现的栈称之为顺序栈。
核心 API 纵览
具体实现:
/**
* @ClassName SeqStack
* @Description: 顺序栈类:采用顺序存储结构存储数据来实现栈
* @Author: myl
* @Create_time:2021/1/30 16:52
*/
public class SeqStack<T> implements SStack<T> {
/**
* 底层使用数据存储元素
*/
private Object[] element;
/**
* 定义栈顶元素的下标,初始化时设置为 -1
*/
private int top;
/**
* 初始化给定容量的栈容器
*
* @param size
* 指定的栈容器容量大小
*/
public SeqStack(int size) {
this.element = new Object[Math.abs(size)];
this.top = -1;
}
/**
* 默认构造器中容量大小设置为64
*/
public SeqStack() {
this(64);
}
/**
* 判断当前栈是否为空栈
* <p>
* 初始化容器时指定栈顶元素下标为 -1,所以直接通过当前栈顶元素下标是否为 -1 来判断当前栈容器是否为空。所以要求在入栈和出栈时维护栈顶元素下标值
* </p>
*
* @return boolean true-是空栈、false-不是空栈
*/
@Override
public boolean isEmpty() {
return top == -1;
}
/**
* 元素入栈
*
* @param t
* 待入栈元素
* @return void
*/
@Override
public void push(T t) {
if (Objects.isNull(t)) {
return;
}
// 先判断当前栈是否已满,如果栈已满,则需要申请一个更大的空间存储栈元素,所以创建栈时如果知道数据量直接声明其大小
if (top == element.length) {
Object[] temp = this.element;
this.element = new Object[temp.length * 2];
// 将原来数组中数据拷贝
for (int i = 0; i < temp.length; i++) {
element[i] = temp[i];
}
}
// 栈顶元素下标维护并将元素入栈
element[++top] = t;
}
/**
* 元素出栈
*
* @return T 所出栈的元素
*/
@Override
public T pop() {
// 先行判断栈是否为空
if (top == -1){
throw new RuntimeException("当前栈中无可出栈的元素");
}
// 栈顶出栈:取出栈顶元素,并维护栈顶元素
return (T)element[top--];
}
/**
* 取出栈顶元素,此时栈顶元素并未出栈
*
* @return T 栈顶元素
*/
@Override
public T get() {
// 先行判断栈是否为空
if (top == -1){
throw new RuntimeException("当前栈中无元素可获取");
}
// 取出栈顶元素
return (T)element[top];
}
public int size(){
return element.length;
}
}
2.2、链式栈
概念简介
采用链式存储结构存储数据的方式实现的栈称为链式栈。
核心 API 纵览
具体实现
/**
* 链式表中使用的节点对象:指向下一个的地址和存储的元素值
*
* @param <T>
*/
class Node<T> {
/**
* 指向下一个节点
*/
Node<T> next;
/**
* 存储实际数据值
*/
T data;
public Node(Node<T> node, T data) {
this.next = node;
this.data = data;
}
public Node() {}
}
/**
* @ClassName LinkedStack
* @Description: 链表式栈:采用链式存储结构存储数据来实现栈
* @Author: myl
* @Create_time:2021/1/30 16:52
*/
public class LinkedStack<T> implements SStack<T> {
/**
* 定义栈顶元素
*/
private Node<T> top;
public LinkedStack(Node<T> node) {
this.top = node;
}
public LinkedStack() {}
/**
* 判断当前栈是否为空栈
*
* @return boolean true-是空栈、false-不是空栈
*/
@Override
public boolean isEmpty() {
return top == null;
}
/**
* 元素入栈:构建新节点,其next指向原top对象,后将top指向新节点对象
*
* @param t
* 待入栈元素
* @return void
*/
@Override
public void push(T t) {
if (t == null) {
throw new RuntimeException("入栈元素不可为null");
}
this.top = new Node<>(top, t);
}
/**
* 元素出栈
*
* @return T 所出栈的元素
*/
@Override
public T pop() {
// 将 top 指向的节点置为 top ,当前 top 置为null
if (top == null) {
throw new RuntimeException("当前无元素可出栈");
}
Node<T> temp = top;
top = top.next;
return temp.data;
}
/**
* 取出栈顶元素,此时栈顶元素并未出栈
*
* @return T 栈顶元素
*/
@Override
public T get() {
return top == null ? null : top.data;
}
}
3、栈实战
适用情景:
任何使用 后入先出 这种数据结构的地方都适合使用栈结构(好像是废话,只能简化总结成这样了)。
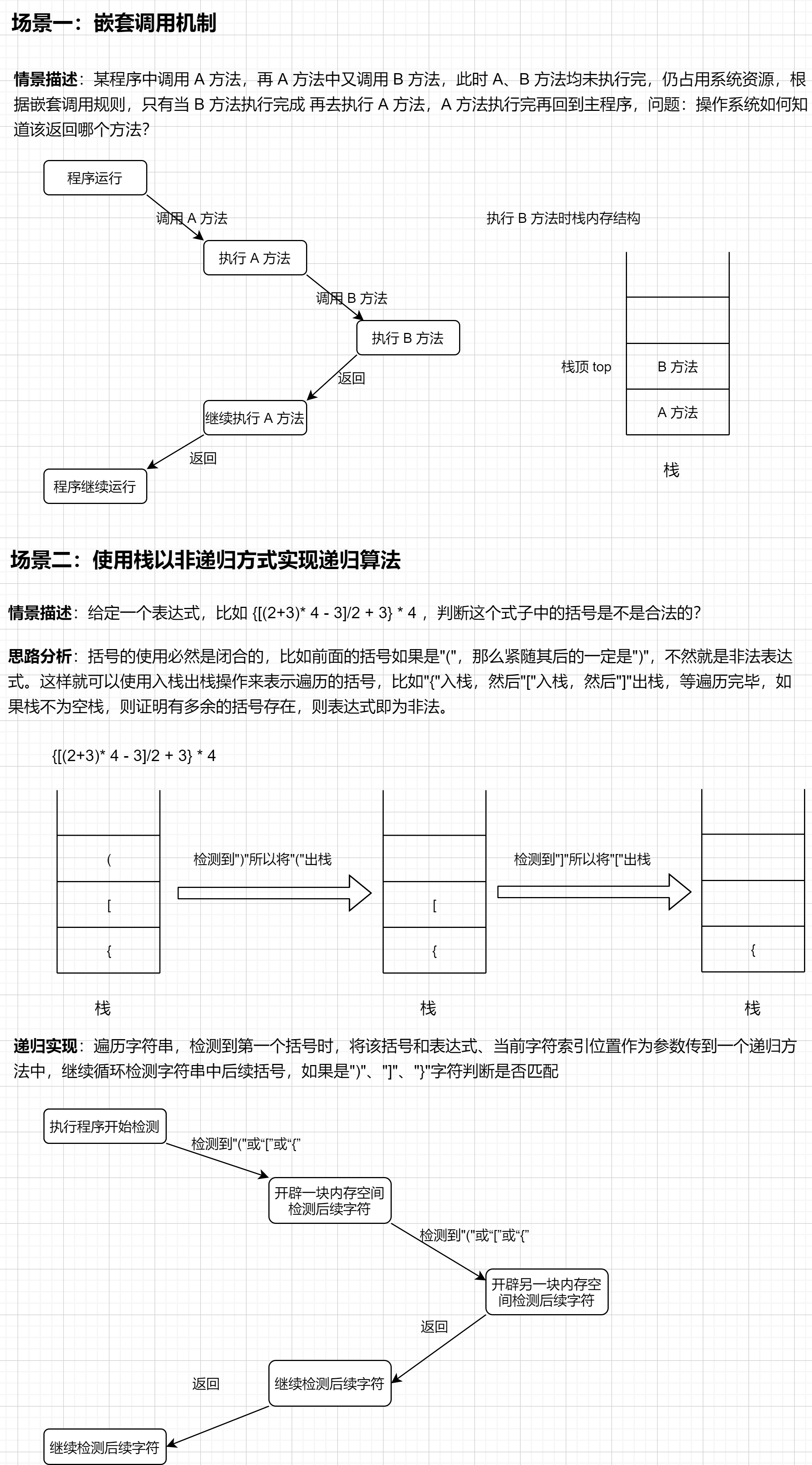
经典场景举例:
-
嵌套调用的实现机制特别适合栈这种结构
-
判断表达式"{[(1+3)7+(3+4)2]/2-1}3"、"{[(1+3)7+(3+4)2]/2-1)}3"中括号是否合法?
这里判断是否合法的标准:不做"()" "{}" "[]"之间的优先级判断,每一个括号都是成对出现,且每对括号之间都是自然数对括号,出现奇数个括号即为非法。
使用栈数据结构实现:
/** * 判断给定表达式中的括号是否合法 * <p> * 所判断括号的种类范围:() [] {} * </p> * * @param expression * @return */ public boolean judgeBracketInExpressionIsValid(String expression) { SeqStack<String> stringLinkedStack = new SeqStack<>(expression.length()); HashMap<String, String> hashMap = new HashMap<String, String>() { { put(")", "("); put("]", "["); put("}", "{"); } }; for (int i = 0; i < expression.length(); i++) { char ch = expression.charAt(i); switch (ch) { case '(': case '[': case '{': // 入栈 stringLinkedStack.push(ch + ""); break; case ')': case ']': case '}': // 出栈 if (stringLinkedStack.isEmpty() || (!stringLinkedStack.pop().equals(hashMap.get(ch + "")))) { return false; } break; default: break; } } // 如果能执行到这里,判断栈中是否还有剩余元素,如果有剩余元素则证明表达式中括号不合法 return stringLinkedStack.isEmpty(); }使用递归思想实现:
/** * 递归方式实现判断表达式中括号是否非法 * * @param expression * 给定表达式 * @return boolean */ public boolean judgeBracketInExpressionIsValidRecursion(String expression) { // 为取数据做准备 Map<String, String> afterBracketMap = new HashMap<String, String>(3) { { put(")", "("); put("]", "["); put("}", "{"); } }; Map<String, String> frontBracketMap = new HashMap<String, String>(3) { { put("(", "placeholder"); put("[", "placeholder"); put("{", "placeholder"); } }; // 调用递归方法 int handleResult = judgeBracket(expression, -1, afterBracketMap, frontBracketMap, null); return handleResult < 0 ? false : true; } /** * 递归检测字符 * <p> * 其中检测字符的索引游标需要注意下 * </p> * * @param expression 待检测表达式 * @param index 检测过的表达式中字符索引游标值 * @param afterBracketMap 后括号数据映射集合 * @param frontBracketMap 前括号数据映射集合 * @param targetBracket 待比较字符 * @return int 返回值 > 0 合法;返回值 < 0 不合法。 */ public int judgeBracket(String expression, int index, Map<String, String> afterBracketMap, Map<String, String> frontBracketMap, String targetBracket) { for (int i = index + 1; i < expression.length(); i++) { char charAt = expression.charAt(i); if (frontBracketMap.get(charAt + "") != null) { // 出现了新的前括号,直接开辟新的内存空间检测 int handle = judgeBracket(expression, i, afterBracketMap, frontBracketMap, charAt + ""); if (handle < 0) { return handle; } // 检测完毕将已检查到的位置的游标返回 i = handle; } else if (afterBracketMap.get(charAt + "") != null) { // 如果后括号出现,那么前面比较符号如果不对应或者为null均为不合法 return afterBracketMap.get(charAt + "").equals(targetBracket) ? i : -1; } } return 1; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号