算法心得（4）**快速排序和归并排序**

我们这里讨论的排序是把数组元素排成从小到大的顺序（升序）

**快速排序**

先直接上模板：

/****************
 * function:对数组进行快速排序
 * para:q[](待排序数组)，l(数组左边界)，r(数组右边界)
 * return:void
 */
void fastSort(long long q[], int l, int r)
{
    if (l >= r)
        return;
    int mid = q[l + r >> 1];    // 选取参照值，可以随便挑一个选
    int i = l - 1, j = r + 1; // 边界值，为了后面的++和--能操作
    while (i < j)
    {
        do
            i++;
        while (q[i] < mid); // 扫描。用于找到需要相互交换的元素
        do
            j--;
        while (q[j] > mid);
        if (i < j) 
        // 虽然上一层while里面有了，但是这个条件是为了防止循环最后出现i=j或者i>j的情况，这两个条件都是不需要交换的
        {
            int temp = q[i];
            q[i] = q[j];
            q[j] = temp;
        }
    }
    fastSort(q, l, i - 1); // 最后一次递归的时候，i=j，所以这里是i-1
    fastSort(q, j + 1, r);
}

 **快排思路**

快排的主要思路是设定参照值，凡是大于它的元素，都放在它的右边，凡是小于它的，都放在左边

 

举例来说，对于一个数组A：

 

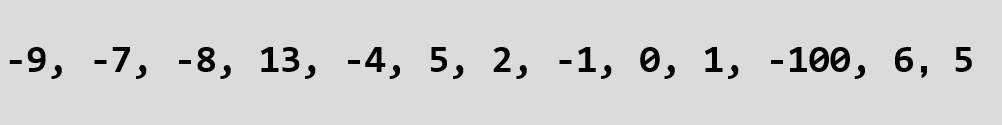
我们把设置两个指针，分别指向它的开头和末尾：

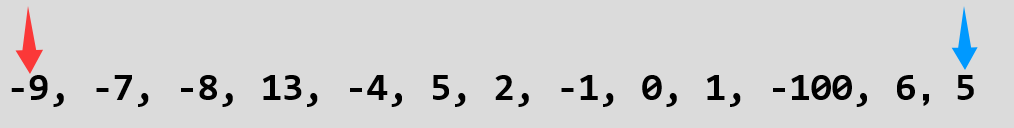
然后从数组中选取某一参照值，从哪里选的都一样，这里选取的是数组中间的值：

 

随后红指针向后扫描，蓝指针向前扫描，当红指针指向的数字大于等于参照值时红指针停下，当蓝指针指向的数字小于等于参照值时蓝指针停下：

 

将两者交换顺序：

之后继续扫描：

交换：

继续扫描：

交换：

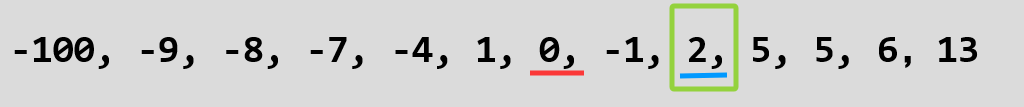
继续扫描，当红蓝指针相遇时，排序结束：

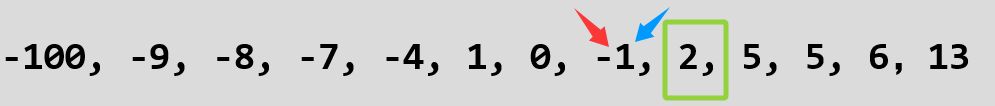
此时我们不难发现，参照值2的左边都是小于它的，右边都是大于它的

随后进入递归，分别处理交换了两个指针扫描过了的区域：

 

递归的出口是数组只有一个元素时

 

 **快排的复杂度**

快排的理想情况是，红蓝指针相遇在数组的正中间，考虑到扫描和比较的时间，此时的时间复杂度公式为：T[n] = 2T[n/2] + f(n)；      时间复杂度：   O(n) = O( nlogn )

最坏的情况是：每一次取到的参照值都是数组中最小/最大的，这样相当于冒泡排序，因为每一次完整的扫描只调整了一个元素的位置（调整了参照值的位置）此时的时间复杂度   O(n) = O( n^2 )

 

**归并排序**

也是直接上模板：

 

/****************
 * function:对数组进行归并排序
 * para:q[](待排序数组)，l(数组左边界)，r(数组右边界)
 * return:void
 */
long long p[N]; // 辅助数组
void mergeSort(long long q[], int l, int r)
{
    if (l >= r)
        return;
    int pos_mid = l + r >> 1;
    mergeSort(q, l, pos_mid); // 先递归再处理
    mergeSort(q, pos_mid + 1, r);
    int i1 = 0;
    int i = l, j = pos_mid + 1;
    while (i <= pos_mid && j <= r)
    {
        if (q[i] <= q[j])
        {
            p[i1++] = q[i++];
        } // p是全局数组
        else
            p[i1++] = q[j++];
    }
    while (i <= pos_mid)
        p[i1++] = q[i++];
    while (j <= r)
        p[i1++] = q[j++];                // 扫描，把比较时没有放进p数组的元素放进去
    for (i = l, j = 0; i <= r; i++, j++) // 再把p中排好的元素重新放回原数组中
        q[i] = p[j];
}

 **归并排序思路**

归并排序算法的基本思路是将两个有序数组合并成一个更大的有序数组。它分为两部分：一个是分，也就是把原数组划分成两个子数组的过程。另一个是治，它将两个有序数组合并成一个更大的有序数组。

它是先递归再排序。关键步骤在于使用一个辅助数组来暂存元素

首先将序列拆分成两个两个元素一组（也有可能奇数时，有的组只有一个元素），然后排序，排序后把小组组合起来，变成四个四个一组（也有可能是2+1=3个一组），再排序。思路比较简单，重点在于对它与快排的比较。

**归并排序复杂度**

归并排序对于每一种情况，都要递归、把元素复制到辅助数组、再把辅助数组的元素放回原数组，所以对每一种情况的复杂度都是一样的。

其时间复杂度公式为：T[n] = 2T[n/2] + f(n)；      时间复杂度：   T(n) = O( nlogn )

空间复杂度因辅助数组的存在： S(n)=O(n)

**两种排序的比较**

**递归顺序**

快排和归并每一次排序，虽然对于整个数组而言，得到的结果并不一定是最终结果，但是都让数组往“有序”的方向演变。

快排是先排序再递归，归并排序是先递归再排序，前者是自顶向下（在拆分的过程中排序），后者是自底向上（拆分到最小单元后排序）。

**稳定性**

归并排序是一种稳定的排序算法。稳定性在排序算法中指的是能够保证排序前两个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。

而快速排序不稳定，比如对于，在第一次扫描中，红框的5与红框的2交换，蓝框的5与蓝框的2交换：

原本相对位置上，红框的5是在蓝框的5的前面的，红框的2是在蓝框的2的后面的，经过交换后，相等的元素彼此之间的相对位置都颠倒了。所以快排是不稳定的。

**思路的区别**

快排设置参照值（哨兵值），它因为参照值的存在而具有最坏的情况（每次选取的参照值为最小最大时）；而归并排序使用辅助数组，以空间换时间，使得每一种情况的复杂度都是一样的。