算法心得（2）**前缀和**

**思路**

前缀和的思想就是  **把影响累加起来，每一次累加都作一次记录**

一般在情况满足两个条件时就使用它： （1）影响可以累加   （2）有多个查询

就拿计算二维矩阵面积来说:

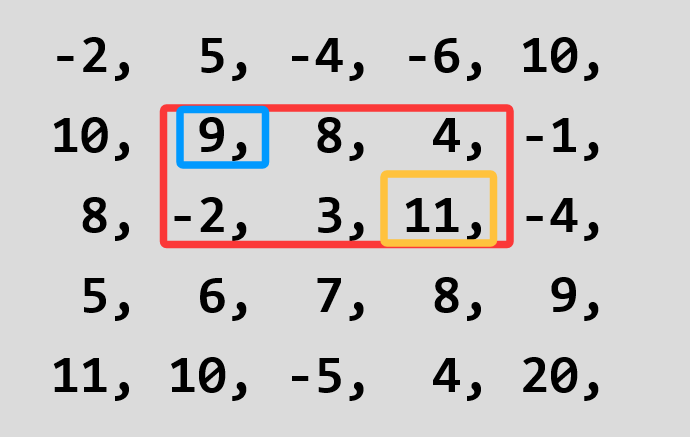
图中红框框起的一个子矩阵的面积为9+8+4-2+3+11=33，同时以左上角（蓝框，坐标为（2，2））和右下角（黄框，坐标为（3，4））定位这个子矩阵，我们说（2，2）到（3，4）的子矩阵的面积为33。

那么问题来了，如果要我们要反复查询（x1，y1）到（x2，y2）的子矩阵面积，其中x1，y1，x2，y2是不断变化的，那我们是不是要每一次查询都要把子矩阵的内容一个一个加起来算面积？这样未免也太繁琐了。

因为每一次的计算，会对一些元素进行反复的计算，如：

计算红框和蓝框两个子矩阵的面积，会发现3+11被计算了两次，这个重叠部分可以优化，于是便有了前缀和。

我们首先计算每一个以（1，1）为左上角的子矩阵的面积：

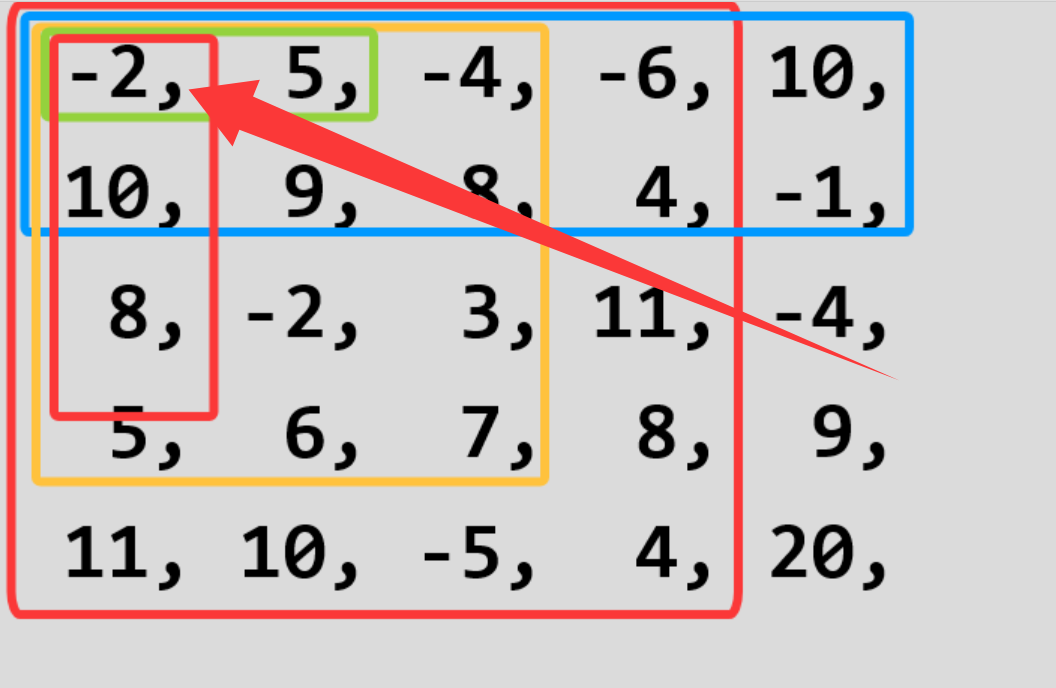
把计算结果保存在一个与原矩阵同样大小的矩阵，该矩阵成为前缀和矩阵：

保存原则是这样的：左上角坐标为（0，0），右下角坐标为（i，j）的子矩阵的面积保存在（i，j）的位置，比如原矩阵中（0，0）到（4，3）的子矩阵的面积为53，保存到上图的（4，3）的位置。

那么最主要的问题就是，怎么查询一个左上角坐标不为（0，0）的子矩阵的面积？

比如要查这个：    那我们可以进行一些变换：

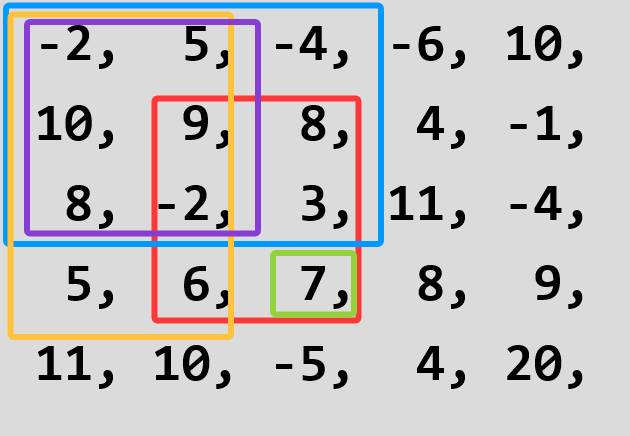
红框的面积就是蓝框+黄框+绿框-紫框，由于蓝框、黄框、紫框的面积已经保存在了前缀和矩阵中，而绿框面积又不用计算，所以对于红框的子矩阵：（2，2）到（4，3）的面积=前缀和[4，2]+前缀和[3，3]+7-前缀和[3，2]。

给出相对普适一点的代码模板：

#include <stdio.h>
const int N = 100010;
int a[N][N]; // 原矩阵
int S[N][N]; // 前缀和矩阵
int main()
{
    int n; // 矩阵行数
    int m; // 矩阵列数
    int i, j;
    for (i = 1; i < n; i++) // 注意，下标是从1开始的，这是为了利用为0的S[0][n]和S[n][0]
        for (j = 1; j < m; j++)
        {
            scanf("%d", a[i][j]);
            S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j]; // 求前缀和
        }
    for (i = 1; i < n; i++)
    {
        for (j = 1; j < m; j++)
            printf("%d, ", S[i][j]);
        printf("\n");
    }
    return 0;
}

由此可以看出，前缀和的思想就是把影响累加，然后通过不同的累加之间的运算，减少每次查询之间重叠的开销。

**例题**

第31次CSP认证考试中的第二题，“坐标变换（其二）”：

经过思考，每一次对坐标的操作是可以累加的，并且有多次查询，所以适合使用前缀和，把每次拉伸的k倍和旋转的<span id="MathJax-Span-160" class="mrow"><span id="MathJax-Span-161" class="mi">θ分别用一维数组记录累加的前缀和即可。