数制和码制

几种常用的数制

十进制

  任意一个多位的十进制数 \(D\) 均可展开为 \(D=\sum{k_i}10^i\)。若以 N 取代上式中的 10，即可得到多位任意进制（N进制）数展开式的普遍性形式

\[D=\sum{k_i}N^i \]

式中 \(N\) 称为计数的基数，\(k_i\) 为第 \(i\) 位的系数， \(N^i\) 称为第 \(i\) 位的权。

二进制

  目前在数字电路中应用最广泛的是二进制。任何一个二进制数均可展开为 \(D=\sum k_i2^i\) 并可用上式计算出它所表达的十进制数的大小。例如

\[(101.11)_2=1\times 2^2+0\times 2^1+1\times 2^{-1}+1\times 2^{-2}=(5.75)_{10} \]

  上式中分别使用下脚注 2 和 10 表示括号里的数是二进制数和十进制数。有时也用 B(Binary) 和 D(Decimal) 代替 2 和 10 这两个脚注。

八进制

  任意一个八进制数可展开为 \(D=\sum k_i8^i\) 。并可利用上式计算出与之等效的十进制数值。例如

\[(12.4)_8=1\times 8^1+2\times 8^0+4\times 8^{-1}=(10.5)_{10} \]

  有时也可用 O(Octal) 代替下脚注 8，表示 8 进制数。

十六进制

  十六进制数每一位分别用 0~9、A(10)、B(11)、C(12)、D(13)、E(14)、F(15) 表示。因此，任意一个十六进制数均可展开为 \(D=\sum k_i16^i\) 并可由此式计算出它所表示的十进制数值。例如

\[(2A.7F)_{16}=2\times 16^1+10\times 16^0+7\times 16^{-1}+15\times 16^{-2}=(42.4960937)_{10} \]

式中的下脚注 16 表示括号里的数是十六进制数，有时也可用 H(Hexadecimal) 代替这个脚注。

不同数制间的转换

二 - 十转换

  将二进制数转换为等值的十进制数称为二-十转换。转换时只要将二进制数展开，然后将所有各项的数值按十进制数相加，就可以得到等值的十进制数了。例如

\[(1011.01)_2=1\times 2^3+0\times 2^2+1\times 2^1+1\times 2^0+0\times 2^{-1}+1\times 2^{-2}=(11.25)_{10} \]

十 - 二转换

  所谓十-二转换，就是将十进制数使用短除法转换为等值的二进制数。

• 首先讨论整数的转换。例如，将 \((173)_{10}\) 转换为二进制数可如下进行
  
  最后将余数倒着从下往上写便是其二进制数，故 \((173)_{10}=(10101101)_2\) 。
• 其次讨论小数的转换。例如，将 \((0.8125)_{10}\) 化为二进制小数时可如下进行
  
  最后将整数部分从上往下写便是其二进制数，故 \((0.8125)_{10}=(0.1101)_2\) 。

二进制算术运算

二进制算术运算的特点

  当两个二进制数码表示两个数量大小时，他们之间可以进行数值运算，这种运算称为算术运算。例如，两个二进制数 1001 和 0101 的算术运算有


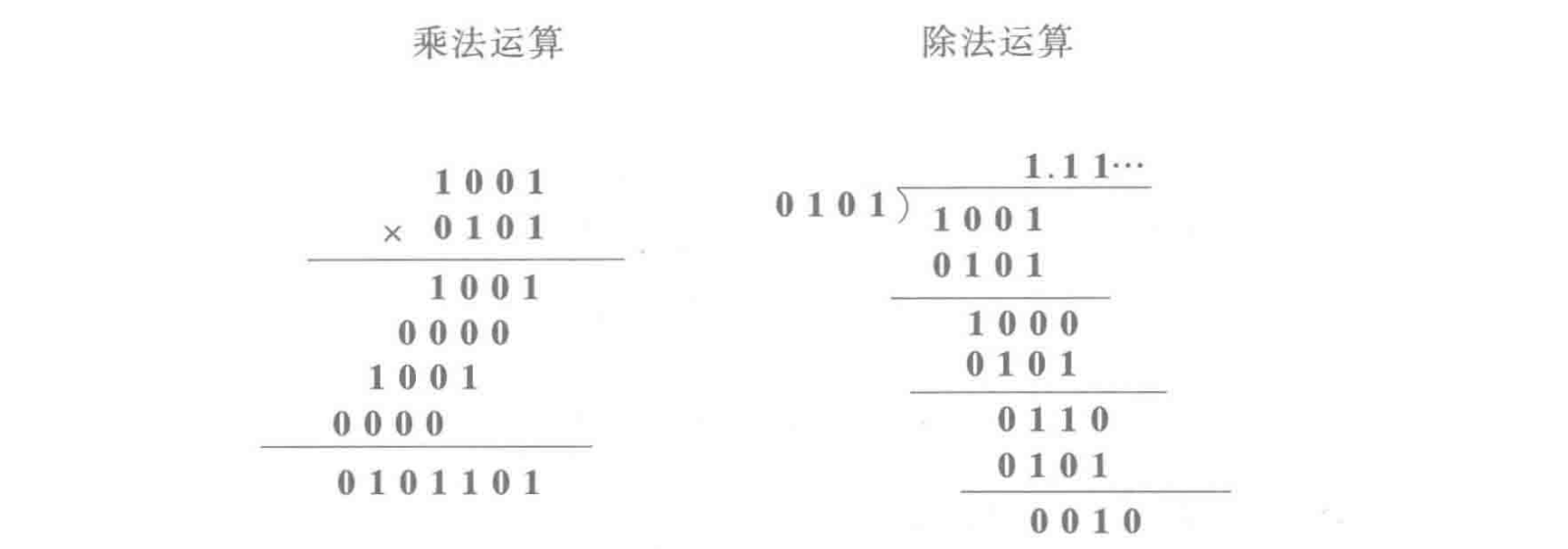
  从上面两个例子可以看到二进制算术运算的两个特点，即二进制数的乘法运算可以通过若干次的“被乘数（或零）左移一位”和“被乘数（或零）与部分积相加”这两种操作完成；而二进制的除法可以通过若干次的“除数右移一位”和“从被除数或余数中减去除数”这两种操作完成。

反码，补码和补码运算

  在数字电路中，使用逻辑电路输出的高低电平表示二进制数的 1 和 0 ，而正负则在二进制数前增加一位符号位来表示。符号位为 0 则表示这个数是正数，符号位为 1 则表示这个数是负数。这种形式的数称为原码。