查找

定义

• 查找表：用于查找的数据集合称为查找表，查找表一般有4种操作
  • 查询某个特定的值使得否在查找表中
  • 检索满足条件的某个特定的数据元素的各种属性
  • 在查找表中插入一个数据元素
  • 从查找表中删除某个数据元素
• 静态查找表：若一个查找表的操作只涉及查询和检索某个元素的属性，则无须动态修改查找表。如：顺序查找，折半查找
• 动态查找表：需要动态地插入或删除的查找表称为动态查找表。如：二叉排序树，二叉平衡树

！折半查找树和二叉平衡树本质上是二叉排序树
！哈夫曼树是最优二叉树，折半查找树是最优二叉排序树

查找方式

顺序查找

• “哨兵”：哨兵位于数组下标为 0 的起始位置，值等于要查找的值 key，这使得从右往左顺序查找时若未找到 key 值或在哨兵位置找到 key 值，则同样返回 0 表示未查找成功，其作用为防止数组越界和节省空间开销

！若从左至右查找则数组的 0 位置不放任何元素

• 平均查找次数 ASL：
  • 查找成功的 ASL 为 \(\frac{n+1}{2}\)
  • 查找失败：
    • 有序表查找失败为 \(\frac{n}{2}+\frac{n+1}{n}\)
    • 无序表查找失败为 \(n+1\)

折半查找二分查找

• 折半查找仅适用于有序的顺序表
• 折半查找判定树中序遍历后是一个递增的有序序列
• 折半查找树平均查找长度 ASL：
  • 当树中结点有无穷多个时（n 趋于无穷大），平均查找长度近似于 \(log_2(n+1)-1\)
  • 查找成功时，ASL 等于每个查找成功结点的查找次数之和除以总成功结点数
  • 查找失败时，ASL 等于每个查找失败结点的查找次数之和除以总失败结点数

下标	0	1	2	3	4	5	6	7
值	5	13	27	39	45	52	72	81

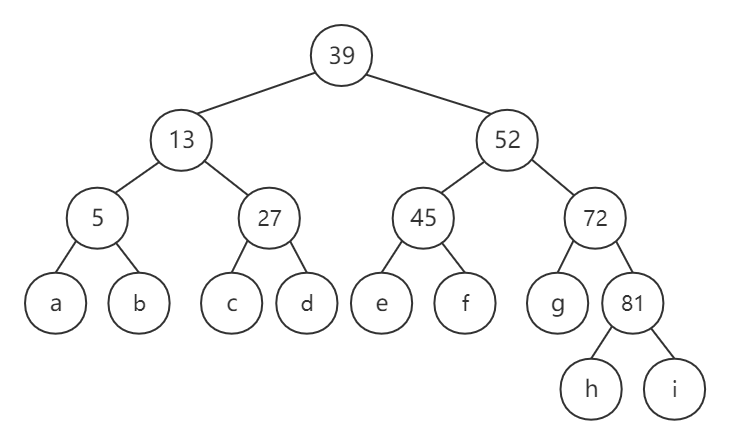
该树查找成功的的 ASL（有数值的结点的ASL）为 \(\frac{3+2+3+1+3+2+3+4}{8}＝\frac{21}{8}\) ，失败的 ASL（字母节点的ASL）为 \(\frac{3+3+3+3+3+3+3+4+4}{9}=\frac{29}{9}\)

• 折半查找时间复杂度为 \(O(log_2n)\)

分块查找

• 分块查找的查找表每一块之间是有序的（总体从小到大），每一块之内是随意的，每一块的关键字为该块最大值元素的值
• 若一长度为 n 的查找表若采用分块查找，则最优的分块个数 b 为 \(\sqrt{n}\)，平均查找长度 ASL 为 \(\sqrt{n}+1\)
• 若该每块有 s 个记录，在等概率情况下：
  • 若块间采用折半查找，块内为顺序查找，则 \(ASL_{分块}=ASL_{折半}+ASL_{顺序}=\lceil log_2(b+1)\rceil+\frac{1+s}{2}\)
  • 若块间和块内均采用顺序查找，则 \(ASL_{分块}=ASL_{块间顺序}+ASL_{块内顺序}=\frac{1+b}{2}+\frac{1+s}{2}\)
• 分块查找查找的时间复杂度为 \(O(\sqrt{n})\)

二叉排序树

• 同折半查找树一样其中序序列为从小到大顺序排列
• 其目的是提高查找与插入、删除关键字的速度，而不是为了排序
• 二叉排序树的性能与其形状有关，最好情况下（平衡二叉树）其查找时间复杂度为 \(O(log_2n)\)；最坏情况下（只有左或右子树的树）为 \(O(n)\)，平均查找长度 ASL 为 \(O(log_2n)\)，其修改，插入删除的时间复杂度也为 \(O(log_2n)\)

二叉排序树的插入

E.G.

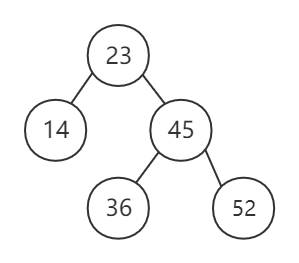
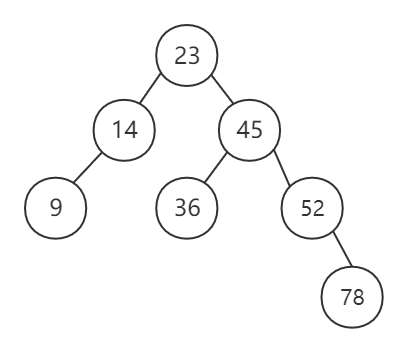
按照序列 (23, 45, 14, 52, 36, 78, 9) 建立一棵二叉排序树

解：

• 若树为空则直接插入

• 比较待插入的值与已插入所有结点值大小，若为较小值，则插入左子树，若为较大值，则插入右子树

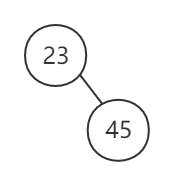
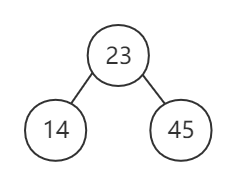
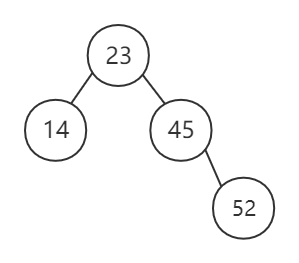
二叉排序树的删除

• 若删除结点为叶结点，则直接删除
• 若删除的结点仅有左孩子或右孩子，则用左/右孩子代替该结点
• 若删除的结点均有左右孩子，则找到待删除结点的直接前驱或直接后继结点，用该结点来替换待删除结点后再删除该结点

！使用中序遍历来寻找直接前驱和直接后继
！删除有左右孩子结点的二叉树排序树，其结果不唯一

平衡二叉树

• 平衡二叉树任意结点的左、右子树高度差绝对值不超过 1
• 平衡因子：某一结点的左子树与右子树的高度差（左子树高度减右子树高度），其值只可能为 -1, 0, 1
• 查找的效率与二叉树的深度有关

平衡二叉树的插入

• LL 平衡旋转：由于在结点 n 的左孩子的左子树上插入了结点
  • 将结点 n 向下旋转，使其成为它左孩子结点的右结点，调整子树使其为二叉排序树
• RR 平衡旋转：由于在结点 n 的右孩子的右子树上插入了结点
  • 将结点 n 向下旋转，使其成为它右孩子结点的左结点，调整子树使其为二叉排序树
• LR 平衡旋转：由于在结点 n 的左孩子的右子树上插入了结点
  • 将待插入的结点的父结点替换掉结点 n，调整子树使其为二叉排序树
• RL 平衡旋转：由于在结点 n 的左右孩子的左子树上插入了结点
  • 将待插入的结点的父结点替换掉结点 n，调整子树使其为二叉排序树

E.G.

按照序列 (34, 23, 15, 98, 115, 28, 107) 建立一棵平衡二叉树

解：

• 插入结点 34, 23, 15

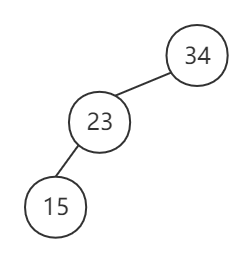
• 由于插入结点 15 使平衡因子为 2，则需将其平衡。该调整为 LL 平衡旋转，最近的平衡因子绝对值大于 1 的结点为 34，则将结点 34 向下旋转为结点 23 的右孩子，插入结点 98, 115

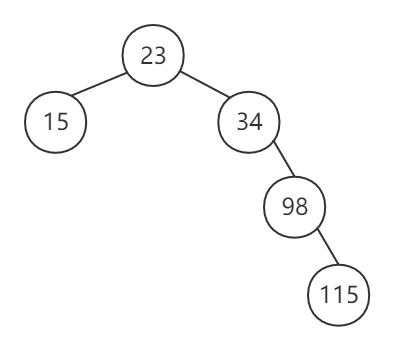
• 由于插入结点 115，使平衡因子为 -2，则需将其平衡。该调整为 RR 平衡旋转，最近的平衡因子绝对值大于 1 的结点为 34，则将其向下旋转为结点 98 的左孩子，调整为二叉排序树，再插入结点 28

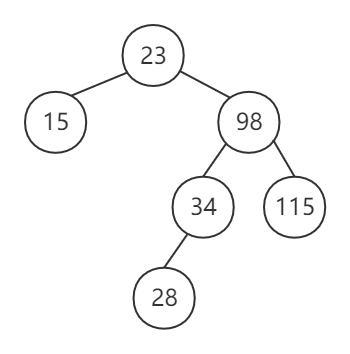
• 由于插入结点 28，使平衡因子为 -2，则需将其平衡。该调整为 RL 平衡旋转，最近的平衡因子绝对值大于 1 的结点为 23，则将待插入结点 28 的父结点，即结点 34 顶替至结点 23 的位置，将结点 23，结点 15，结点 28 与 107 插入合适的位置

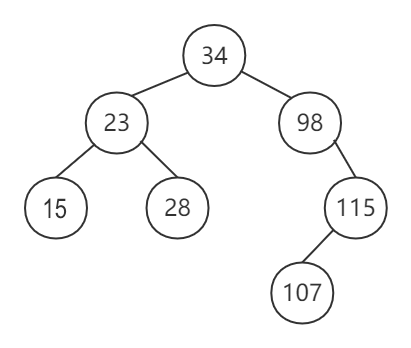
• 由于插入结点 107，使平衡因子为 -2，则需将其平衡。该调整为 RL 平衡旋转，最近的平衡因子绝对值大于 1 的结点为 98，则将待插入结点的父结点，即结点 115 顶替至结点 98 的位置，将结点 98 与 115插入合适的位置

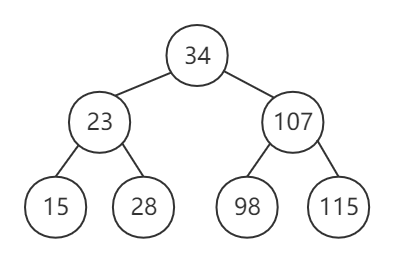
B树

• 一棵 m 阶B树，树中每个结点至多有 m 棵子树，即至多含有 m-1 个关键字
• 除根结点外的所有非叶结点至少有 \(\lceil \frac{m}{2} \rceil\) 棵子树，即至少含有\(\lceil \frac{m}{2} \rceil-1\) 个关键字
• 所有的叶结点都出现在同一层次上
• 不支持顺序检索

B树的插入

• 若结点不满，则插入相应位置
• 若结点已满，则按顺序将中间的关键字提升进父结点，剩余结点中的俩数分裂为两个结点

E.G.

有如下一棵B树，插入 26, 7

解：
                

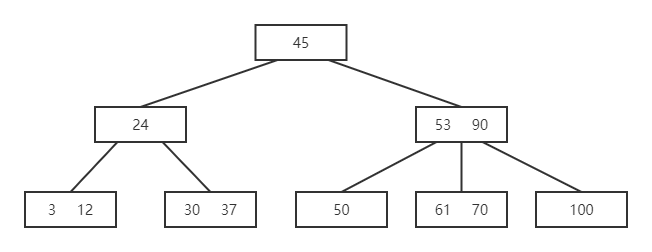
• 插入 26

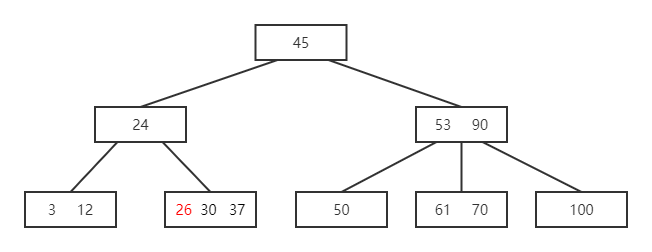
• 因该 B 树为 3 阶，则每个结点最多为 2 个关键字，需将该结点中间的关键字提升，并将该结点分裂

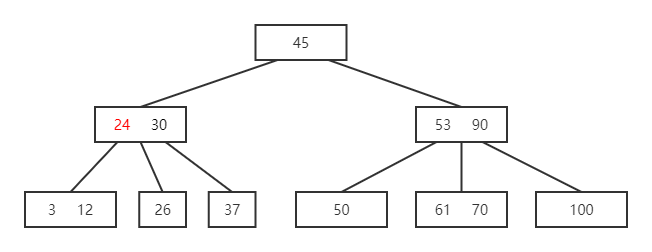
• 再插入 7

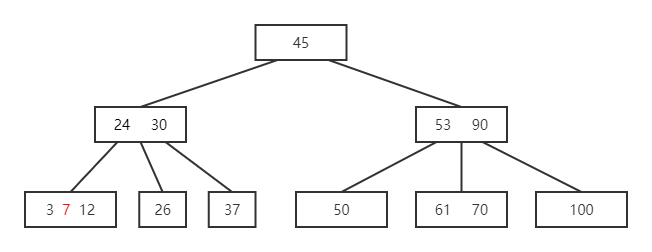
• 同理提升 7，并将该结点分裂

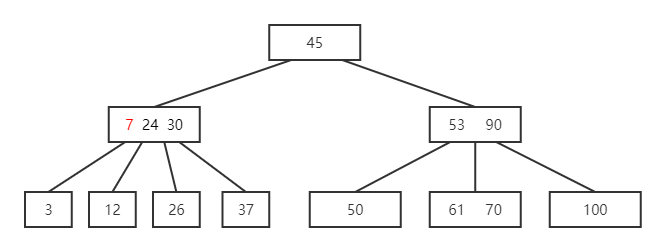
• 由于父结点关键字也超出，将 24 提升并分裂

B树的删除

• 若删除的关键字在终端节点上
  • 若结点内关键字数量大于 \(\lceil \frac{m}{2}\rceil -1\) ，则直接删除
  • 若结点内关键字数量等于\(\lceil \frac{m}{2}\rceil -1\) ，且其左右兄弟结点中存在关键字数量大于\(\lceil \frac{m}{2}\rceil -1\) 的结点，则向其父结点中的直接前驱 (后继) 借关键字，该父结点中的直接前驱 (后继) 再向其直接前驱 (后继) 借关键字
  • 若结点内关键字数量等于\(\lceil \frac{m}{2}\rceil -1\) ，且其左右兄弟结点中不存在关键字数量大于\(\lceil \frac{m}{2}\rceil -1\) 的结点，则需要进行结点合并
• 若删除的关键字不在终端节点上
  • 存在关键字数量大于\(\lceil \frac{m}{2}\rceil -1\) 的左子树或右子树，则用待替换掉关键字的前驱或后继替换待删除的关键字
  • 左右子树的关键字数量均等于\(\lceil \frac{m}{2}\rceil -1\) ，则将这两个左右子树合并，然后删除待删除的关键字
• B 树的删除图解

E.G. 1 在终端结点上

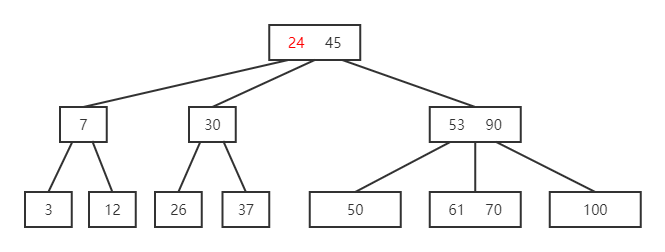
如果所示一棵 B 树，删除关键字 50 后再删除53

解：
                

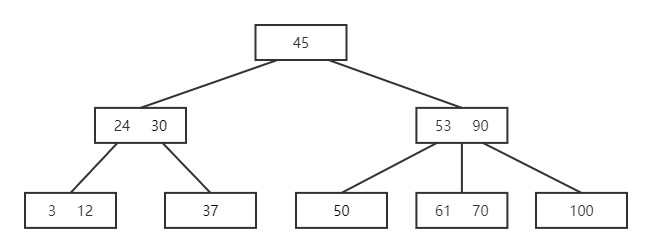
• 删除 50，需借其直接后继53，53 需借其直接后继 61

                

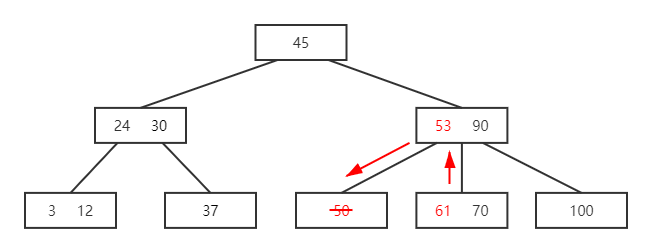
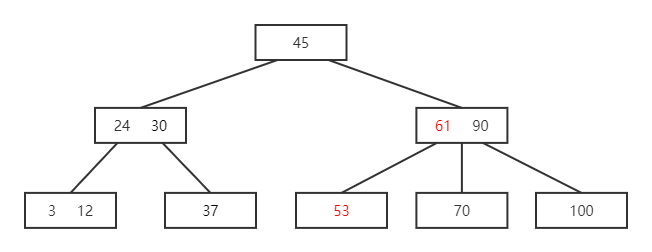
• 再删除 53

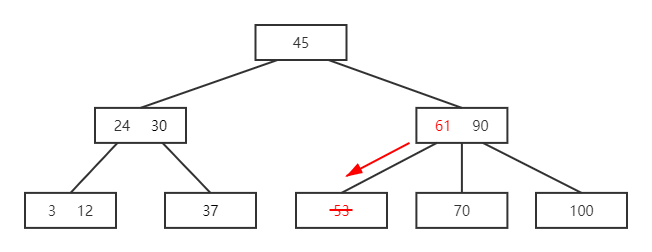
• 61 无后继可借，则将 61 与 70 合并

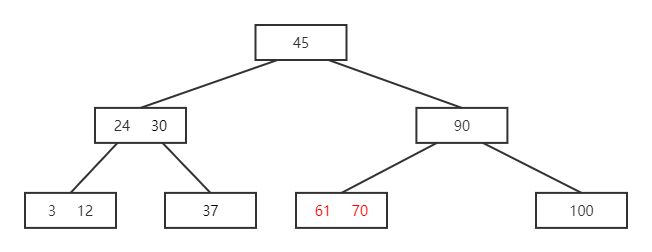
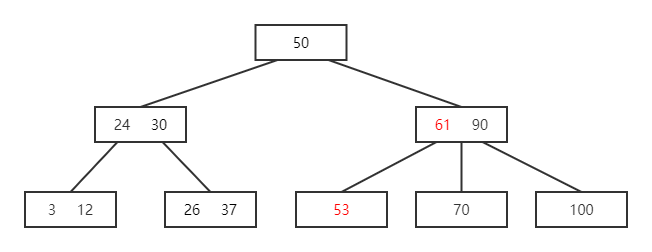
如图所示一棵 B 树，删除 37

解：
                

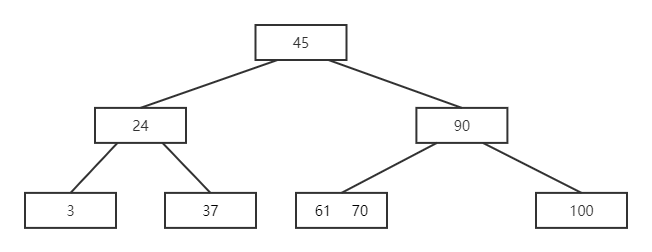
• 删除 37，则向 24 借，24 向 3 借，但 3 无后继可借，则将 3 与24合并

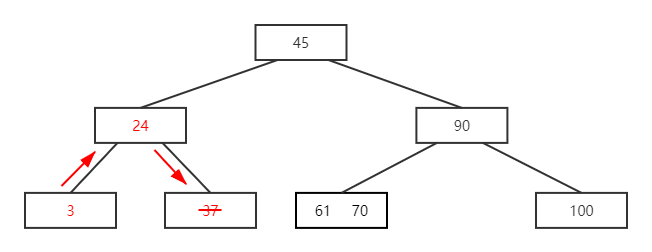
• 合并后其父结点为空，则向后继 45 借，45 向后继 90 借，90 和 该空结点同级不可向下借，则合并45 和 90

  

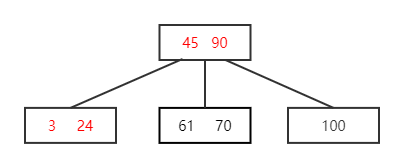
E.G. 2 不在终端结点上

如图所示删除结点 45

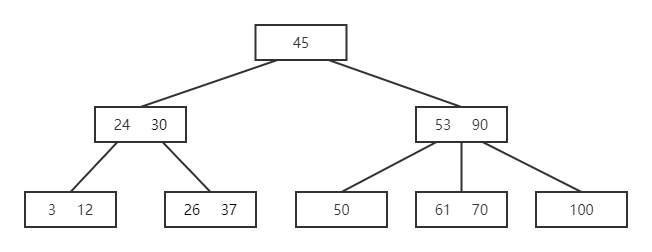
• 结点 45 找到直接后继 50，结点 45 直接借 50

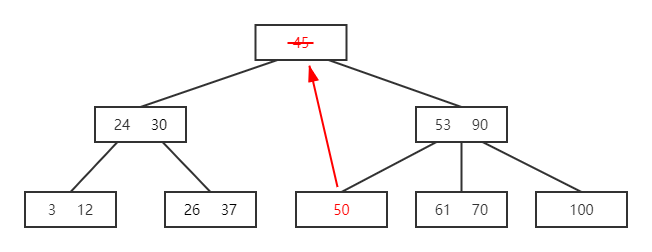
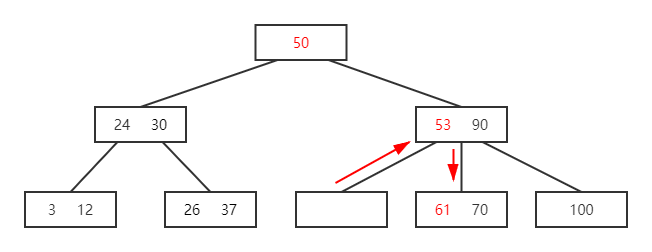
• 结点 50 不可为空借后继关键字 53，结点关键字 53 借直接后继关键字 61

散列表

• 散列函数可能会把两个或两个以上的不同关键字映射到同一地址，称这种情况为冲突，这些发生碰撞的不同关键字称为同义词
• 散列表建立了关键字和存储地址之间的一种直接映射关系

散列函数的构造方法

• 直接定址法：直接取关键字的线性函数值为散列地址，函数为 \(H(key)=key\) 或 \(H(key)=a\times key+b\)
  • 优缺点：
    • 优点：不会产生冲突
    • 缺点：产生的空位较多，会造成存储空间的浪费
• 除留余数法：设表长为 m，取一个不大于 m 但最接近于 m 的质数 p，利用 \(H(key)=key\ \%\ p\) 将其构造

处理冲突的方法

• 装填因子：装填因子表示一个表的的装满程度，其决定了散列表的查找性能，装填因子 \(α=\frac{表中记录数\ n}{散列表长度\ m}\)，若已知装填因子与关键字个数求散列表长度，则 n 除以 α 后若不为整数应当向上取整

线性探测法

• 冲突发生时，顺序查看表中下一个单元直到找出一个空闲单元或查遍全表
• 平均查找长度 ASL：
  • 查找成功时为每个记录的查找长度除以总记录数
  • 查找失败时为散列表范围内每个记录查找失败的长度（包含空记录）除以取余的质数 p

E.G.

现有长度为15且初始为空的散列表，散列函数是 \(H(key)=key\ \%\ 13\) ，按线性探测法处理冲突，将关键字序列 {19, 14, 23, 01, 68, 20, 84, 27, 55, 11, 10, 79} 依次插入散列表，并求其查找成功和失败的 ASL

解：

• 先按除留余数法构造表

列下标	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
值		14		68			19	20			23	11

• 01 余 13 剩 1，但 1 位置有 14，则找到下一个空位填入，即为 2，27 余 13 为 1，找到下一个空位 4

列下标	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
值		14	01	68	27	55	19	20	84	79	23	11	10

• 查找成功 ASL，14 直接查找，次数为 1，01 先查 1 号位，为 14，则向下一位查找，即其查找次数为 2，68 直接查找，27 直接查找为 1 号位，则向后依次查找，即其查找次数为 4

列下标	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
值		14	01	68	27	55	19	20	84	79	23	11	10
查找数		1	2	1	4	3	1	1	3	9	1	1	3

• 查找成功 ASL 为 \(\frac{1\times6+2+3\times3+4+9}{12}=2.5\)
• 处理查找失败的 ASL，先定位散列表范围，范围为 p - 1 即 0~12，再写出每个项失败次数，失败次数即为向右查找直到找到空为止的次数，若自身为空则为 1，该题范围为 0~12，则在 12 后构造一个不计入计算的空项来辅助填写查找失败数

列下标	0	1	2	3	4	5	6	7	8	9	10	11	12	13
值		14	01	68	27	55	19	20	84	79	23	11	10
失败数	1	13	12	11	10	9	8	7	6	5	4	3	2

• 查找失败的 ASL 为 \(\frac{1+13+12+11+10+9+8+7+6+5+4+3+2}{13}=7\)

拉链法链接法

• 将所有同义词存储在一个线性链表中，这个线性链表由其散列地址唯一标识
• 平均查找长度 ASL：
  • 查找成功时为 \(\frac{1\times第一列元素个数+2\times第二列元素个数...}{元素总个数}\)（竖着看）
  • 查找失败时为每行空结点所在位置相加再除以取余的质数 p（横着看）

！其ASL直接与哈希函数有关

E.G.

(题同上) 现有长度为15且初始为空的散列表，散列函数是 \(H(key)=key\ \%\ 13\) ，按链地址法处理冲突，将关键字序列 {19, 14, 23, 01, 68, 20, 84, 27, 55, 11, 10, 79} 依次插入散列表，并求其查找成功和失败的 ASL

解：

• 按拉链法画出该散列表

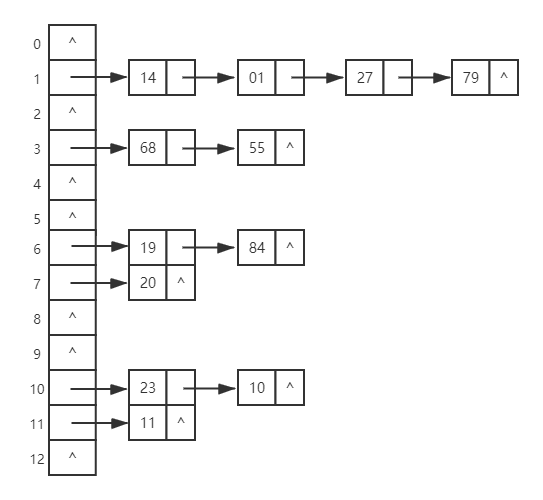
• 该散列表查找成功的平均查找长度为第一列有后继的元素个数乘 1，加第二列有后继元素个数乘 2，加第三列有后继元素个数乘 3 ... 再除以总关键字个数即\(\frac{1\times6+2\times4+3\times1+4\times1}{12}=1.75\)
• 查找失败
  • 不带头结点（默认）：查找失败的平均查找长度为每一行空指针所在列数减 1 之和除以质数，即\(\frac{0+4+0+2+0+0+2+1+0+0+2+1+0}{13}=\frac{12}{13}\)
  • 带头结点：查找失败的平均查找长度为每一行空指针所在列数之和除以质数p，即\(\frac{1+5+1+3+1+1+3+2+1+1+3+2+1}{13}=\frac{25}{13}\)