Chapter 2: Bounding Volume Hierarchies 层次包围盒

　　这部分是目前为止我们正在研究的光线追踪器中最困难和最复杂的部分。我把它放在第二章，这样代码就可以运行得更快，因为它可以重构一些求交测试，当我添加矩形和方框时，我们就不需要再对它们进行重构了。

　　光线 - 物体相交的处理是光线跟踪器中的主要时间瓶颈，时间与需要处理的物体数量成线性关系。 但这是对同一模型的重复搜索，因此我们应该能够以二元搜索的精神进行对数搜索。 因为我们在同一模型上发送数百万到数十亿的光线，我们可以对模型进行分类，然后每个光线交叉点可以是次线性搜索。 两个最常见的排序系列是

　　1)划分空间，

　　2)划分对象。

　　后者通常更容易编码，并且运行速度与大多数模型一样快。

　　//边界体--包围盒

　　对一组图元的边界体的关键思想是找到一个完全包围（边界）所有对象的边界体。 例如，假设您计算了包含10个对象的边界球体。 任何错过边界球体的射线肯定会错过所有十个物体。 如果射线击中了边界球体，那么它可能会击中十个物体中的一个（也可能什么都没击中，考虑到边界体和它所包围的对象必然存在缝隙）。 所以边界代码总是以下形式：

　　if (ray hits bounding object)
　　　　return whether ray hits bounded objects
　　else
　　　　return false

　　关键是我们将对象划分为子集。 我们没有划分屏幕或体。 任何对象只在一个边界体积中，但边界体积可以重叠（因为现实中物体也会有重叠，所以由不同的边界体积划分，自然也会产生重叠现象）。

　　为了使事物具有次线性，我们需要使边界体积分层。 例如，如果我们将一组对象分为两组，红色和蓝色，并使用矩形边界体积，我们将：

　　

　　请注意，蓝色和红色边界体包含在紫色边界体中，但它们可能重叠，并且它们不是有序的 - 它们只是在其内部。 因此，右边显示的树在左右子树中没有排序的概念; 他们只是在里面。 代码是：

　　　　if (hits purple)
　　　　　　hit0 = hits blue enclosed objects
　　　　　　hit1 = hits red enclosed objects
　　　　　　if (hit0 or hit1)
　　　　　　　　return true and info of closer hit
　　　　return false

　　为了实现这一切，我们需要一种方法来执行好的划分，以及将光线-边界体相交的方法。 光线-边界体相交需要快速，并且边界积间距要非常紧凑。 在实践中，对大多数模型来说，与轴心对齐的框比其他的要好，但是如果您遇到不寻常的模型类型时，一定要记住这个设计选择。

　　从现在开始，我们将调用轴对齐的矩形平行六边体（实际上，如果精确的称呼的话，就是这么叫的）轴对齐的边界框或AABB(简称)。任何你想用于光线与AABB相交的方法都是好的。而我们需要知道的是我们是否能够击中它; 我们不需要撞点或法线或我们想要显示的对象所需的任何东西。

　　大多数人使用“平板(slab)”方法。这是基于这样的观察:n维AABB只是n轴对齐区间的交点，通常被称为“平板”。区间就是两个端点之间的点，例如，x使得3 < x < 5，或者更简洁地说是(3,5)中的x。在二维中，两个间隔重叠形成一个二维AABB(矩形):

 　　　　　　

　　为了让光线达到一个间隔，我们首先需要弄清楚光线是否到达边界。例如，在二维中，这是光线参数t0和t1。(如果光线与平面平行，那么它们就没有定义。)

　　　　　　

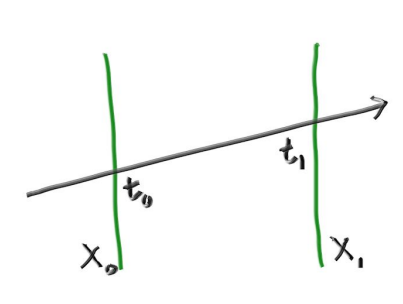
　　在3D中，这些边界是平面。 平面的方程是x = x0，并且x = x1。 光线在哪里击中那个平面？ 回想一下，光线可以被认为是一个给定t返回位置p（t）的函数：

　　　　p (t) = A + t B

　　这个方程适用于x/y/z的三个坐标。例如x(t) = Ax + t*Bx。这条光线在满足这个方程的t点与x = x0平面相交:

　　　　x0 = Ax + t0* Bx

　　因此，在该点处的t为:

　　　　t0 = (x0 - Ax) / Bx

　　我们得到类似的表达式t1 = (x1 - Ax) / Bx。

　　将一维数学转化为命中测试的关键观察是，对于命中，t间隔需要重叠。例如，在2D中，绿色和蓝色的重叠只有在撞击时才会发生:

　　　　　　　　　　

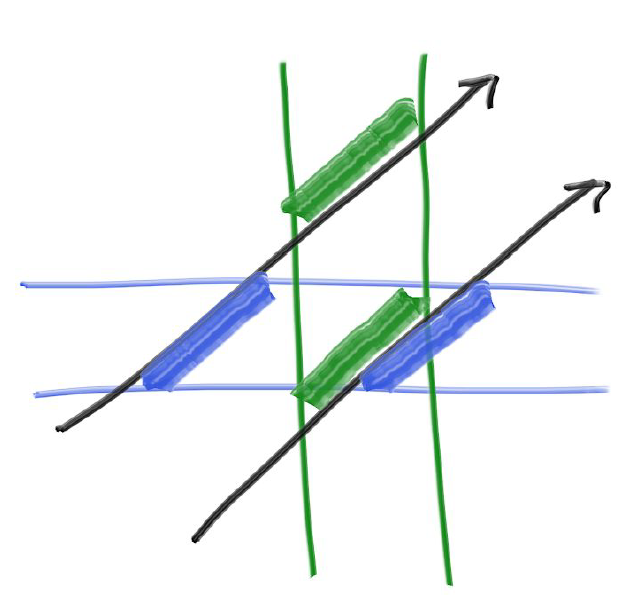
　　什么“板中的t间隔重叠？”在代码中会是这样的：

　　　　compute (tx0, tx1)
　　　　compute (ty0, ty1)
　　　　return overlap?( (tx0, tx1), (ty0, ty1))

　　这是非常简单的，而且3D版本也能工作，这就是为什么人们喜欢平板方法的原因:　　

　　　　compute (tx0, tx1)
　　　　compute (ty0, ty1)
　　　　compute (tz0, tz1)
　　　　return overlap?( (tx0, tx1), (ty0, ty1), (tz0, tz1))

 

　　有一些注意事项使它不如最初看起来那么漂亮。首先，假设射线沿负x方向运动。上面计算的区间(tx0, tx1)可能会被反转，比如(7,3)。如果射线的原点在平板边界上，我们可以得到NaN。在各种光线追踪器的AABB中，有很多方法可以处理这些问题。(还有向量化问题，如SIMD，我们在这里不讨论。如果你想要在矢量化中获得额外的速度，Ingo Wald的论文是一个很好的起点。就我们的目的而言，这不大可能是一个主要的瓶颈，只要我们能使它合理地快速，所以让我们以最简单的方式，这通常是最快的!首先让我们来看看计算间隔:

　　　　tx0 = (x0 - Ax) / Bx
　　　　tx1 = (x1 - Ax) / Bx

　　麻烦的是，完全有效的光线的Bx=0，会导致除法为0。有些光线在平板内部，有些则不是。此外，零将在IEEE浮点下有一个+/-符号。对于Bx=0来说，好消息是tx0和tx1都是+infty，如果不在x0和x1之间，则两者都是-infty。所以，使用最小值和最大值应该能让我们得到正确的答案:

　　　　tx0 = min( (x0 - Ax) / Bx, (x1 - Ax) / Bx);
　　　　tx1 = max( (x0 - Ax) / Bx, (x1 - Ax) / Bx);

　　如果我们这样做，剩下的麻烦的情况是如果Bx = 0并且x0-Ax = 0或x1-Ax = 0，那么我们得到NaN。 在这种情况下，我们可以接受命中或没有命中的结果，但我们稍后会重新审视。

　　现在，我们来看看这个重叠函数。假设我们可以假设区间没有反转(因此第一个值小于区间中的第二个值)，我们希望在这种情况下返回true。同样计算区间(d, d)和(e, e)重叠区间(f, f)的布尔重叠值为:　

　　　　bool overlap(d, D, e, E, f, F)
　　　　　　f = max(d, e)
　　　　　　F = min(D, E)
　　　　　　return (f < F)

　　如果有任何一个NaN在那里运行，比较将返回false，因此我们需要确保我们的边界框中有一个小的填充，如果我们关心放牧情况(我们可能应该这样做，因为在射线跟踪器中所有的情况最终都会出现)。在一个循环中，三个维度同时在间隔tmin内传递，我们得到:、

　　　　

 

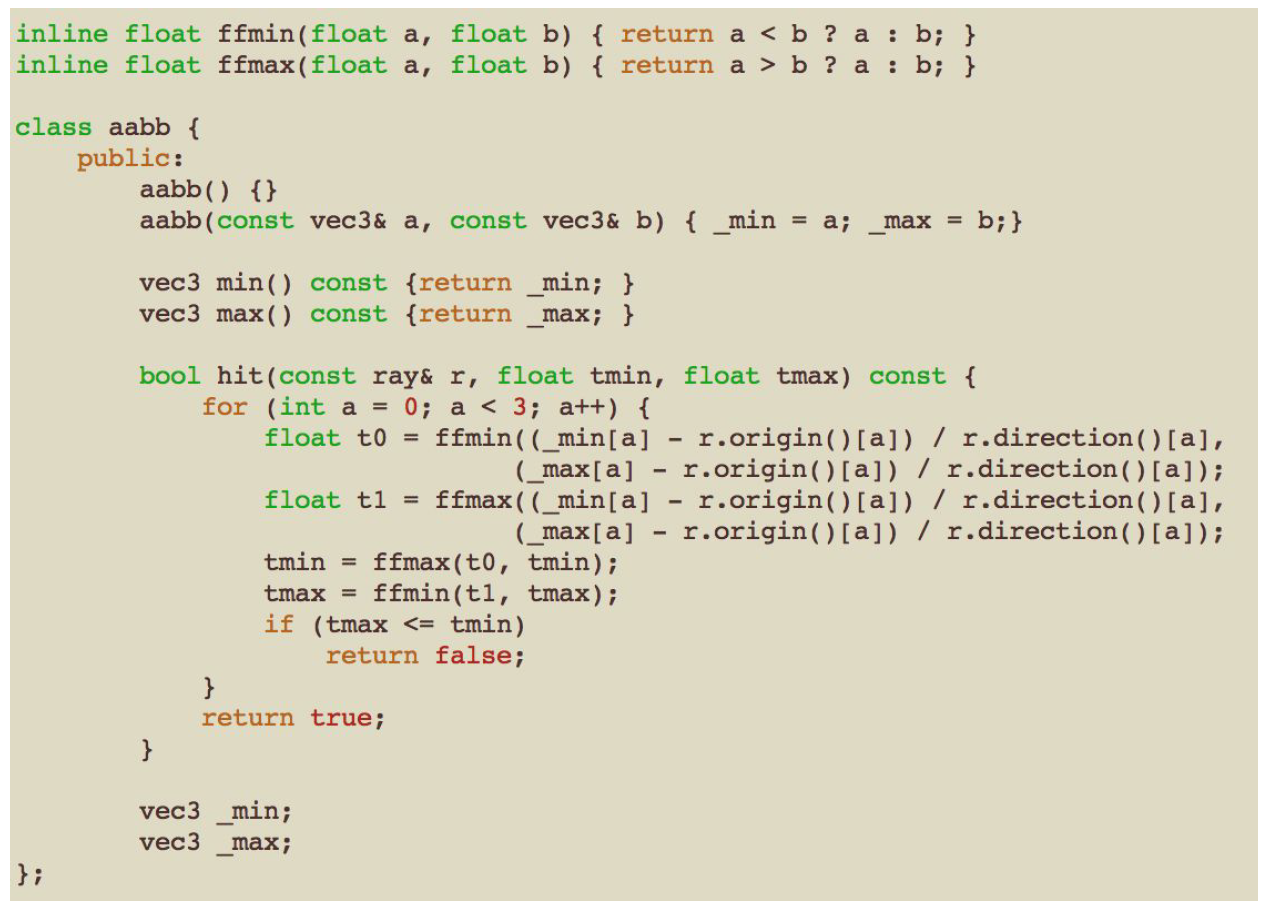
　　注意，内置的fmax()被ffmax()取代，ffmax()速度更快，因为它不需要考虑NaN和其他异常。在回顾这个相交方法时，皮克斯的安德鲁·肯斯勒做了一些实验，并提出了这个版本的代码，它在很多编译器上都运行得非常好，我把它作为我的首选方法:

　　　　

 

　　我们现在需要添加一个函数来计算所有hitable的边界框。 然后我们将在所有图元上创建一个框的层次结构，并且各个图元（如球体）将存在于各个叶子上。 该函数返回bool，因为并非所有图元都具有边界框（例如，无限平面）。 此外，对象移动，因此帧的间隔需要time1和time2，并且边界框将绑定在该间隔内移动的对象。

　开始针对各个图元设计包围体

　　　　

　　对于球体，包围盒函数很简单：

　　　　

　　对于移动球体，我们可以取球体在t0处的盒子，以及球体在t1处的盒子，然后计算这两个盒子的盒子:

　　　　

　　对于列表，您可以在构造时存储边界框，或者动态地计算它。我喜欢动态计算，因为它通常只在BVH结构中调用。

　　　　

　　这需要为aabb提供包围盒函数，该函数计算两个盒子的边界框。

 　　　　

　　BVH也将成为一个可继承的 - 就像hitable列表一样。 它实际上是一个容器，但它可以响应查询“这条光线击中了你吗？”。 一个设计问题是我们是否有两个类，一个用于树，一个用于树中的节点; 或者我们只有一个类，并且根只是我们指向的节点。 在可行的情况下，我是一流设计的粉丝。 所以这是一个类：

　　　　

　　请注意，子指针是通用的hitable。 它们可以是其他bvh_notes，或球体，或任何其他hitable。

　　hit函数非常简单:检查节点的方框是否被击中，如果被击中，检查子节点并整理细节:

　　　　

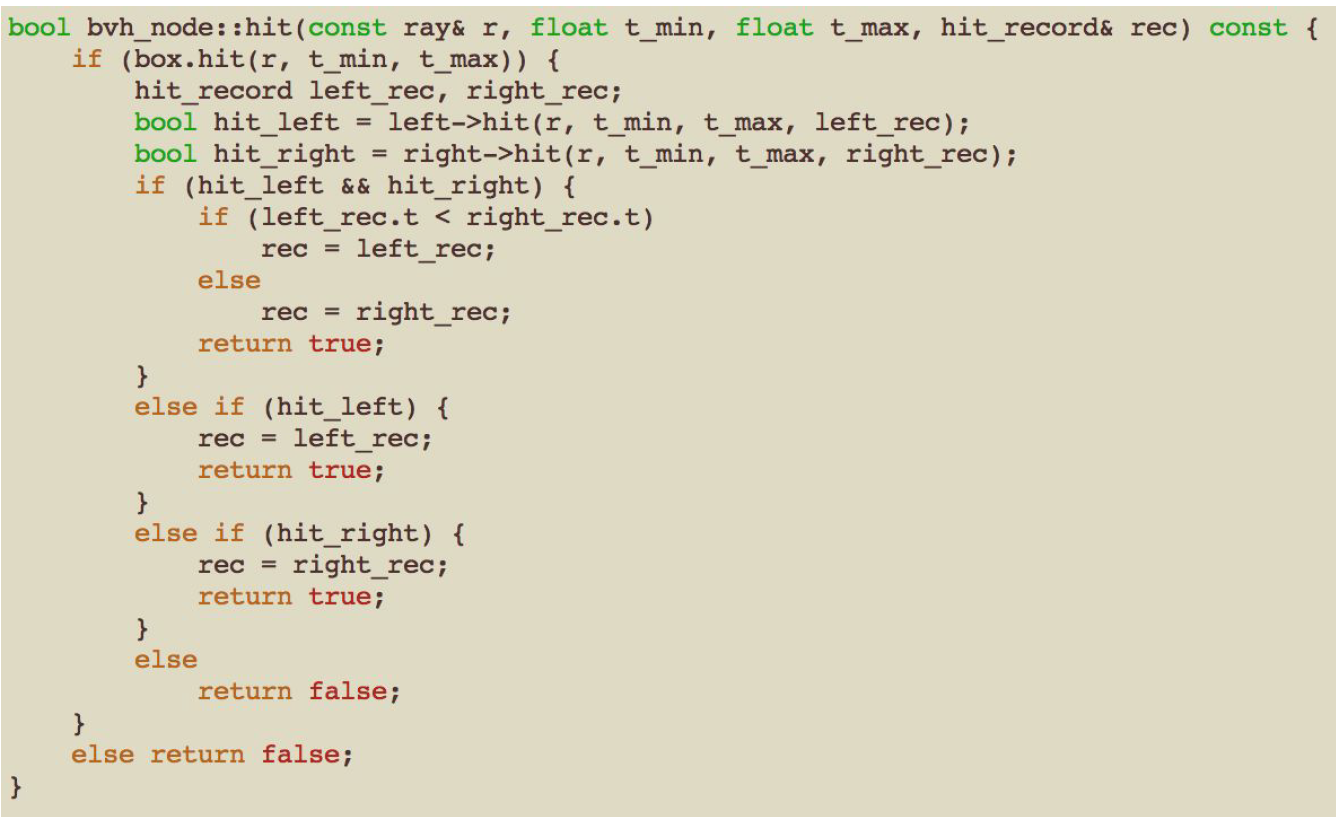
　　任何效率结构中最复杂的部分，包括BVH，都是构建它。我们在构造函数中这样做。BVH的一个好处是，只要bvh_node中的对象列表被划分为两个子列表，hit函数就可以工作。如果分割做得很好，那么它将会工作得最好，这样两个子节点的边界框就会比他们父母的边界框小，但这是为了速度而不是正确性。我将选择中间地带，在每个节点上沿着一个轴分割列表。我将为简单起见:　　

　　　　1)随机选择一个轴

　　　　2)使用库qsort对图元进行排序。

　　　　3)在每一个子树中各放一半

　　我使用的是老式的C qsort而不是c++排序，因为我需要根据轴使用不同的比较运算符，qsort使用一个比较函数，而不是使用小于运算符。我传入一个指向指针的指针——这只是指向“指针数组”的C，因为C中的指针也可以是指向数组第一个元素的指针。当列表是两个元素时，我在每个子树中放入一个元素并结束递归。遍历算法应该是平滑的，不需要检查空指针，所以如果我只有一个元素，我就在每个子树中复制它。显式地检查三个元素并只执行一个递归可能会有一点帮助，但我认为整个方法稍后将得到优化。这个收益率:

　　　　

　　检查是否有一个边界框，以防你输入一个没有边界框的无限大平面。我们没有这些图元，所以不应该在添加这些原语支持之前发生。

　　比较函数必须接受您所释放的空指针。这是老派的C，它提醒我为什么要发明c++。我得把它弄得一团糟才能把所有的指针都弄对。如果你喜欢这一部分，你有一个作为一个系统人的未来!