【学习笔记】连通性相关
强连通分量定义
强连通是指在有向图中任意两节点 \(u,v\) 可相互到达,我们称 \(u,v\) 两点强连通。
强连通分量(Strongly Connected Compoments,SCC)是指极大的强连通子图。
如何求强连通分量
-
算法一:Tarjan
最常用的就是 Tarjan 算法。
前置算法:DFS 生成树。
顾名思义,DFS 生成树即为通过对图的深度优先遍历得到的由遍历顺序决定的树。
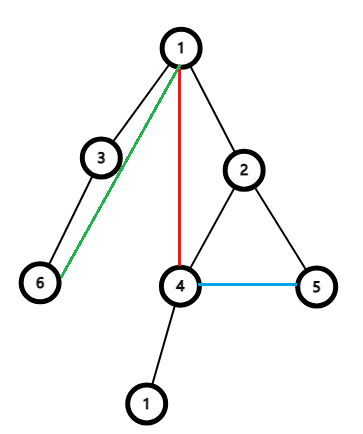
这是一棵 DFS 生成树,其中有几种边:
- 黑色:树边,即为 DFS 遍历过程中遍历到未遍历的点产生的边。
- 蓝色:横插边,DFS 遍历中遇到了已遍历的节点,但此点并非当前点祖先。
- 红色:返祖边,DFS 遍历过程中遍历到了已经访问过的祖先节点。
- 绿色:前向边,DFS 遍历过程中由子树根节点向子树内节点遍历时产生的边。
可以证明,对于强连通分量中的两点 \(u,v\),假设 \(u\) 在 DFS 生成树上第一个被遍历到,那么 \(v\) 一定在 \(u\) 的子树内,即 \(u\) 可以视作这个强连通分量的根。
Tarjan 就是 DFS,每次将当前点的子树视作一个强连通分量,将没有处理的过的子树中的节点压入栈里。
我们会维护以下变量:
- \(dfn_u\):DFS 遍历到 \(u\) 的次序。
- \(low_u\):从 \(u\) 的子树能够回溯到的最早在栈中的节点,可以理解为从 \(u\) 的子树中通过一条不存在于搜索树上的边能到达的点。
- 栈 \(stk\):存储未处理过的节点。
- \(vis_u\):当前 \(u\) 节点是否访问过。
同时还有一个性质:DFS 生成树中,子树根节点 \(u\) 的 \(dfn_u\) 一定是比子节点 \(v\) 的 \(dfn_v\) 小的。
概括一下:DFS 生成树上从根节点出发的一条路径上的 \(dfn\) 单增,\(low\) 严格非降。
切入正题。
我们在深搜过程中维护 \(dfn_u,low_u\),有以下更新:
- 如果说 \(v\) 访问过,更新 \(low_u \leftarrow \min\{low_u,dfn_v\}\)。
- 如果说 \(v\) 未被访问,再向下继续搜,更新 \(low_u \leftarrow \min\{low_u,low_v\}\)。
接下来考虑如何判断强连通分量的根。
不难发现当前节点子树(包括根)可以回溯到的 \(low_u = dfn_u\) 并且 \(u\) 被访问过且在栈中,说明 \(u\) 是强连通分量中第一个在 DFS 生成树上被遍历到的点,由此我们就将栈中存的所有在 \(u\) 之后入栈的点找到,这些点就构成了一个强连通分量。
代码实现长这样:
void tarjan (int u) { dfn[u] = low[u] = ++ ind; stk[++ top] = u, inStk[u] = 1; // 打标记入栈 for (int i = head[u]; ~i; i = edge[i].nxt) { int v = edge[i].v; if (!dfn[v]) { // 未访问过 tarjan (v); low[u] = min (low[u], low[v]); // 更新low } else if (inStk[v]) { low[u] = min (low[u], dfn[v]); // 访问过 } } if (!(dfn[u] ^ low[u])) { // 找到 SCC 的根了 sccnt ++; while (stk[top + 1] ^ u) { // 弹出 SCC 中的节点 inStk[stk[top]] = 0; Col[stk[top --]] = sccnt; // 标记每个点属于哪个 SCC } } } -
算法二:Kosaraju
不是很常用,但很好理解。
具体过程是两次 DFS,需要建出原图和原图的反图。
第一次在原图上 DFS 在回溯前给当前点打上编号,第二次在反图上 DFS 从编号最大的点开始,如果说当前点没有被标记为在强连通分量中,从当前点开始遍历,找到与之联通的极大点集,这就是一个强连通分量。
代码实现长这样:
void dfs1 (int u) { vis[u] = 1; for (int i = Head[u]; ~i; i = Edge[i].nxt) { int v = Edge[i].v; dfs1 (v); } Vec.push_back (u); // 回溯之前编号 } void dfs2 (int u) { Col[u] = sccnt; // 标记属于哪个 SCC for (int i = _Head[u]; ~i; i = _Edge[i].nxt) { int v = _Edge[i].v; dfs2 (v); } } void Kosaraju() { for (int i = 1; i <= n; i ++) { if (!vis[i]) dfs1 (i); } for (int i = n; i; i --) { if (!Col[Vec[i]]) { // 没有访问过 sccnt ++; dfs2 (Vec[i]); } } }
Ex.1 P3387 【模板】缩点
缩点之后建出新图,在新图上跑 spfa 求最长路,缩点同时统计强连通分量中的点权和。
#include <bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MAXN = 2e5 + 33;
int n, m, A[MAXN], head[MAXN], idx, From[MAXN], To[MAXN], new_head[MAXN], Ans, Sum[MAXN];
struct Edge {
int v, nxt;
Edge (int v = 0, int nxt = 0):v(v), nxt(nxt){};
} edge[MAXN], new_edge[MAXN];
inline void Addedge (Edge *edge, int *head, int u, int v) { edge[++ idx] = Edge (v, head[u]), head[u] = idx; }
namespace Tarjan {
int dfn[MAXN], low[MAXN], sccnt, Col[MAXN], stk[MAXN], top, ind;
bool inStk[MAXN];
void tarjan (int u) {
dfn[u] = low[u] = ++ ind;
stk[++ top] = u, inStk[u] = 1;
for (int i = head[u]; ~i; i = edge[i].nxt) {
int v = edge[i].v;
if (!dfn[v]) {
tarjan (v);
low[u] = min (low[u], low[v]);
} else if (inStk[v]) {
low[u] = min (low[u], dfn[v]);
}
}
if (!(dfn[u] ^ low[u])) {
sccnt ++;
while (stk[top + 1] ^ u) {
inStk[stk[top]] = 0;
Sum[sccnt] += A[stk[top]];
Col[stk[top --]] = sccnt;
}
}
}
} using namespace Tarjan;
namespace Spfa {
int Dis[MAXN]; bool vis[MAXN];
queue <int> q;
inline void initDis() { memset (Dis, -0x3f, sizeof (Dis)); }
inline void spfa (int s) {
initDis(), q.push (s);
Dis[s] = Sum[s], vis[s] = 1;
while (!q.empty()) {
int u = q.front(); q.pop();
vis[u] = 0;
for (int i = new_head[u]; ~i; i = new_edge[i].nxt) {
int v = new_edge[i].v;
if (Dis[v] < Dis[u] + Sum[v]) {
Dis[v] = Dis[u] + Sum[v];
if (!vis[v]) {
vis[v] = 1;
q.push (v);
}
}
}
}
for (int i = 1; i <= sccnt; i ++)
Ans = max (Ans, Dis[i]);
}
} using namespace Spfa;
signed main() {
scanf ("%lld %lld", &n, &m);
memset (head, -1, sizeof (head));
for (int i = 1; i <= n; i ++)
scanf ("%lld", &A[i]);
for (int i = 1; i <= m; i ++) {
scanf ("%lld %lld", &From[i], &To[i]);
Addedge (edge, head, From[i], To[i]);
}
for (int i = 1; i <= n; i ++) {
if (!dfn[i])
tarjan (i);
}
memset (new_head, -1, sizeof (new_head)), idx = 0;
for (int i = 1; i <= m; i ++) {
if (Col[From[i]] ^ Col[To[i]])
Addedge (new_edge, new_head, Col[From[i]], Col[To[i]]);
}
for (int i = 1; i <= sccnt; i ++) spfa (i);
printf ("%lld\n", Ans);
return 0;
}
这里要注意的是:
Tarjan 优先会访问出度为 \(0\) 的点,也就是说最后缩点出来的 DAG 中强连通分量的编号是逆拓扑序。
Ex.2 P7251 [JSOI2014] 强连通图
对于第一个问题,答案就是最大的 \(\text{SCC}\) 的大小。
对于第二个问题,因为选择出度为 \(0\) 的点最后还是会要连入度为 \(0\) 的点,因此反而选择两者之中最大值最优。
#include <bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MAXN = 3e5 + 33;
int n, m, head[MAXN], idx, U[MAXN], V[MAXN];
struct EDGE {
int v, nxt;
EDGE (int v = 0, int nxt = 0):v(v), nxt(nxt){};
} Edge[MAXN << 1];
inline void AddEdge (int u, int v) { Edge[idx] = EDGE (v, head[u]), head[u] = idx ++; }
int dfn[MAXN], low[MAXN], sccnt, Col[MAXN], ind, stk[MAXN], top, Siz[MAXN];
bool inStk[MAXN], In[MAXN], Out[MAXN];
void Tarjan (int u) {
dfn[u] = low[u] = ++ ind;
stk[++ top] = u, inStk[u] = 1;
for (int i = head[u]; ~i; i = Edge[i].nxt) {
int v = Edge[i].v;
if (!dfn[v]) {
Tarjan(v);
low[u] = min (low[u], low[v]);
} else if (inStk[v]) {
low[u] = min (low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
sccnt ++;
while (stk[top + 1] ^ u) {
Siz[sccnt] ++;
Col[stk[top]] = sccnt;
inStk[stk[top --]] = 0;
}
}
}
signed main() {
scanf ("%lld %lld", &n, &m);
memset (head, -1, sizeof (head));
for (int i = 1, u, v; i <= m; i ++) {
scanf ("%lld %lld", &u, &v);
AddEdge (u, v), U[i] = u, V[i] = v;
}
for (int i = 1; i <= n; i ++) {
if (!dfn[i])
Tarjan(i);
}
int Ans1 = 0, Ans2 = 0;
for (int i = 1; i <= sccnt; i ++)
Ans1 = max (Ans1, Siz[i]);
for (int i = 1; i <= m; i ++) {
if (Col[U[i]] ^ Col[V[i]])
In[Col[V[i]]] = Out[Col[U[i]]] = 1;
}
int tot_In = 0, tot_Out = 0;
for (int i = 1; i <= sccnt; i ++) {
if (!In[i]) {
tot_In ++;
} if (!Out[i]) {
tot_Out ++;
}
}
Ans2 = ((sccnt ^ 1) ? max (tot_In, tot_Out) : 0);
printf ("%lld\n%lld\n", Ans1, Ans2);
return 0;
}
双联通分量
双联通分量分为点双联通分量和边双联通分量,注意,以上两个都在无向图中讨论。
以下是一个无向图。
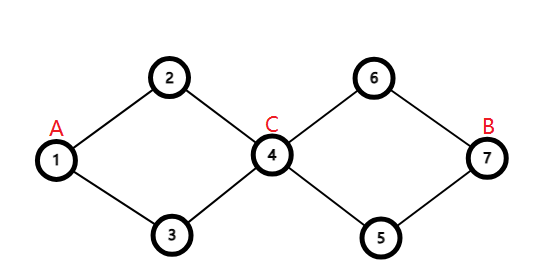
我们来讨论 \(A,B,C\) 三点的双连通性。
-
点双联通
意为对于 \(u,v\) 两点来说,如果任意删除一次图中某个除 \(u,v\) 以外的节点,都不能使得 \(u,v\) 不连通,我们称 \(u,v\) 两点点双联通。
如图,\(A,C\) 两点点双联通,\(B,C\) 两点点双联通,但是 \(A,B\) 两点不点双联通,所以点双联通不具有传递性。
-
点双连通分量
顾名思义,极大的点双联通子图即为一个点双连通分量。
-
边双联通
意为对于 \(u,v\) 两点来说,如果任意删除一次图中某条边,都不能使得 \(u,v\) 不连通,我们称 \(u,v\) 两点边双联通。
如图,\(A,C\) 边双联通,\(B,C\) 边双联通,\(A,B\) 也边双联通,所以边双联通具有传递性。
-
边双联通分量
同上,极大的边双联通子图即为一个边双联通分量。
割点和割边
以下均在无向图中讨论。
-
割点
如果说你删除了一个点,使得该图的联通分量增加了,那么删除的这个点就是割点。
-
割边
同理,如果说你删除了一条边,使得该图的连通分量增加了,那么删除的这条边就是割边,又称桥。
如何求割点
求割点的过程就体现了 Tarjan 算法在连通性问题中的通用性。
如下图,给每个点打上时间戳。
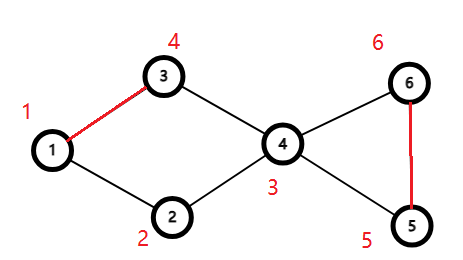
红色的边是非树边(不在 DFS 生成树上),容易看出 \(4\) 号点是割点,考虑如何求。
首先我们明确一点,Tarjan 中我们会维护 \(dfn_u,low_u\),分别表示 \(u\) 访问的时间戳以及 \(u\) 能回到的最早的祖先节点(不经过父亲),因此如果说 \(low_v \geq dfn_u\),意为子节点无法回到祖先,且最多回到父亲,那么该节点可能成为割点。
为什么是可能呢?
实际上我们要考虑的就是搜索起始点,即子树的根的特殊情况。
- 如果说根节点不是割点,那么砍掉这个点其它的节点依旧能够相互到达,意为根节点的子树大小为 \(1\)。
- 如果说根节点是割点,那么可得根节点的子树大小为 \(2\) 或更大。
代码长这样:
void Tarjan (int u, int fa) {
dfn[u] = low[u] = ++ ind;
inStk[u] = 1;
int SonCnt = 0;
for (int i = head[u]; ~i; i = edge[i].nxt) {
int v = edge[i].v;
if (!inStk[v]) {
SonCnt ++; // 记录子节点个数
Tarjan (v, u);
low[u] = min (low[u], low[v]);
if (low[v] >= dfn[u] && (u ^ fa) && !isNode[u]) // 如果说不是自己且满足割点的条件且没有被标记过
isNode[u] = 1, NodeCnt ++;
} else if (v ^ fa) {
low[u] = min (low[u], dfn[v]);
}
}
if (u == fa && SonCnt >= 2 && !isNode[u]) // 如果是自己且子树大小 >= 2 且没有被标记过
isNode[u] = 1, NodeCnt ++;
}
如何求割边(桥)
如下图。
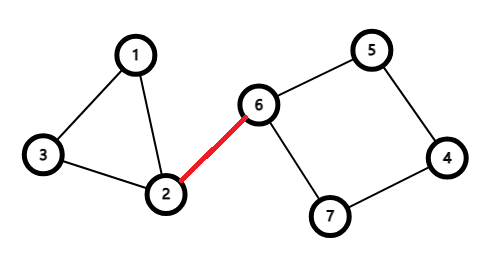
红色的边为割边。
同理,如果 \(low_v > dfn_u\) 意为子节点回不到祖先节点(包括父亲),那么连接 \((u,v)\) 的这条边就是割边。
代码长这样:
void Tarjan (int u, int fa) {
dfn[u] = low[u] = ++ ind;
for (int i = Head[u]; ~i; i = Edge[i].nxt) {
int v = Edge[i].v;
if (!dfn[v]) {
Tarjan (v, u);
low[u] = min (low[u], low[v]);
if (low[v] > dfn[u])
isBridge[i] = 1, cnt ++;
} else if (v ^ fa) {
low[u] = min (low[u], dfn[v]);
}
}
}
上述情况仅限于图中无重边的情况,有重边该怎么办呢?
你会发现只需要打一个标记即可。
代码长这样:
void Tarjan (int u, int fa) {
bool flag = false;
dfn[u] = low[u] = ++ ind;
for (int i = Head[u]; ~i; i = Edge[i].nxt) {
int v = Edge[i].v;
if (!dfn[v]) {
Tarjan (v, u);
low[u] = min (low[u], low[v]);
if (low[v] > dfn[u])
isBridge[i] = 1, cnt ++;
} else {
if (v ^ fa || !flag) {
low[u] = min (low[u], dfn[v]);
} else {
flag = true;
}
}
}
}
如何求双联通分量
前置知识就是割点和割边。
-
点双联通分量
有如下性质:
- 两个点双有且仅有一个公共点,且该点为割点。
- 点双在 DFS 生成树上时间戳最小的节点一定是根或割点。
对于第二个性质分情况:
-
该点为割点,则其定为点双的根。
-
该点为根节点:
- 子树大小为 \(0\),将其自视作一个点双。
- 仅有一棵子树,则该点就是树的根。
- 拥有两棵及以上子树,则该点就是割点。
代码长这样:
void Tarjan (int u, int fa) { dfn[u] = low[u] = ++ ind; stk[++ top] = u, inStk[u] = 1; int SonCnt = 0; for (int i = head[u]; ~i; i = edge[i].nxt) { int v = edge[i].v; if (!inStk[v]) { SonCnt ++; Tarjan (v, u); low[u] = min (low[u], low[v]); if (low[v] >= dfn[u]) { // 如果是割点 Sccnt ++; while (stk[top + 1] != v) Node[Sccnt].push_back (stk[top --]); Node[Sccnt].push_back (u); } } else if (v ^ fa) { low[u] = min (low[u], dfn[v]); } } if (!fa && !SonCnt) // 自己是割点 Node[++ Sccnt].push_back (u); } -
边双联通分量
-
算法一
我们先求出所有的割边,即可使用 DFS 找到所有边双。
-
算法二
你会发现边双对应的就是无向图中的强连通分量,因为无向图的 DFS 生成树中,边双中的节点在同一子树,当然需要判是否为回边。
代码长这样:
void Tarjan (int u, int lst) { dfn[u] = low[u] = ++ ind; stk[++ top] = u, inStk[u] = 1; for (int i = head[u]; ~i; i = edge[i].nxt) { int v = edge[i].v; if (i == (lst ^ 1)) continue; if (!dfn[v]) { Tarjan (v, i); low[u] = min (low[u], low[v]); } else if (inStk[v]) { low[u] = min (low[u], dfn[v]); } } if (dfn[u] == low[u]) { sccnt ++; while (stk[top + 1] ^ u) { Nod[sccnt].push_back (stk[top]); inStk[stk[top --]] = 0; } } }
-
例题
Ex.1 P4742 [Wind Festival] Running In The Sky
这题有环,有向图中的环就是一个强连通分量,所以我们可以用 Tarjan 缩点建新图,在新图上拓扑序 dp。
分别用两个 dp 数组维护路径最大亮度和最长路。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 5e5 + 10;
int n, m, K[MAXN], Head[MAXN], idx, newHead[MAXN], newidx;
struct DAG {
int v, nxt;
DAG (int v = 0, int nxt = 0):v(v), nxt(nxt){};
} Edge[MAXN], newEdge[MAXN];
inline void AddEdge (int u, int v) { Edge[++ idx] = DAG (v, Head[u]), Head[u] = idx; }
inline void newAddEdge (int u, int v) { newEdge[++ newidx] = DAG (v, newHead[u]), newHead[u] = newidx; }
int dfn[MAXN], low[MAXN], sccnt, Col[MAXN], stk[MAXN], top, ind, sumVal[MAXN], maxVal[MAXN];
bool vis[MAXN];
void Tarjan (int u) {
dfn[u] = low[u] = ++ ind;
stk[++ top] = u, vis[u] = 1;
for (int i = Head[u]; ~i; i = Edge[i].nxt) {
int v = Edge[i].v;
if (!dfn[v]) {
Tarjan (v);
low[u] = min (low[u], low[v]);
} else if (vis[v]) {
low[u] = min (low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
sccnt ++;
while (stk[top + 1] ^ u) {
Col[stk[top]] = sccnt;
sumVal[sccnt] += K[stk[top]];
maxVal[sccnt] = max (maxVal[sccnt], K[stk[top]]);
vis[stk[top --]] = 0;
}
}
}
int dpSum[MAXN], _u[MAXN], _v[MAXN], in[MAXN], dpMax[MAXN];
inline void tpsort() {
queue <int> q;
for (int i = 1; i <= sccnt; i ++) {
if (!in[i]) q.push (i);
dpSum[i] = sumVal[i], dpMax[i] = maxVal[i];
}
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = newHead[u]; ~i; i = newEdge[i].nxt) {
int v = newEdge[i].v;
if (!(-- in[v])) q.push (v);
if (dpSum[v] < dpSum[u] + sumVal[v]) {
dpSum[v] = dpSum[u] + sumVal[v];
dpMax[v] = max (dpMax[u], maxVal[v]);
} else if (dpSum[v] == dpSum[u] + sumVal[v]) {
dpMax[v] = max (dpMax[v], dpMax[u]);
}
}
}
}
signed main() {
scanf ("%lld %lld", &n, &m);
memset (Head, -1, sizeof (Head));
memset (newHead, -1, sizeof (newHead));
memset (maxVal, -1, sizeof (maxVal));
memset (dpSum, -0x3f, sizeof (dpSum));
memset (dpMax, -1, sizeof (dpMax));
for (int i = 1; i <= n; i ++)
scanf ("%lld", &K[i]);
for (int i = 1, u, v; i <= m; i ++) {
scanf ("%lld %lld", &u, &v);
AddEdge (u, v);
_u[i] = u, _v[i] = v;
}
for (int i = 1; i <= n; i ++) {
if (!dfn[i]) Tarjan (i);
}
for (int u = 1; u <= n; u ++) {
for (int i = Head[u]; ~i; i = Edge[i].nxt) {
int v = Edge[i].v;
if (Col[u] ^ Col[v])
newAddEdge (Col[u], Col[v]), in[Col[v]] ++;
}
}
tpsort();
int Ans = 1;
for (int i = 2; i <= sccnt; i ++) {
if (dpSum[i] > dpSum[Ans] || (dpSum[i] == dpSum[Ans] && dpMax[i] > dpMax[Ans])) Ans = i;
}
printf ("%lld %lld\n", dpSum[Ans], dpMax[Ans]);
return 0;
}
Ex.2 P5058 [ZJOI2004] 嗅探器
我们要找能够隔开 \(A,B\) 的割点,将问题放到搜索树上。
首先明确一点,如果说 \(v\) 在 \(u\) 的子树内,应满足 \(dfn_v \leq dfn_u\),利用这一点,我们就去找既是割点又满足 \(dfn_x \leq dfn_A \text{ and } dfn_x >dfn_B\) 或者 \(dfn_x \leq dfn_B \text{ and } dfn_x >dfn_A\) 的最小编号的点。
#include <bits/stdc++.h>
#define int long long
using namespace std;
constexpr int MAXN = 5e5 + 10;
int n, A, B, Head[MAXN], idx;
struct Graph {
int v, nxt;
Graph (int v = 0, int nxt = 0):v(v), nxt(nxt){};
} Edge[MAXN];
inline void AddEdge (int u, int v) { Edge[idx] = Graph (v, Head[u]), Head[u] = idx ++; }
inline void readin() {
scanf ("%lld", &n);
memset (Head, -1, sizeof (Head));
while (true) {
int u, v;
scanf ("%lld %lld", &u, &v);
if (!u && !v) break;
AddEdge (u, v), AddEdge (v, u);
}
scanf ("%lld %lld", &A, &B);
}
int dfn[MAXN], low[MAXN], ind, Ans = 0x7f7f7f7f;
inline bool Chk_inTree (int u) {
if (dfn[u] <= dfn[A] && dfn[u] > dfn[B]) return true;
if (dfn[u] <= dfn[B] && dfn[u] > dfn[A]) return true;
return false;
}
void Tarjan (int u, int fa) {
dfn[u] = low[u] = ++ ind;
for (int i = Head[u]; ~i; i = Edge[i].nxt) {
int v = Edge[i].v;
if (!dfn[v]) {
Tarjan (v, u);
low[u] = min (low[u], low[v]);
if (low[v] >= dfn[u] && u ^ A && u ^ B && Chk_inTree (u)) Ans = min (Ans, u);
} else if (v ^ fa) {
low[u] = min (low[u], dfn[v]);
}
}
}
inline void Work() {
Tarjan (1, 0);
if (Ans == 0x7f7f7f7f) {
printf ("No solution\n");
} else {
printf ("%lld\n", Ans);
}
}
signed main() {
readin();
Work();
return 0;
}
Ex.3 P2272 [ZJOI2007] 最大半连通子图
原图有环,所以缩点建新图。
根据最大半联通子图的定义,我们推出其实就是要求一个最长链,所以拓扑序 dp 即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
int res = 0, f = 1;
char ch = getchar();
while (!isdigit(ch)) f = ch == '-' ? -1 : 1, ch = getchar();
while (isdigit(ch)) res = (res << 1) + (res << 3) + (ch ^ 48), ch = getchar();
return res * f;
}
const int MAXN = 1e6 + 10;
int n, m, mod, Head[MAXN], idx, newHead[MAXN], newidx;
struct DAG {
int v, nxt;
DAG (int v = 0, int nxt = 0):v(v), nxt(nxt){};
} Edge[MAXN], newEdge[MAXN];
inline void AddEdge (int u, int v) { Edge[++ idx] = DAG (v, Head[u]), Head[u] = idx; }
inline void newAddEdge (int u, int v) { newEdge[++ newidx] = DAG (v, newHead[u]), newHead[u] = newidx; }
int dfn[MAXN], low[MAXN], stk[MAXN], Siz[MAXN], Col[MAXN], sccnt, top, ind;
bool vis[MAXN];
void Tarjan (int u) {
dfn[u] = low[u] = ++ ind;
stk[++ top] = u, vis[u] = 1;
for (int i = Head[u]; ~i; i = Edge[i].nxt) {
int v = Edge[i].v;
if (!dfn[v]) {
Tarjan (v);
low[u] = min (low[u], low[v]);
} else if (vis[v]) {
low[u] = min (low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
sccnt ++;
while (stk[top + 1] ^ u) {
Col[stk[top]] = sccnt;
Siz[sccnt] ++;
vis[stk[top --]] = 0;
}
}
}
int dpSiz[MAXN], dpCnt[MAXN], in[MAXN], tag[MAXN];
inline void tpSort() {
for (int i = sccnt; i; i --)
dpSiz[i] = Siz[i], dpCnt[i] = 1;
for (int u = sccnt; u; u --) {
for (int i = newHead[u]; ~i; i = newEdge[i].nxt) {
int v = newEdge[i].v;
if (tag[v] == u) continue;
tag[v] = u;
if (dpSiz[v] < dpSiz[u] + Siz[v]) {
dpSiz[v] = dpSiz[u] + Siz[v];
dpCnt[v] = dpCnt[u];
} else if (dpSiz[v] == dpSiz[u] + Siz[v]) {
dpCnt[v] = (dpCnt[v] + dpCnt[u]) % mod;
}
}
}
}
signed main() {
n = read(), m = read(), mod = read();
memset (Head, -1, sizeof (Head));
memset (newHead, -1, sizeof (newHead));
for (int i = 1; i <= m; i ++) {
int u = read(), v = read();
AddEdge (u, v);
}
for (int i = 1; i <= n; i ++) {
if (!dfn[i]) Tarjan (i);
}
for (int u = 1; u <= n; u ++) {
for (int i = Head[u]; ~i; i = Edge[i].nxt) {
int v = Edge[i].v;
if (Col[u] ^ Col[v]) {
newAddEdge (Col[u], Col[v]);
in[Col[v]] ++;
}
}
}
tpSort();
int AnsSiz = 0, AnsCnt = 0;
for (int i = 1; i <= sccnt; i ++) {
if (dpSiz[i] > AnsSiz) {
AnsSiz = dpSiz[i], AnsCnt = dpCnt[i];
} else if (dpSiz[i] == AnsSiz) {
AnsCnt = (AnsCnt + dpCnt[i]) % mod;
}
}
printf ("%lld\n%lld\n", AnsSiz, AnsCnt);
return 0;
}
结语
qwq。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号