Hall 定理

Hall 定理

定理内容

在二分图 $ G = (U, V, E) $ 中，存在一个匹配覆盖 \(U\) 的所有顶点（即存在 \(U\) 到 \(V\) 的完美匹配） 当且仅当 对 \(U\) 的任意子集 \(S\)，Hall 条件 $ |N(S)| \ge |S| $ 成立。

充分性

对于任意 \(S\) 有一个完全匹配，那么显然有 $ |N(S)| \ge |S| $。

必要性

利用反证法。

当 Hall 条件成立时，是否有完备匹配。

选择一个最大匹配 \(M\)。

反证：假设其不是一个完备匹配。

因为假设了了 \(M\) 不是一个完备匹配。则必定有一个 \(u \in U\) 使得在 \(V\) 中没有匹配。在下面我们称之为 \(M-不饱和点\)。

现在我们继续定义 \(M-交错路\) 为我们在 \(M\) 这个匹配中通过交替走选择了的边和没有选择的边走出的路径。

定义有集合 \(A = \{E 中所有能通过从 u 出发走 M-交错路 能走到的点\}\)。

设 \(S = A \cap U, T = A \cap V\)。

引理1

\(\forall v\in N(\{u\})，v为M-饱和点\)。

显然，否则可以通过加入 \(u \rightarrow v\) 这条边使得匹配变得更大，与 \(M\) 是最大匹配不符。

引理2

\(S - \{u\}\) 与 \(T\) 应为一一对应的关系。

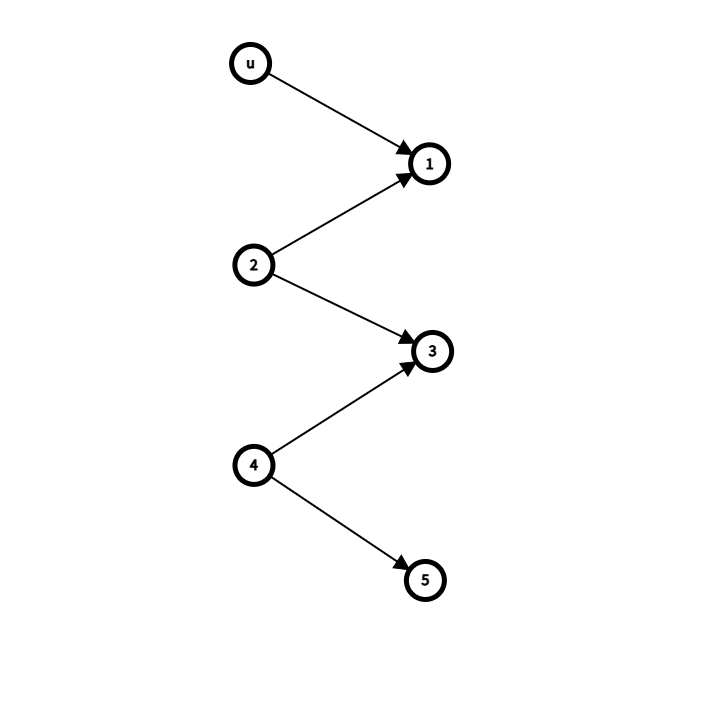
考虑此图：\(S=\{2,4\}\)，\(T=\{1,3,5\}\)（其他不是的情况依旧属于上图情况的并集）。此时并不是一一对应的关系。那么我们可以构造出更大的 \(M\)，与 \(M\) 是最大匹配不符。

从此，我们可以推出 \(|S|=|T|+1\)。

引理3

\(N(S)=T\)。

证明

若存在 \(v \in N(S)\) 且 \(v \notin T\)。

则：

1. 若 \(v\) 是 \(u\) 的邻居，则 \(v\) 不可能是 \(M-不饱和点\)

否则可以存在更大的匹配，矛盾。

2. \(v\) 不能是 \(M-饱和点\)

因为若 \(v\) 是 \(M-饱和点\)，则 \(v\) 一定可以通过 \(M-交错路\) 加入 \(A\) 中，矛盾。

3. \(v\) 不能是 \(S-\{u\}\) 中邻居中的 \(M-不饱和点\)

若是这样，我们就找到了从 \(u\) 出发，\(v\) 结束的\(M-增长路\)，可以获得一个更大的匹配，与 \(M\) 是最大匹配矛盾。

综上，\(N(S)=T\)。

然后，\(|N(S)|=|T|=|S|-1\)，与条件不符，矛盾，故假设不成立。

Hall定理成立！