4.30 二叉树/递归框架思路todo

1.二叉树的思维模式
1.1 是否可以通过遍历一遍二叉树得到答案？如果可以，用一个traverse函数配合外部变量来实现，<遍历的思维模式>
1.2 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，<分解问题的思维方式>

1.3 需要思考：如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候做？

2 二叉树的框架

快速排序本质是二叉树的前序遍历（先把一个元素排好序，再把剩下的元素排好序）
归并排序本质是二叉树的后序遍历（先排序数组的前半部分，再排序后半部分）

3. 前序，中序和后序（根据递归的位置区分）
   
   前序遍历就是即将进入一个元素的时候，递归进入
   后序遍历就是即将离开一个元素的时候，递归离开
   中序位置是左子树遍历完，开始遍历右子树的时候
   （三个时间点）
   
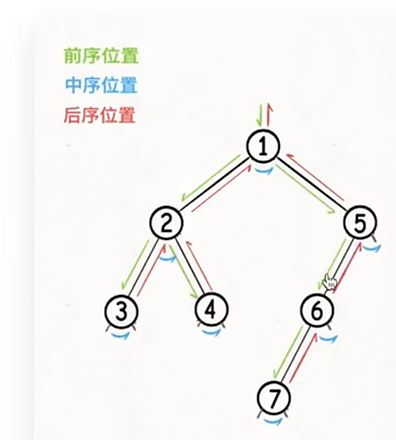
   每一个节点都有属于自己的前中后序位置（多叉树没有，因为叉太多）

4 两种解题思路（回溯算法，动态规划）

例子：二叉树最大深度（前序增加深度，后序减少深度）
分解问题的时候通过函数的功能完成

遍历思路通常函数没有返回值，通过更新外部变量得到结果；（对应回溯法）
而分解问题思路通常有返回值；（对应动态规划）

5。 二叉树的思考过程
（1：是否可以通过遍历一遍二叉树得到结果
（2：是否可以通过递归，分解子树得到结果
（3：需要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做
*前序位置的代码是自顶向下的，后序位置的代码是自下向顶的
前序位置只能从函数参数中获取父节点传来的数据，后序位置代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传回来的数据

一个节点在第几层，你从根节点遍历过来的过程就能顺带记录，用递归函数的参数就能传递下去；而以一个节点为根的整棵子树有多少个节点，你必须遍历完子树之后才能数清楚，然后通过递归函数的返回值拿到答案。
*所以子树问题